Числа Рейнольдса, Фруда, Эйлера, Вебера

Совокупность параметров, определяющих какой-либо гидродинамический процесс, можно рассматривать как конкретное решение дифференциальных уравнений этого процесса. Ему соответствуют вполне определённые начальные и граничные условия. Они представляют собой зависимости или константы, определяющие физические параметры в начальный момент и на границах во время движения. Следовательно, не только уравнения процесса, но также безразмерные формы начальных и граничных условий (условий однозначности) в механически подобных потоках должны быть одинаковыми. Имея это в виду, запишем уравнения Навье-Стокса и приведём их к безразмерному виду, для чего выберем характерные физические параметры L, V, T, P, F0 (если F - cила тяжести, то в качестве F0 удобно взять ускорение g свободного падения) и отнесём к ним соответствующие размерные величины:

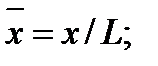
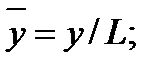
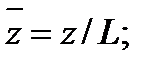
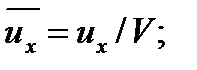
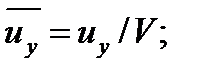
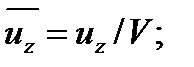
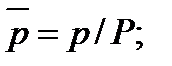
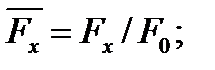
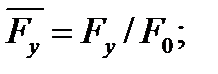
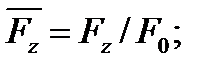
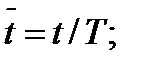
Для плотности и вязкости, которые считаем постоянными, характерные величины не выбираем, так как они сами ими являются. Примем также во внимание размерность дифференциальных операторов и grad:

;

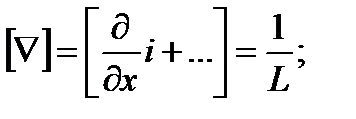
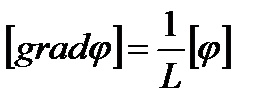Векторное уравнение Навье-Стокса можно представить в виде

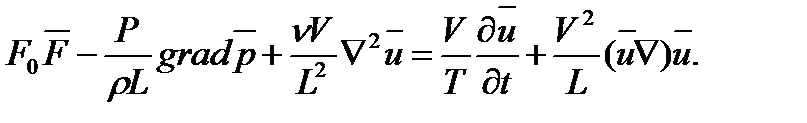(1.48)

Чтобы придать этому уравнению безразмерный вид, разделим все его члены на коэффициент 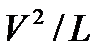при конвективном ускорении. Получим

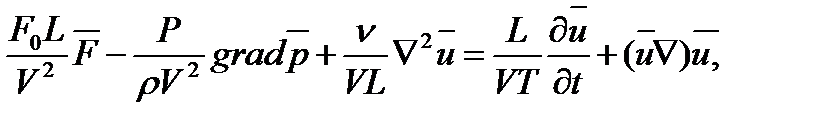(1.49)

где дифференциальные операции выполняются по безразмерным переменным. В этом уравнение все члены, включая комбинации характерных параметров, безразмерны. Для всех динамических подобных потоков оно должно быть одинаковым, а следовательно, группы потоков были одинаковыми, т.е.

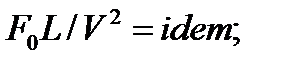
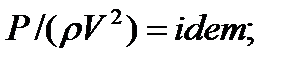
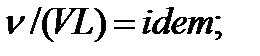
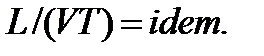(1.50)

Входящие в условия (1.50) безразмерные комплексы играют роль критериев подобия и имеют следующие собственные наименования:

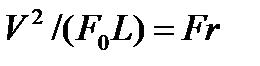- число Фруда; 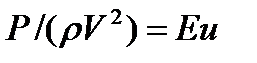- число Эйлера; 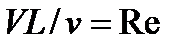- число Рейнольдса; 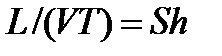- число Струхала.