Уравнение неразрывности
Рассмотрим случай, когда невязкая жидкость течет по горизонтальной цилиндрической трубе с изменяющимся поперечным сечением .
Течение жидкости называют стационарным, если в каждой точке пространства, занимаемого жидкостью, ее скорость с течением времени не изменяется. При стационарном течении через любое поперечное сечение трубы за равные промежутки времени переносятся одинаковые объемы жидкости.
Жидкости практически несжимаемы, т. е. можно считать, что данная масса жидкости всегда имеет неизменный объем. Поэтому одинаковость объемов жидкости, проходящих через разные сечения трубы, означает, что скорость течения жидкости зависит от сечения трубы.
Пусть скорости стационарного течения жидкости через сечения трубы S1 и S2 равны соответственно v1 и v2. Объем жидкости, протекающей за промежуток времени t через сечение S1, равен V1=S1v1t, а объем жидкости, протекающей за то же время через сечение S2, равен V2=S2v2t. Из равенства V1=V2 следует, что
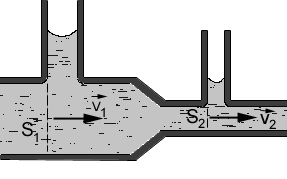 Рис 1.14
Рис 1.14
|
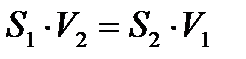 (1.27)
(1.27)
Соотношение (1.27) называют уравнением неразрывности. Из него следует, что 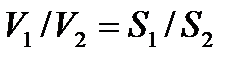 Следовательно, при стационарном течении жидкости скорости движения ее частиц через разные поперечные сечения трубы обратно пропорциональны площадям этих сечений.
Следовательно, при стационарном течении жидкости скорости движения ее частиц через разные поперечные сечения трубы обратно пропорциональны площадям этих сечений.
Поскольку объемный расход Q равен произведению скорости текущей среды V на площадь S поперечного сечения трубки тока, уравнение неразрывности имеет следующий вид:
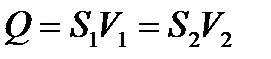 (1.28)
(1.28)
Это уравнение выражает один из основных законов гидроаэромеханики, согласно которому объемный расход во всякой трубке тока, ограниченной соседними линиями тока, должен быть в любой момент времени одинаков во всех ее поперечных сечениях.
Уравнение Бернулли
Основной задачей гидродинамики является изучение законов движения жидкости. Движение жидкости характеризуется скоростями движения частиц и давлением в отдельных точках потока.
Чтобы установить взаимосвязь между основными параметрами движения, а именно между гидродинамическим давлением и скоростью движущейся жидкости, составим уравнения движения жидкости. Эти уравнения могут быть получены из дифференциальных уравнений равновесия жидкости, если к действующим силам согласно принципу д’Аламбера присоединить силы инерции. Получим систему уравнений:
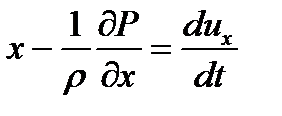
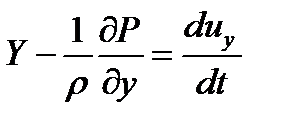 (1.29)
(1.29)
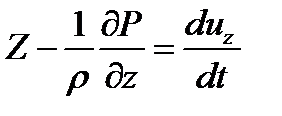
Преобразуем полученные уравнения, применительно к элементарной струйке идеальной жидкости, находящейся в установившемся движении, умножив каждое уравнение соответственно на 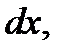
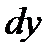 ,
, 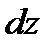 . После по членного суммирования получаем
. После по членного суммирования получаем
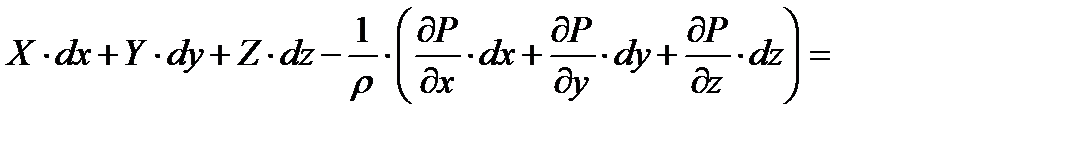
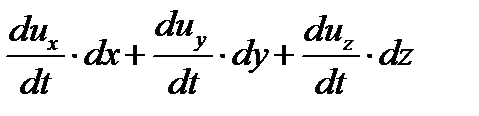 (1.30)
(1.30)
Так как 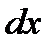 ,
, 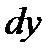 ,
, 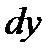 - это проекции элементарного пути, проходимого частицами жидкости за время dt, следовательно:
- это проекции элементарного пути, проходимого частицами жидкости за время dt, следовательно:
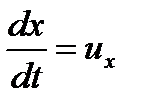
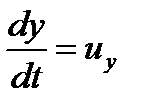
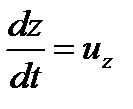 (1.31)
(1.31)
С учетом (3) уравнение (2) примет вид:
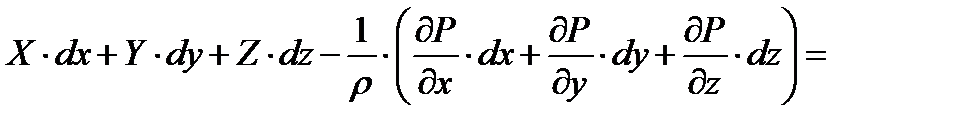
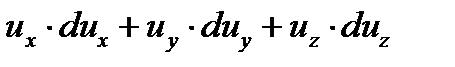 (1.32)
(1.32)
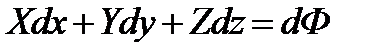 - полный дифференциал силовой функции, выражающей массовые силы, под действием которых осуществляется движение жидкости.
- полный дифференциал силовой функции, выражающей массовые силы, под действием которых осуществляется движение жидкости.
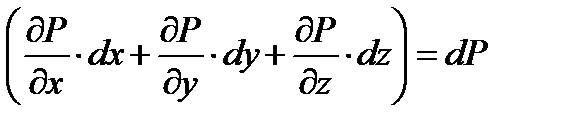 - полный дифференциал давления, так как при установившемся движении гидродинамическое давление не зависит от времени.
- полный дифференциал давления, так как при установившемся движении гидродинамическое давление не зависит от времени.
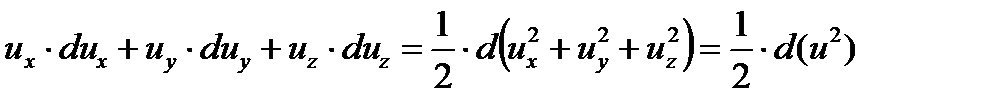 - полный дифференциал скорости, выраженной через ее составляющие по соответствующим осям координат.
- полный дифференциал скорости, выраженной через ее составляющие по соответствующим осям координат.
С учетом вышесказанного уравнение (1.32) примет вид:
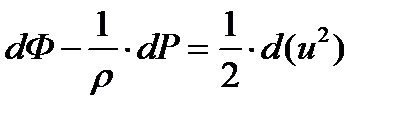 (1.33)
(1.33)
Или окончательно
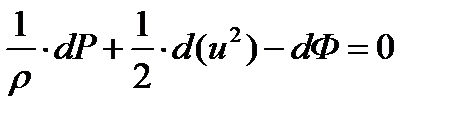 (1.34)
(1.34)
В частном случае, когда из всех массовых сил на движущуюся жидкость действуют только силы тяжести, силовая функция будет равна
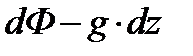 (1.35)
(1.35)
Подставив значение силовой функции в уравнение (6) и проинтегрировав, получим уравнение для рассматриваемого сечения:
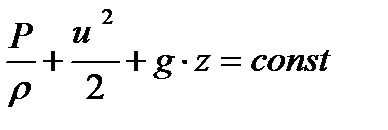 (1.36)
(1.36)
Так как сумма трех членов в уравнении (8) постоянна для любого сечения струйки, то для двух сечений 1 - 1 и 2 - 2 (рис. 1.15) можно записать
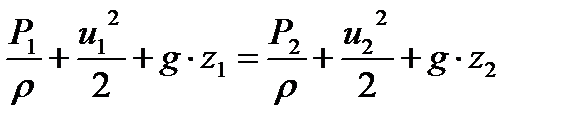 (1.37)
(1.37)
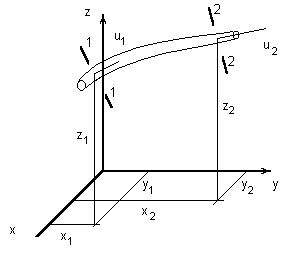 Рис. 1.15 Рис. 1.15
|
Разделив левую и правую часть уравнения (1.37) на g, окончательно получим:
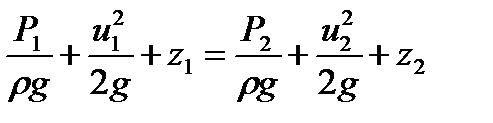 (1.38)
(1.38)
Уравнение (10) устанавливает связь между скоростью движения, давлением и геометрическим положением частиц жидкости для двух сечений струйки и является уравнением Бернулли для элементарной струйки идеальной жидкости.
Дата добавления: 2016-05-28; просмотров: 2801;











