Линии токов жидкости и вихревые линии. Плавно и резко изменяющееся движение

Если в движущейся жидкости взять бесконечно малый замкну­тый контур и через все его точки провести линии тока, то образуется трубчатая поверхность, называемая трубкой тока. Часть потока, заключенная внутри трубки тока, называется элементарной струйкой. При стремлении поперечных размеров струйки к нулю она в пределе стягивается в линию тока.

В любой точке трубки тока, т. е. боковой поверхности струйки, векторы скорости направлены по касательной, а нормальные к этой поверхности составляющие скорости отсутствуют, следовательно, при установившемся движении ни одна частица жидкости, ни в одной точке трубки тока не может проникнуть внутрь струйки или выйти наружу. Трубка тока, таким образом, является как бы непроницае­мой стенкой, а элементарная струйка представляет собой самостоя­тельный элементарный поток.

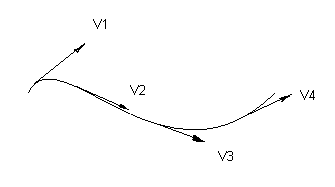
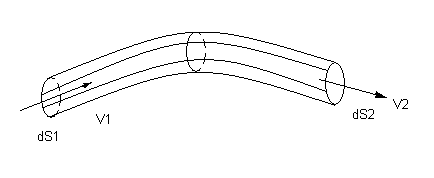
Рис 1.12 Рис 1.3

Линии тока Трубка тока

Потоки конечных размеров будем сначала рассматривать как совокупность элементарных струек, т. е. будем предполагать течение струйным. Из-за различия скоростей соседние струйки будут сколь­зить одна по другой, но не будут перемешиваться одна с другой. Живым сечением, или просто сечением потока, называется в общем случае поверхность в пределах потока, проведенная нормально к ли­ниям тока. Далее будем рассматривать в потоках такие участки, в которых струйки можно считать параллельными и, следовательно, живые сечения — плоскими.

Различают напорные и безнапорные течения жидкости. Напор­ными называют течения в закрытых руслах без свободной поверхно­сти, а безнапорными — течения со свободной поверхностью. При напорных течениях давление вдоль потока обычно переменное, при безнапорном — постоянное (на свободной поверхности) и чаще всего атмосферное. Примерами напорного течения могут служить течения в трубопроводах с повышенным (или пониженным) давлением, в гид­ромашинах или других гидроагрегатах. Безнапорными являются течения в реках, открытых каналах и лотках.

Расходом называется количество жидкости, протекающее через живое течение потока (струйки) в единицу времени. Это количество можно измерить в единицах объёма, в весовых единицах или в единицах массы, в связи с чем различают объёмный Q, весовой Q_G и массовый Q_m расходы.

Для элементарной струйки, имеющий бесконечно малые площади сечений, можно считать истинную скорость одинаковой во всех точках каждого сечения. Следовательно, для этой струйки объёмный(м³/с), весовой(Н/с) и массовый(кг/с) расходы

;

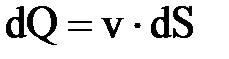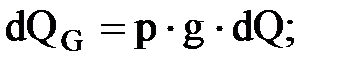
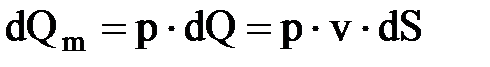
Для потока конечных размеров в общем случае скорость имеет различное значение в разных точках сечения, поэтому расход надо определять как сумму элементарных расходов струек.

Обычно в рассмотрение вводят среднюю по сечению скорость

v_ср =Q/S, откуда Q= v_ср S.

Основываясь на законе сохранения вещества, на предположении о сплошности (неразрывности) течения и на указанном выше свойстве трубки тока, заключающемся в ее «непроницаемости», для устано­вившегося течения несжимаемой жидкости можно утверждать, что объемный расход во всех сечениях элементарной струйки один и тот же:

dQ=v₁dS₁=v₂dS₂=const (вдоль струйки)

Это уравнение называется уравнением объемного расхода для эле­ментарной струйки.

Аналогичное уравнение можно составить и для потока конечных размеров, ограниченного непроницаемыми стенками, только вместо истинных скоростей следует ввести средние скорости.