Сила давления жидкости на плоскую стенку
Используем основное уравнение гидростатики (1.20) для нахождения полной силы давления жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом а (рис. 1.7). Вычислим силу F давления, действующую со стороны жидкости на некоторый участок рассматриваемой стенки, ограниченный произвольным контуром и имеющий площадь, равную S.
Ось 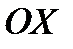 направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось
направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось 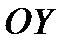 — перпендикулярно к этой линии в плоскости стенки.
— перпендикулярно к этой линии в плоскости стенки.
Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке 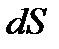 :
:
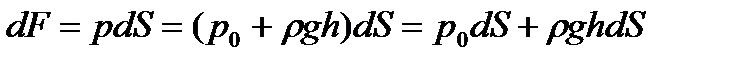
где 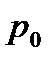 — давление на свободной поверхности;
— давление на свободной поверхности; 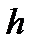 — глубина расположения площадки
— глубина расположения площадки 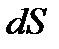 .
.
Для определения полной силы 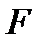 проинтегрируем полученное выражение по всей площади
проинтегрируем полученное выражение по всей площади 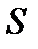 :
:
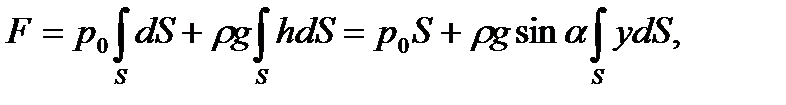
где 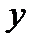 — координата площадки
— координата площадки 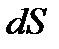 .
.
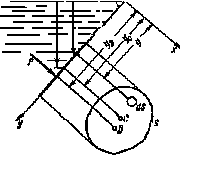
Рис. 1.7
Последний интеграл представляет собой статический момент
площади 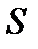 относительно оси
относительно оси 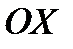 и равен произведению этой площади на координату ее центра тяжести
и равен произведению этой площади на координату ее центра тяжести
(точка С), т. е.
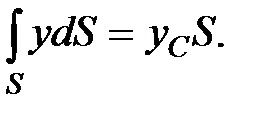
Следовательно,
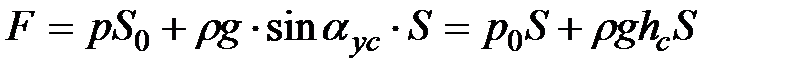
(здесь 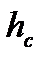 — глубина расположения центра тяжести площади S.),
— глубина расположения центра тяжести площади S.),
или
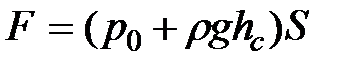 (1.29)
(1.29)
т. е. полная сила давления жидкости на плоскую стенку равна произведению площади стенки на гидростатическое давление 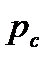 в центре тяжести этойплощади.
в центре тяжести этойплощади.
В частном случае, когда давление Ро 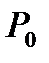 является атмосферным и действует также с другой стороны стенки, сила
является атмосферным и действует также с другой стороны стенки, сила 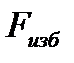 избыточного давления жидкости на плоскую стенку равна лишь силе
избыточного давления жидкости на плоскую стенку равна лишь силе 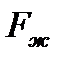 давления от веса жидкости, т. е.
давления от веса жидкости, т. е.
Fизб=F
В общем случае давление 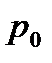 может существенно отличаться от атмосферного, поэтому полную силу
может существенно отличаться от атмосферного, поэтому полную силу 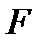 давления жидкости на стенку будем рассматривать как сумму двух сил:
давления жидкости на стенку будем рассматривать как сумму двух сил: 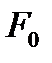 от внешнего давления
от внешнего давления 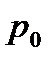 исилы
исилы 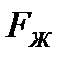 от веса жидкости, т.е.
от веса жидкости, т.е.
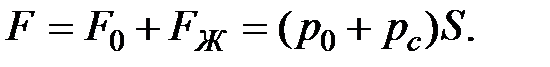
Рассмотрим вопрос о точках приложения этих сил, называемых центрами давления.
Так как внешнее давление 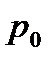 передается всем точкам площади
передается всем точкам площади 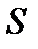 одинаково, то его равнодействующая
одинаково, то его равнодействующая 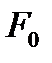 будет приложена в центре тяжести площади
будет приложена в центре тяжести площади 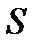 . Для нахождения точки приложения силы давления
. Для нахождения точки приложения силы давления 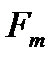 от веса жидкости (точка D) применим теорему механики, согласно которой момент равнодействующей силы относительно оси
от веса жидкости (точка D) применим теорему механики, согласно которой момент равнодействующей силы относительно оси 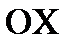 равен сумме моментов составляющих сил, т. е.
равен сумме моментов составляющих сил, т. е.
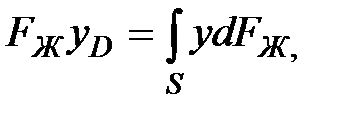
где 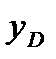 — координата точки приложения силы
— координата точки приложения силы 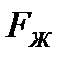 . Выражая
. Выражая 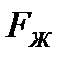 и
и 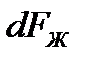 через
через 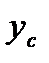 и
и 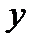 и определяя
и определяя 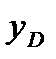 , получаем
, получаем
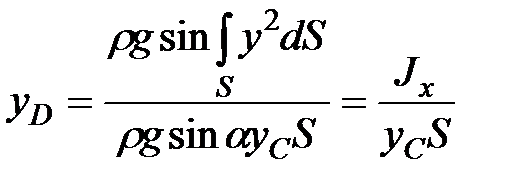
где 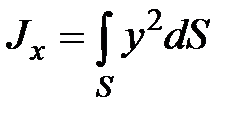 Jx— момент инерции площади
Jx— момент инерции площади 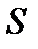 относительно оси
относительно оси 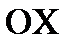 .
.
Учитывая, что
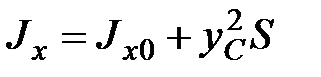
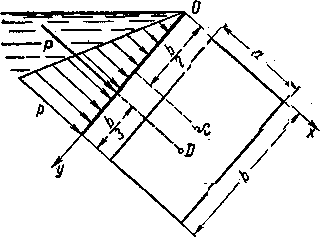
Рис. 1.8 Эпюра давления- жидкости на прямоугольную стенку
(Jx0 — момент инерции площади 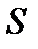 относительно центральной оси, параллельной
относительно центральной оси, параллельной 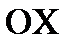 ), находим
), находим
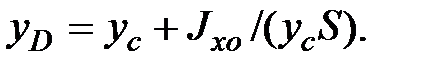 (1.30)
(1.30)
Таким образом, точка приложения силы 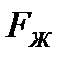 расположена ниже центра тяжести площади стенки; расстояние между ними
расположена ниже центра тяжести площади стенки; расстояние между ними
Если давление 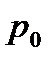 равно атмосферному, то точка D и будет центром давления. При
равно атмосферному, то точка D и будет центром давления. При 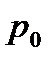 выше атмосферного центр давления находят по правилам механики как точку приложения равнодействующей двух сил: F0 и
выше атмосферного центр давления находят по правилам механики как точку приложения равнодействующей двух сил: F0 и 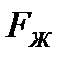 ; чем больше первая сила по сравнению со второй, тем, очевидно, центр давления ближе к центру тяжести площади S.
; чем больше первая сила по сравнению со второй, тем, очевидно, центр давления ближе к центру тяжести площади S.
В частном случае, когда стенка имеет форму прямоугольника размерами, а х b (рис. 1.14) и одна из его сторон, а лежит на свободной поверхности с атмосферным давлением, центр давления D находится на расстоянии b/3 от нижней стороны.
Дата добавления: 2016-05-28; просмотров: 1900;











