РОЗРАХУНОК ГЕОМЕТРИЧНИХ ПАРАМЕТРІВ ЦИЛІНДРИЧНИХ ПРЯМОЗУБИХ ЗУБЧАСТИХ КОЛІС З УМОВИ ВЕРСТАТНОГО ЗАЧЕПЛЕННЯ
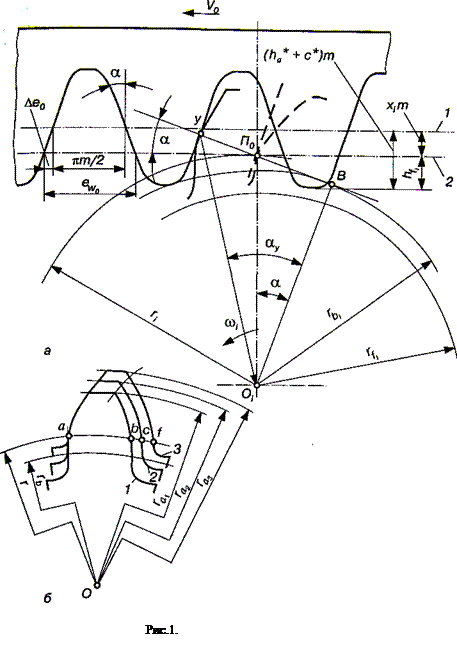 |
Розглянемо зачеплення зубчастого колеса, що нарізується, з прямозубою твірною рейкою, в процесі якого на заготовці формуються зуби відповідної геометрії та розмірів [18]. Картину зачеплення будемо розглядати в торцевому перетині (рис. 9.17, а). У рейковому зачепленні рейка здійснює поступальний рух,
а колесо обертовий. Такі ж рухи повинні виконувати ланки верстатного зачеплення. Необхідну швидкість V0 руху твірної рейки, яка спрямована паралельно ділильній прямій, визначають із співвідношення
Vо =ωiri (1)
де ωi - кутова швидкість заготовки; ri — радіус ділильного кола зубчастого колеса, що нарізується. У цій формулі й далі індекс позначає параметри ріжучого інструменту, а індекс і = 1 або і = 2 - відповідно шестірні або колеса. Індекс і можна опустити, коли його значення неістотне.
Із формули (1) випливає, що при нарізанні зубчастого колеса рейковим інструментом ділильне коло є центроїдою у відносному русі твірного контуру і торцевого перетину заготовки. Інакше кажучи, в процесі нарізання деяка лінія твірного контуру, що дотикається ділильного кола, перекочується по ньому без ковзання. Така пряма твірного контуру називається початковою. На рис. 1, а ділильна пряма 1 знаходиться на відстані хіт від ділильного кола, а значить, від початкової прямої 2. Ця відстань називається зміщенням вихідного твірного контуру, де хі = хіті/т коефіцієнт зміщення. Зміщення вважається додатним, якщо ділильна пряма і ділильне коло не перетинаються (рис. 9.17, а).
Зубчасті колеса, зуби яких утворені при х = 0, тобто коли початкова пряма твірного контуру є його ділильною прямою, називаються зубчастими колесами без зміщення (інколи — нульовими). При х ≠ 0 одержуємо зубчасті колеса із зміщенням.
Практично нарізання коліс із зміщенням ніяких ускладнень не викликає і досягається встановленням інструменту на відповідній відстані від осі заготовки. Можливість вибору зміщення при нарізанні зубчастих коліс дає змогу керувати у широких межах геометричними та якісними характеристиками передач.
На рис. 1, б зображено профілі зубів трьох коліс, що мають однакову кількість зубів, нарізані одним і тим самим інструментом, але з різним зміщенням: х1 < х2 < х3. Колеса мають однакові радіуси ділильного й основного кіл, а значить, профілі зубів усіх трьох коліс окреслені однією й тою самою евольвентою, але товщини зубів s1 = аЬ, s2 = ас, s3 = аf і радіуси кіл вершин ra1, ra2, ra3 у коліс будуть різними. Із збільшенням коефіцієнта зміщення x товщина зуба біля основи збільшується, а біля вершини зменшується, тобто коефіцієнт зміщення суттєво впливає на форму зуба. Отже, з трьох зубів, що розглядаються, зуб третього колеса буде найміцнішим. Крім цього, для евольвентної частини профілю зуба третього колеса використовується ділянка евольвенти, яка найвіддаленіша від її основного кола і має більший радіус кривизни, що сприяє зменшенню спрацювання і контактних напружень бічної поверхні зуба. Таким чином, вибираючи при проектуванні той чи інший коефіцієнт зміщення, можна впливати на форму зубів і на якість зубчастої передачі, наділяючи її необхідними властивостями. Проте слід зауважити, що така залежність форми зубів і властивостей передачі від коефіцієнта зміщення х суттєво відчутна при малих числах зубів і послаблюється в міру збільшення z.
Враховуючи, що початкова пряма інструменту обкочується без ковзання по ділильному колу заготовки, крок зубів твірного контуру слід відкласти z, разів на ділильному колі зубчастого колеса, яке нарізується.
Зміщення інструменту не змінює кроку по дузі ділильного кола, оскільки крок рейки по будь-якій прямій є сталим. Змінюється лише співвідношення між s і е (p=si+ei).
При нарізанні зубчастого колеса із зміщенням xim ділильна колова товщина його зуба
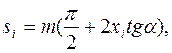 (1)
(1)
а ширина його западин
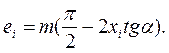 (2)
(2)
Розмір ділильної ніжки зубчастого колеса визначається глибиною проникнення зуба рейки у заготовку, згідно рис. 1,а
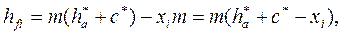 (3)
(3)
тоді радіус кола западин
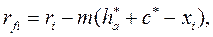 (4)
(4)
а радіус основного кола
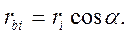 (5)
(5)
2. Розрахунок геометричних параметрів циліндричної прямозубої зубчастої передачі з умови щільного зачеплення двох коліс
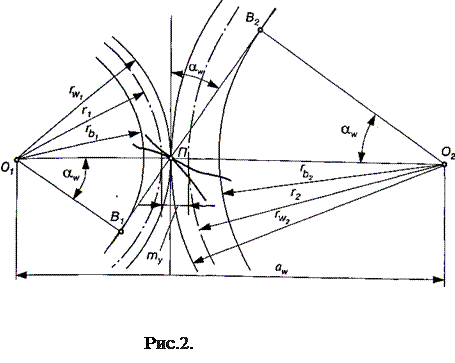
При щільному зачепленні зубчастих коліс (без бічного зазору між зубами), що нарізані зі зміщенням твірного контуру тхі центроїдами у відносному русі будуть початкові кола радіусів rw1, і rw. Радіуси цих кіл можна визначити з трикутників О1В1П і О2В2П (рис.2):
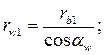
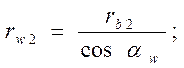 (6)
(6)
де  — кут зачеплення.
— кут зачеплення.
Кутом зачеплення називають кут між лінією зачеплення В1В2 і прямою,
перпендикулярною до лінії центрів. Цей кут чисельно дорівнює куту
профілю зубів кожного з коліс передачі у точці, що лежить на початковому колі.
Маючи на увазі, що 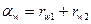 та враховуючи формули
та враховуючи формули
( 5 ), записуємо
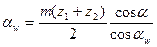 (7) ( 6)
(7) ( 6)
або 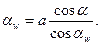 (8)
(8)
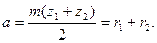 (9)
(9)
Тут a — ділильна міжосьова відстань, що дорівнює сумі радіусів ділильних кіл зубчастих коліс.
 |
Різниця міжосьової ан, і ділильної а відстаней називається сприймальним (видимим) зміщенням і позначається
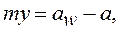 (10)
(10)
де у — коефіцієнт сприймального зміщення, що виражається залежністю
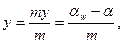 (11)
(11)
На рис. 2 сприймальне зміщення ту визначається найменшою відстанню між ділильними колами. Зокрема, якщо
х1 = х2 = 0 або х1=-х2, то 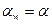 .
.
Виразами (9.35) або (9.36) можна скористатися лише після того, як буде знайдено кут зачеплення 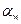 передачі, який можна визначити з умови, що початкові кола перекочуються один відносно одного без ковзання, а значить, товщина зуба по дузі початкового кола одного зубчастого колеса повинна дорівнювати ширині западини іншого по дузі його початкового кола,
передачі, який можна визначити з умови, що початкові кола перекочуються один відносно одного без ковзання, а значить, товщина зуба по дузі початкового кола одного зубчастого колеса повинна дорівнювати ширині западини іншого по дузі його початкового кола,
 |
тобто
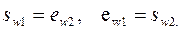 (12)
(12)
Попередньо знайдемо залежність для визначення товщини зуба і ширини западини на дузі довільного радіуса ry (рис.3), якщо зубчасте колесо нарізане зі зміщенням рейки хт. На основі побудованого рисунка можна записати
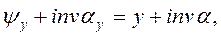 (13)
(13)
 де
де 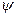 — половина кута товщини зуба на ділильному колі (ділильна кутова товщина);
— половина кута товщини зуба на ділильному колі (ділильна кутова товщина);  -- половина кутової товщини зуба на дузі кола радіуса ry
-- половина кутової товщини зуба на дузі кола радіуса ry
Замінюючи кутову товщину зуба коловою (s=2r 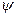 ), одержуємо
), одержуємо
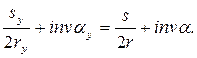 (14)
(14)
Після нескладних перетворень і з урахуванням залежностi (1), маємо формулу для визначення товщини зуба
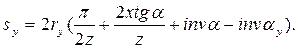 (15)
(15)
аналогічно отримуємо формулу для визначення ширини западини:
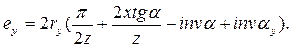 (16)
(16)
Використовуючи залежність (14) і (15), для початкового кола з урахуванням (11) та (5) маємо рівняння зачеплення циліндричної евольвентної передачі
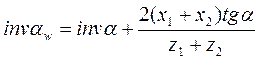 . (17)
. (17)
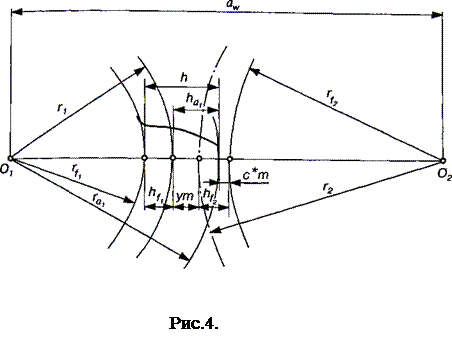 |
Діаметри кіл вершин, а значить, і висота ділильних головок розраховуються з умови одержання бажаного радіального зазору с у зачепленні зубчастих коліс. Стандарт не регламентує строго величину с. Найбільше розповсюдження одержали передачі, в яких радіальний зазор дорівнює с*т, де с*=0,25. Для таких передач визначимо величину ділильної головки На зуба (рис. 4).
Як видно з рис. 4, відстань між колами западин можна уявити як суму
 (18)
(18)
тут і далі індекси i, j можуть набувати значення: 1 або 2.
тоді повна висота зуба
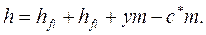 (19)
(19)
Висота ділильної головки зуба (за умови h1=h2=h)
 , (20)
, (20)
або з урахуванням залежності (3)
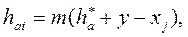 (21)
(21)
де xj -- коефіцієнт зміщення при нарізанні j-го зубчастого колеса; у- коефіцієнт сприймального зміщення. Отже, радіус кола вершин
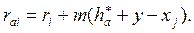 (22)
(22)
У ГОСТ 16532—70 розрахунок геометрії зубчастої передачі наведений з використанням коефіцієнта зрівняльного зміщення
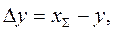 (23)
(23)
У такому випадку формула для визначення радіуса кола вершин має вигляд
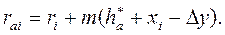 (24)
(24)
3. Особливості геометрії косозубих циліндричних передач
 |
Раніше розглядались здебільшого зачеплення прямозубими циліндричними колесами. У таких передачах контакт між зубами проходить по прямій, паралельній осям обертання, причому зуби одночасно по всій довжині входять у зачеплення й одночасно виходять із нього. Картина зачеплення у будь-якій площині, перпендикулярній до осі обертання коліс, однакова за геометрією і часом. Тому неточності, які завжди мають місце при виготовленні зубчастих коліс (наприклад, неточність профілю, несталість кроку та ін.), а також деформації та спрацювання деталей погіршують їх роботу (збільшується шум, зменшується довговічність передачі тощо). Крім цього, плавність роботи у прямозубих передач порівняно невелика.
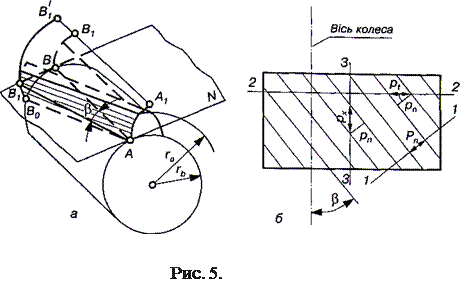
Для усунення вказаних недоліків, як уже зазначалось, на практиці часто використовують косозубі або шевронні циліндричні передачі (рис. 9.2, а, б). Бічну поверхню косого зуба утворює пряма АВ[ поверхні N (рис. 9.21, а), яка обкочується без ковзання відносно основного циліндра радіуса rb. Пряма АВ1 утворює з твірною АВ основного циліндра кут β. Цей кут називають кутом нахилу зубів. Кожна точка прямої АВ1 описує таку ж евольвенту, як і точка А, утворюючи при цьому не циліндричну, а гвинтову лінійчату евольвентну поверхню зуба.
Картина зачеплення зубів у косозубій передачі в будь-якому перетині, як і в прямозубій передачі, однакова. Проте на відміну від прямозубої передачі зачеплення у всіх перетинах відбувається несинхронно у часі, тобто зуби входять у зачеплення не зразу по всій довжині, а поступово.
Косозубі циліндричні зубчасті колеса нарізуються рейками, лінії зубів яких складають з віссю колеса, що нарізується, кут (3. На рис. 9.21, б зображено план косозубої вихідної твірної рейки, на якій нанесені лінії зубів. При такому розташуванні ліній зубів їх крок можна вимірювати у трьох плоских перетинах рейки:
а) перетин 1—1, нормальний до теоретичної лінії зубів, у
якому вимірюють нормальний крок рn;
б) перетин 2—2, перпендикулярний до осі зубчастого колеса,
що нарізається рейкою (торцевий перетин), у якому вимірюють
торцевий крок рt
в) перетин З— З (осьовий перетин) площиною, паралельною
осі зубчастого колеса, що нарізується рейкою, у якому вимірюють осьовий крок рx.
Контур зубчастої рейки в нормальному перетині і є тим вихідним твірним контуром, розміри якого залежать від розрахункового модуля m.
Тому 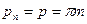 . (25)
. (25)
 Із рис. 5, б легко одержати значення торцевого і осьового кроків зубів залежно від нормального:
Із рис. 5, б легко одержати значення торцевого і осьового кроків зубів залежно від нормального:
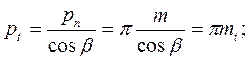
|
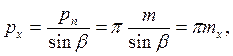
де mt i mx – відповідно торцевий і осьовий модулі, які визначаються формулами
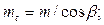 (26)
(26)
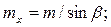 (27)
(27)
Для розрахунку геометричних параметрів косозубих зубчастих коліс важливо визначити параметри торцевого контуру косозубої рейки, оскільки цей контур профілює евольвенту зубчастого колеса.
На рис. 6 накладено профілі зуба косозубої рейки в торцевому (контурна лінія) і нормальному (штрихова лінія) перетинах. Товщина зуба і ширина западини рейки у її ділильній площині рівні між собою, причому в торцевому перетині
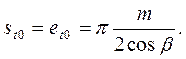 (28)
(28)
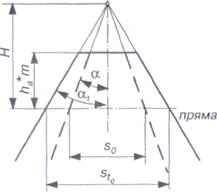
Кут профілю α, торцевого перетину рейки визначається з умови, що розмір Н від ділильної прямої до точки перетину бічних профілів зуба у будь-якому перетині один і той самий. Тоді можна записати
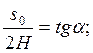 (29)
(29)
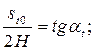 (30)
(30)
або
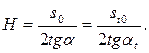 (31)
(31)
З урахуванням (28)
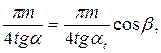 (32)
(32)
звідки 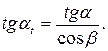 (33)
(33)
Коефіцієнт зміщення хt віднесений до торцевою модуля mt визначається з рівності зміщень у нормальному і торцевому перетинах:
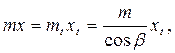 (34)
(34)
або
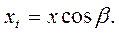 (35)
(35)
Доведення формул для розрахунку косозубих передач спеціально можна не виконувати, а використати формули для прямозубої передачі, переписавши останні з урахуванням того, що в торцевому перетині необхідно використовувати торцевий модуль mt, торцевий кут профілю αt і торцевий коефіцієнт зміщення . Виняток складають розмірів зубів за висотою для яких потрібно використовувати розрахунковий модуль m .
| <== предыдущая лекция | | | следующая лекция ==> |
| Евольвентная зубчата передача (продовження) | | | ОСНОВНІ ВИДИ МЕХАНІЗМІВ |
Дата добавления: 2016-06-15; просмотров: 6131;











