Евольвентная зубчата передача (продовження)

Коротке содержание:Классификация зубчатих передач. Поняття про блокуючий контур. Якісні показники для эвольвентной передачі.Коефіцієнт перекриття.Коефіцієнт форми зуба. Коефіцієнт питомого тиску. Коефіцієнт питомого ковзання.Оптимальний геометричний синтез зубчатої передачі.Програмне забезпечення САПР зубчатих передач. Косозубиє циліндрові эвольвентные передачі і особливості їх розрахунку.Коефіцієнт осьового перекриття.

Контрольні питання

Класифікація зубчатих передач

Циліндрові эвольвентные зубчаті передачі залежно від величини сприйманого зсуву класифікуються таким чином.

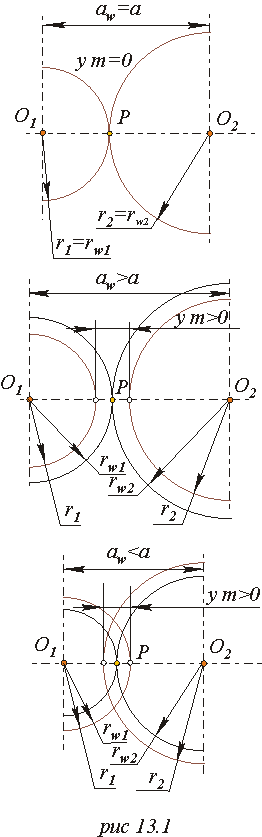
	нульові або равносмещенные (складені із зубчатих коліс без зсуву або з рівними, але протилежними по знаку зсувами) x1 = x2 = 0 або x1 = - x2, D1 = D2 = 0 або D1 = - D2 , yЧm = 0, у = 0, aw= а = r1 + r2, aw = а ;
позитивні (складені з коліс з позитивними зсувами або коли позитивний зсув одного колеса більше негативного зсуву іншого) x1 > 0, x2 > 0 або x1 > | - x2 |, D1 > 0, D2 > 0 або D1 > | - D2 |, yЧm > 0, у > 0, aw> а, aw > а ;
негативні (складені з коліс з негативними зсувами або коли негативний зсув одного колеса більше позитивного зсуву іншого) x1 <, x2 < 0 або x1 < - x2 |, D1 < 0, D2 < 0 або D1 < | - D2 |, yЧm < 0, у < 0, aw< а, aw < а .

Поняття про блокуючий контур зубчатої передачі

При проектуванні зубчатої передачі необхідно вирішити декілька завдань:

вибрати тип зубчатого механізму, його передавальне відношення і числа зубів коліс;

провести проектний прочностной розрахунок механізму і визначити величину міжосьової відстані або модуль зубчатих коліс( модуль зубчатих коліс округляється до найближчої величини із стандартного ряду модулів );

· провести геометричний розрахунок зубчатої передачі для вибраних коефіцієнтів зсуви початкового контура, які забезпечують виключення підрізування, зрізає і загострення зубів коліс і сприятливе або оптимальне поєднання якісних показників зубчатої передачі.

Для эвольвентных зубчатих передач, за пропозицією М.Б.Громана, область поєднань коефіцієнтів зсувів зубчатих коліс x1 і x2, що задовольняють обмеженням по тому, що зрізає у верстатному зачепленні, загостренню, заклинюванню в зачепленні евольвент і на перехідних кривих, по допустимих мінімальних або максимальних значеннях якісних показників, називають блокуючим контуром (рис.13.2). Межі блокуючого контура відсікають ті значення коефіцієнтів зсуву які недопустимі за вказаними умовами. Значення, розташовані усередині контура, допустимі, але кожній парі коефіцієнтів зсуву відповідає своє поєднання якісних показників. Для вибору коефіцієнтів зсуву на блокуючий контур наносяться изолинии якісних показників, з використанням яких усередині контура вибираються коефіцієнти зсуву з оптимальним поєднанням якісних показників. І.І.Болотовським і його співробітниками створені довідники, які містять блокуючі контури для великого числа зубчатих передач. Побудова блокуючого контура є трудомістким обчислювальним завданням і вимагає значних витрат навіть при застосуванні ЕОМ. В даний час, із зростанням продуктивності комп'ютерів, з'являється можливість геометричного синтезу оптимальних зубчатих передач без попередньої побудови блокуючого контура.

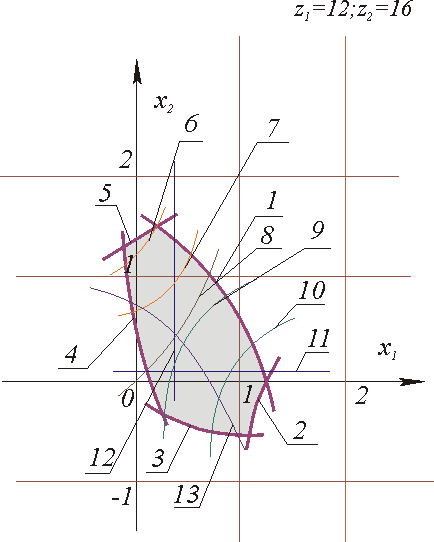Мал. 13.2

На мал. 13.2 обмежуючих ліній блокуючого контура: 1 - коефіцієнт торцевого перекриття ea =1; 2 - товщина зуба колеса z1 по колу вершин sa1 = 0; 3 - допустиме підрізування колеса z2 ; 4 - допустиме підрізування колеса z1 ; 5 - інтерференція або заклинювання з перехідною кривою колеса z2. Лінії якісних показників: 6 - лінія sa2 = 0.25m; 7 - лінія sa2 = 0.4m; 8 - лінія питомих ковзань l1=l2, що вирівнюються; 9 - лінія sa1 = 0.4m; 10 - лінія sa1 = 0.25m; 11 - лінія x2 = x2min ; 12 - лінія x1 = x1min ; 13 - лінія ea = 1.2.

Якісні показники циліндрової эвольвентной передачі.

До якісних показників циліндрової эвольвентной зубчатої передачі відносяться:

коефіцієнт торцевого перекриття

коефіцієнт корисної дії

коефіцієнт питомого ковзання

коефіцієнт питомого тиску

коефіцієнт форми зуба

Розглянемо ці коефіцієнти докладніше (виключивши з розгляду коефіцієнт корисної дії, як величину характеризує реальні, а не що розглядаються нами механізми, що ідеалізуються).

Коефіцієнт торцевого перекриття

Коефіцієнтом перекриття eg називається величина відношення кута перекриття зубчатого колеса до його кутового кроку, де під кутом перекриття розуміють кут на який повертається колесо за час зачеплення однієї пари зубів. Для циліндрових коліс розрізняють повні eg, торцеве ea і осьове перекриття:

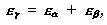
де осьове перекриття є тільки в косозубых передачах.

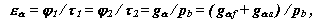
де

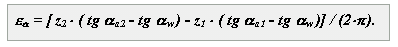
Коефіцієнт перекриття визначає величину зони двохпарного контакту, коли одночасно зачіпляються два послідовно розташованих зуба. Оскільки до закінчення зачеплення однієї пари зубів, наступна пара повинна увійти до контакту, не можна допускати в прямозубых передачах . Допустиме значення коефіцієнта перекриття винне декілька перевищувати одиницю і, залежно від призначення передачі і точності її виготовлення, вибирається в межах . Максимальне значення коефіцієнта перекриття для зубчатих коліс, оброблених інструментом із стандартним початковим контуром, що проводить, складає . Найбільш сприятливі величини коефіцієнта перекриття рівні цілим числам, наприклад двом або трьом. Забезпечити це можна тільки використовуючи інструмент з нестандартним початковим контуром, що проводить. Дробові значення коефіцієнта перекриття, наприклад близькі до півтора, приводять до циклічної зміни жорсткості передачі і до виникнення параметричних коливань.

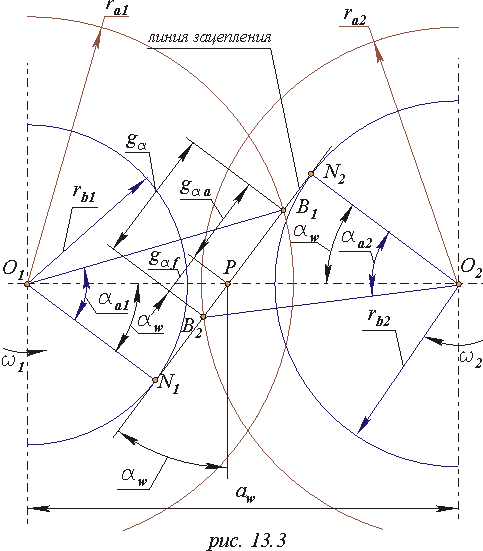
Коефіцієнт форми зуба

Геометрична форма зуба значною мірою визначає показники його як изгибной, так і контактній міцності. Оцінка впливу геометрії зуба на изгибную міцність здійснюється коефіцієнтом форми зуба Y. Цей коефіцієнт визначається через параметри балки параболиче-

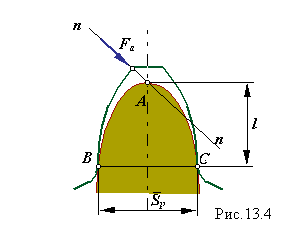
ского перетини (балки рівного опору вигину), яка вписується в контур зуба так, щоб вершина параболи розташовувалася в точці перетину осі зуба і нормалі до профілю у вершині, а гілки стосувалися профілю зуба у підстави ( див. схему на мал. 13.4). 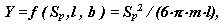де Sp - товщина зуба по хорді на колі, що проходить через точки дотику параболи і профілю зуба, l - висота від вершини параболи до хорди Sp .

Коефіцієнт питомого тиску.

Для характеристики впливу геометричної форми зуба на контактну міцність використовується коефіцієнт питомого тиску . З аналізу формули Герца, яка використовується для оцінки контактної напруги у вищій парі, можна укласти, що єдиний геометричний елемент в цій формулі - приведений радіус кривизни

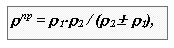
де - радіуси кривизни профілів в контактній крапці, знак + відноситься до зовнішнього зачеплення, - до внутрішнього. Щоб коефіцієнт тиску характеризував контактну напругу не-залежно від абсолютних розмірів зуба, які визначаються модулем, введено поняття питомого тиску як стосунки модуля до приведеного радіусу кривизни

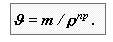
Для циліндрової прямозубой эвольвентной передачі:

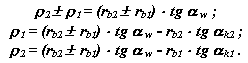
Тоді для зовнішнього зачеплення: при контакті в точці В2 (на виході зубів із зачеплення) :

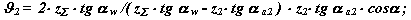
при контакті в точці В1 (на вході зубів в зачеплення)

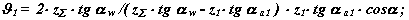
при контакті в полюсі точці Р:

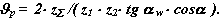
Коефіцієнт питомого ковзання.

Як показано вище, швидкість ковзання в точці контакту профілів вищої пари визначається наступним виразом :

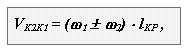
де l кр - відстань від точки контакту до полюса, знак "+" для зовнішнього зачеплення","- для внутрішнього. Величина зносу активних частин профілів у вищій парі в значній мірі залежить від їх відносного ковзання і від швидкості цього ковзання. Для оцінки ковзання при геометричних розрахунках зубчатих передач користуються коефіцієнтом питомого ковзання

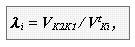
де Vtki - проекція швидкості контактної точки ланки i на контактну нормаль. З схеми эвольвентного зачеплення ( [ 1 ] стр.105 мал. 86 )

після підстановки і перетворень для колеса z1 при контакті в точці В2 (на виході зубів із зачеплення)

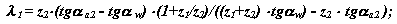
для колеса z2 при контакті в точці В1 (на вході зубів в зачеплення)

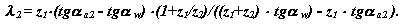
Графіки зміни коефіцієнтів питомого тиску і питомого ковзання по лінії зачеплення зубчатих коліс.

Оптимальний геометричний синтез зубчатої передачі.

Оптимальний геометричний синтез зубчатої передачі проводиться аналогічно оптимальному метричному синтезу механізмів важелів, але з використанням інших обмежень і інших якісних показників. Серед якісних показників необхідно розрізняти суперечливі і несуперечливі. Так із збільшенням зсувів питомий тиск і коефіцієнт форми зуба змінюються в бажаному напрямі, а коефіцієнт торцевого перекриття і товщини зубів по колах вершин зменшуються, що, при спрощеному розгляді, можна вважати за небажаний. Критерії або якісні показники, які при прийнятій зміні параметрів змінюються в бажаному напрямі вважаються за несуперечливих (оскільки не противоречат один одному), ті критерії, які при цьому змінюються небажаним чином, називаються суперечливими. За наявності суперечливих критеріїв ефективним методом пошуку оптимуму є метод "мінімізації поступок". При цьому методі спочатку проводиться оптимізація по кожному з даних критеріїв, визначаються значення критеріїв в оптимальних крапках і шукаються значення параметрів при яких відхилення кожного критерію від його оптимального значення будуть мінімальні. Необхідно відзначити, що можливості параметричної оптимізації достатньо скромні. Зазвичай в середньому можна отримати поліпшення по кожному з показників не більше 10 - 20%. Істотніших результатів можна досягти при переході до іншої схеми або іншого типу механізму. Крім того при геометричному синтезі зубчатій передачі складно орієнтуватися в поєднанні якісних показників. При аналізі ковзання необхідно враховувати, що створення стійкої масляної плівки в зоні контакту можливо при певних значеннях швидкості ковзання. У полюсі зачеплення швидкість ковзання дорівнює нулю і при проходженні полюса ця швидкість змінює свій знак. Тому в зубчатих передачах при дозаполюсном зачепленні в зоні близькою до полюса відбувається порушення масляної плівки, що приводить до підвищеного зносу в цій зоні за рахунок контактного вифарбовування - питтинга. З цих позицій переважними виявляються передачі з великими зсувами з до або заполюсным зачепленням, в яких швидкість ковзання направлена в один бік, не має нульових значень, тому умови для формування масляної плівки сприятливіші.

Програмне забезпечення САПР зубчатих передач.

У 70 - е роки були розроблені і прийняті ГОСТ на термінологію, прочностные і геометричні розрахунки эвольвентных зубчатих передач. Тому програмне забезпечення САПР зубчатих передач по всіх напрямах проводиться по розрахункових формулах і алгоритмах що рекомендується ГОСТ. У ГОСТ передбачено два види розрахунку геометрії:

по стандартному радіальному зазору в передачі;

по стандартній висоті зуба.

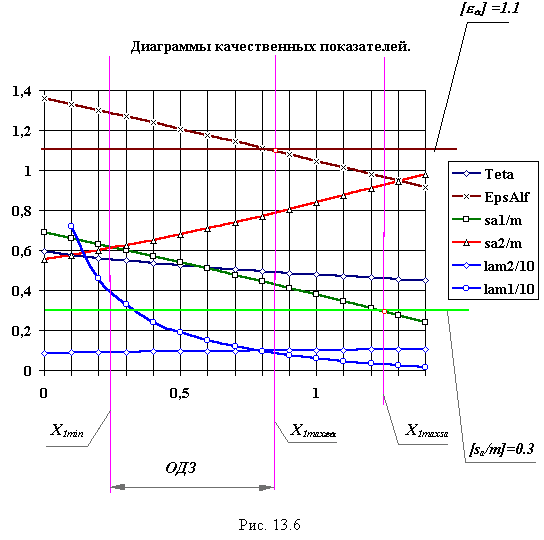
При вивченні курсу ТММ в МВТУ ім. Баумана прийнятий метод розрахунку по стандартній величині радіального зазору. Програмне забезпечення, що існує на кафедрі, розроблене для цього виду розрахунку і забезпечує розрахунок геометрії зовнішнього зачеплення при фіксованому значенні x2 = 0.5 і зміні x1 в діапазоні від 0 до 1.4 з шагом0.1. При виконанні курсового проекту по ТММ на підставі цього розрахунку будуються графіки якісних показників, визначається область допустимих рішень для коефіцієнта x1 і вибір цього по оптимальному поєднанню якісних показників. На мал. 13.6 приведений приклад графіка. При набутих допустимих значень

[Ea] =1.1. і [Sa/m]=0.3

обмеження на вибір коефіцієнта зсуву x1 :

по підрізуванню X1min = 0.24 ;

по загостренню колеса z1 : X1maxsa = 1.24;

по торцевому перекриттю :X1maxea = 0.84.

Таким чином, область допустимих значень (ОДЗ), в якій можна вибирати значення x1 0.24 > x1 > 0.84. цій області вибирається те значення x1, яке забезпечує якнайкраще поєднання якісних показників. Часто вибір коефіцієнта проводять по рекомендаціях ГОСТ. Для даного випадку силової зубчатої передачі з числами зубів z1 = 14 і z2 = 22

x1 = x2 = 0.5 .

Косозубиє циліндрові эвольвентные передачі і особливості їх розрахунку.

Косозубимі називаються циліндрові эвольвентные зубчаті передачі, бічна поверхня зуба якої утворена похилій прямій лежачою в плоскості, що проводить, і створюючою з лінією торкання з основним циліндром кут bb ( див. схему на мал. 13.7). При цьому евольвентами основного кола радіусу rb будуть криві лежачі в торцевій плоскості. Тому розрахунок геометрії циліндрової косозубой передачі проводиться по приведених вище формулах для торцевого перетину. Для передачі з косими зубами потрібно ввести декілька нових параметрів:

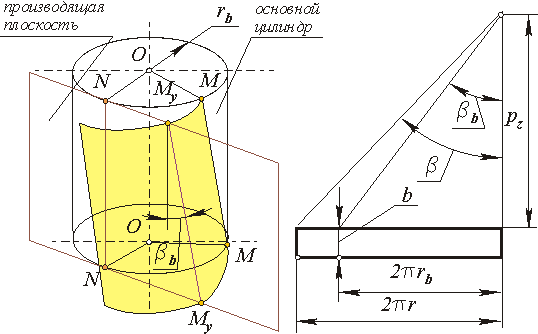
Мал. 13.7

осьовий крок - відстань між однойменними лініями сусідніх гвинтових зубів по лінії перетину плоскості осьового перетину зубчатого колеса з ділильною, початковою або іншою співісною поверхнею. На мал. 13.7 справа зображені розгортки ділильного і початкового циліндрів косозубого колеса. З цієї схеми:

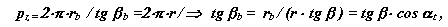
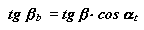
З схеми, зображеної на мал. 13.8

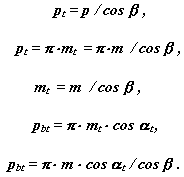
При нарізуванні косозубого колеса інструментальна рейка повертається на кут b, при цьому стандартний початковий контур, що проводить, розташовується в нормальній плоскості, а в розрахунковій торцевій плоскості утворюється інший, торцевий контур, параметри якого визначимо з схеми, приведеної на мал. 13.9.

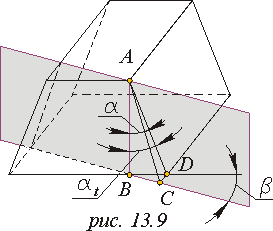
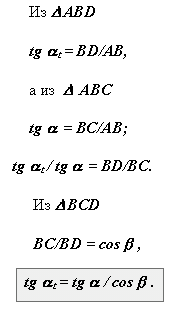
Для висотних співвідношень торцевого контура, що проводить:

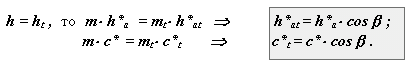
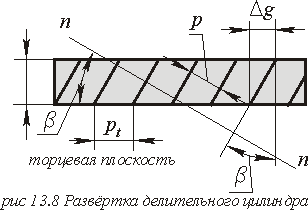
Коефіцієнт осьового перекриття.

У косозубых передачах величина коефіцієнта перекриття збільшується на величину торцевого перекриття, яке (мал. 13.8) рівне:

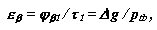
де

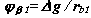- кут осьового перекриття для колеса z1 .

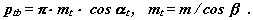
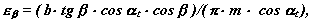
Контрольні питання до лекції 13

1. Для яких цілей використовуються зубчаті механізми? (стр.1)

2. Яка эвольвентная зубчата передача називається передачею без зсуву?(стр.1)

3. По яких ознаках класифікують зубчаті передачі?(стр.2)

4. Які основні завдання вирішуються при проектуванні эвольвентной передачі?(стр.2)

5. Перерахуєте основні якісні показники циліндрової эвольвентной передачі (стр.3)

6. Що показує коефіцієнт перекриття? (стр.3,4)

7. Що таке коефіцієнт торцевого перекриття? Виведіть формулу для ea.(стр.3)

8. Що називається косозубой эвольвентной зубчатою передачею?(стр.8)

9. Як записується формула для коефіцієнта eb осьового перекриття? (стр.10)