Уравнение состояния идеального газа

Установлено, что число независимых параметров, определяющих со-стояние равновесия системы, всегда равно числу тех способов, которыми система может обмениваться энергией с окружающей средой. Поскольку газ может обмениваться энергией двумя способами — в виде работы и те-плоты, то состояние газа должно полностью определиться значением двух параметров. Это позволяет решить уравнение состояния идеального газа относительно какого-либо параметра:

р = f (Т, V); T = f (р, V); V = f (р, Т).

Законы Бойля–Мариотта, Гей-Люссака и Шарля являются частными, устанавливающими связь между двумя параметрами состояния, если тре-тий параметр постоянен. Все эти три закона объединяются в один закон, который формулируется следующим образом: для данного газа произведе-ние давления на его объем пропорционально его абсолютной температуре. Математическая запись объединяемого закона выражается уравнением

где R — коэффициент пропорциональности, называемый газовой постоян-ной и зависящий только от рода газа; его размерность Дж/(кг·К).

Идеальные газы подчиняются закону Авагадро, утверждающему, что в равных объемах любого газа при одинаковой температуре и давлении со-держится одинаковое число молекул. Следствием этого закона является то, что произведение мольной массы на удельный объем для идеальных газов при постоянных Т и р есть постоянная величина

где V — объем киломоля газа; — мольная масса, моль.

При нормальных условиях (р_н = 0,1033 МПа; Т_н=273 К) один киломоль идеального газа занимает объем 22,4 м³. Для одного киломоля идеального газа уравнение состояния принимает следующий вид:

где R — универсальная газовая постоянная, равная 8314 Дж/(кмоль К).

Объем газа, находящегося при произвольных физических условиях, приводится к нормальным условиям по формуле:

В большинстве случаев рабочим телом в тепловых машинах являются не отдельные химически чистые газы, а их смесь (атмосферный воздух, продукты горения топлива, природные и искусственные газы).

Уравнение состояния газа справедливо также для газовых смесей, для которых оно принимает вид:

Давление смеси равно сумме парциальных давлений отдельных газов, составляющих данную смесь (закон Дальтона):

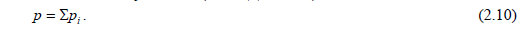
Парциальное давление отдельного газа в смеси, т. е. давление которое бы он создавал, если бы один занимал весь объем смеси, равно:

где r_i, g_i — соответственно объемные (мольные) и массовые доли отдельных газов в смеси.

Реальные газы хорошо подчиняются уравнению состояния идеального газа, когда их давление не очень большое, а температура не очень низкая.

Во всех других случаях наблюдаются отклонения от уравнения Клапейрона–Менделеева. Они вызваны тем, что молекулы реальных газов имеют конечные размеры (объем) и взаимодействуют друг с другом, при-чем тем сильнее, чем меньше расстояния между ними, т. е. чем больше плотность газа. В практике для термодинамических расчетов процессов с реальными газами используются табличные и графические зависимости параметров состояния, вычисленные на основе более точного учета осо-бенностей поведения этих веществ.

Теплоемкость

Теплоемкостью называется количество теплоты,необходимое для на-гревания вещества на один градус, отнесенное к единице массы, объема или числу молей. В соответствии с этим у газов различают теплоемкости: с_m —массовую,кДж/(кг К); с_v —объемную,кДж/(м³К); c —моль-ную, кДж/(кмоль К).

Взаимный пересчет этих теплоемкостей можно выполнить по формуле

Теплоемкость смеси газов равна сумме произведений массовой, объ-емной или мольной теплоемкостей компонентов на соответствующие их массовые или объемные доли.

Теплоемкость зависит от природы рабочего тела, его температуры, характера процесса, в котором происходит подвод или отвод теплоты.

Теплоемкость газов с повышением температуры увеличивается. Для технических расчетов пользуются значением средней теплоемкости в за-данном интервале температур.

Теплоемкость газов зависит также от давления. В термодинамике осо-бое значение имеет теплоемкость при постоянном давлении и теплоем-кость при постоянном объеме.

Эти теплоемкости взаимосвязаны уравнением Майера

Отношение с_р/с_v носит название показателя адиабаты. Теплоемкость твердых и жидких тел определяется физическими свой-

ствами вещества, не зависит от давления и слабо зависит от температуры; для практических расчетов она принимается за постоянную величину.