Точечные оценки параметров распределения
В §11 уже отмечалось, что оценками теоретических характеристик обычно служат соответствующие статистические характеристики. Чтобы эти оценки имели практическую ценность, они должны обладать некоторыми свойствами. В частности, оценки должны быть состоятельными.
Оценка 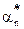 параметра α называется состоятельной, если при неограниченном увеличении числа испытаний она сходится по вероятности к оцениваемой величине, т.е.
параметра α называется состоятельной, если при неограниченном увеличении числа испытаний она сходится по вероятности к оцениваемой величине, т.е. 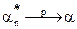 при n→ ∞. Как следует из замечания к теореме Чебышева (§22), среднее арифметическое измерений
при n→ ∞. Как следует из замечания к теореме Чебышева (§22), среднее арифметическое измерений 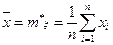 сходится по вероятности к математическому ожиданию mξ. Следовательно, эта оценка математического ожидания состоятельная. Если в качестве оценки математического ожидания взять величину
сходится по вероятности к математическому ожиданию mξ. Следовательно, эта оценка математического ожидания состоятельная. Если в качестве оценки математического ожидания взять величину 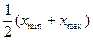 , то эта оценка, очевидно, не будет состоятельной.
, то эта оценка, очевидно, не будет состоятельной.
С помощью теоремы Чебышева можно доказать, что все статистические моменты, рассмотренные в §11, являются состоятельными оценками соответствующих теоретических моментов.
Второе требование, накладываемое на оценку, - это несмещенность. Оценка 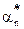 называется несмещенной, если ее математическое ожидание совпадает с оцениваемым параметром, т.е.
называется несмещенной, если ее математическое ожидание совпадает с оцениваемым параметром, т.е. 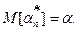 Это позволяет избежать систематической ошибки измерений.
Это позволяет избежать систематической ошибки измерений.
Докажем, что второй центральный статистический момент 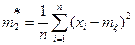 является несмещенной оценкой дисперсии
является несмещенной оценкой дисперсии 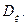 Действительно,
Действительно,
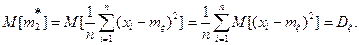
Итак, математическое ожидание от оценки равно оцениваемому параметру, следовательно, 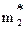 - несмещенная оценка.
- несмещенная оценка.
Если в качестве оценки дисперсии взять величину 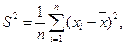 то эта оценка будет смещенной. Действительно, преобразуем
то эта оценка будет смещенной. Действительно, преобразуем 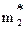 следующим образом:
следующим образом:
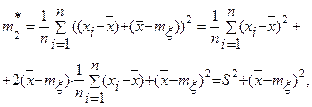
или 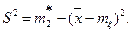 Найдем математическое ожидание
Найдем математическое ожидание 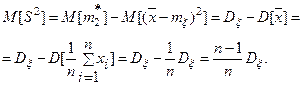
Воспользовались (5) §20, т.к. измерения xi независимые. Итак,
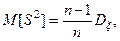 (1)
(1)
т.е. математическое ожидание оценки не равно оцениваемой величине, оценка S2 смещенная. Из (1) видно что
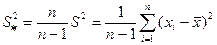 (2)
(2)
будет уже несмещенной оценкой дисперсии. В §11 именно эту величину мы взяли в качестве оценки дисперсии.
Оценка 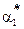 параметра
параметра 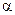 называется более эффективной, чем оценка
называется более эффективной, чем оценка 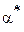 того же параметра, если
того же параметра, если 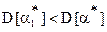 . Несмещенная оценка, дисперсия которой минимальная, называется эффективной. Заметим, что она не всегда существует.
. Несмещенная оценка, дисперсия которой минимальная, называется эффективной. Заметим, что она не всегда существует.
Иногда закон распределения известен, но неизвестны входящие в него параметры. Например, известно, что случайная величина подчиняется гамма-распределению (см. §12), а параметры λ и α неизвестны. Эти параметры можно оценить по выборке. Наиболее простым и распространенным методом получения оценок является метод моментов. Он состоит в приравнивании друг к другу теоретических и эмпирических моментов. Из полученных уравнений находят неизвестные параметры, которые и берут в качестве оценок. Оценки, полученные по методу моментов, являются состоятельными, но не являются, вообще говоря, эффективными и могут быть смещенными.
Пример 1. Оценить параметры λ и α гамма-распределения методом моментов.
Решение. Известно (см. пр. 6 §12), что 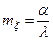 ,
, 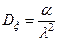 . Заменяя
. Заменяя 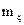 на
на 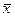 , а
, а 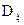 на
на 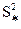 , получим систему:
, получим систему:
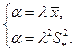
Решая ее, найдем 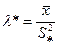 ,
, 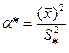 .
.
Эти оценки состоятельные, но смещенные.
Вторым наиболее распространенным методом нахождения оценок является метод наибольшего правдоподобия. Он дает состоятельную и эффективную (если она существует) оценку параметра, но она может оказаться смещенной.
Если (x1, x2,…, xn) - выборка случайной величины ξ, плотность распределения f(x,α) которой зависит от параметра α, то функцию
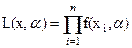 , x= (x1, x2,…, xn) (3)
, x= (x1, x2,…, xn) (3)
называют функцией правдоподобия. Можно доказать, что функция L(x,α) является плотностью распределения случайного вектора x=(x1, x2,…, xn), а поэтому максимуму функции L(x,α) соответствует наиболее правдоподобное значение ее аргумента α. Отсюда ясно, что за оценку параметра α берут то его значение α*, при котором функция L(x,α) достигает максимума. Необходимым условием максимума является равенство:
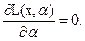 (4)
(4)
Разрешая уравнение (4) относительно α , получим оценку 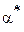 параметра α по методу функции правдоподобия. Следует, конечно, убедиться, что в точке
параметра α по методу функции правдоподобия. Следует, конечно, убедиться, что в точке 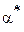 достигается максимум функции L(x,α).
достигается максимум функции L(x,α).
Если α =(α 1, α 2,…, α к), то вместо (4) получим
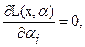 i=1,2,…,к. (4¢)
i=1,2,…,к. (4¢)
Пример 2. Оценить параметр λ в показательном законе распределения (см. пр.5 §12) методом функции правдоподобия.
Решение. Составим функцию правдоподобия 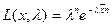 ,
, 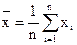 . Запишем уравнение правдоподобия (4):
. Запишем уравнение правдоподобия (4):
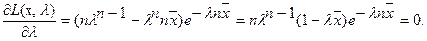
Решая последнее уравнение, найдем оценку параметра λ: 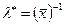 . Поскольку
. Поскольку 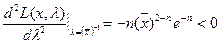 , то в точке
, то в точке 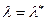 достигается максимум.
достигается максимум.
Дата добавления: 2020-02-05; просмотров: 630;











