Понятие о центральной предельной теореме

Центральная предельная теорема устанавливает условия, при которых предельный закон распределения суммы случайных величин 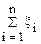при n→∞, является нормальным. Под центральной предельной теоремой понимают группу теорем, которые отличаются друг от друга условиями, накладываемыми на распределения случайных величин ξ_i. Мы рассмотрим простейший случай, когда случайные величины ξ_i попарно независимые и одинаково распределены.

Теорема. Если ξ₁, ξ₂,…, ξ_n независимые случайные величины, имеющие один и тот же закон распределения, то при неограниченном увеличении n закон распределения суммы

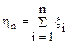(1)

стремится к нормальному.

Доказательство. Т.к. ξ_i одинаково распределены, то они имеют одни и те же числовые характеристики 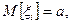D[ξ_i]=σ². Тогда 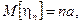D[η_n]=nσ². Нормируем случайную величину 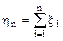. Получим

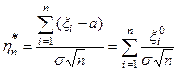, (2)

здесь 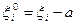– центрированная случайная величина. Очевидно, .

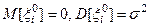Из §24 следует, что теорема будет доказана, если докажем, что характеристическая функция 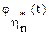нормированной величины (2) при n→∞ стремится к функции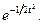

Пусть характеристическая функция центрированной величины 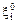равна φ(t), 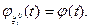Разложим ее в ряд Тейлора в окрестности t=0, сохранив три члена разложения. Согласно (7) §24 имеем:

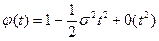. (3)

Используя свойства (1) и (2) §24, найдем характеристическую функцию случайной величины .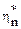

.

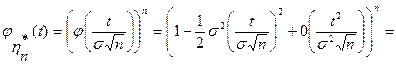
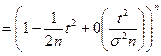Прологарифмируем последнее равенство

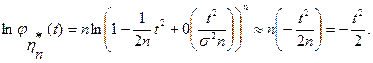
Последнее означает, что 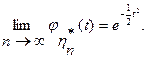Теорема доказана.

Пусть 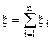- число появлений события А в n испытаниях Бернулли (см. §22). Параметрами случайной величины являются M[ξ]=np, D[ξ]=npq. Согласно доказанной теореме случайная величина ξ при больших n распределена приближенно по нормальному закону. Поэтому

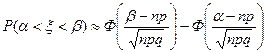. (4)

Здесь Ф(х) – интеграл вероятности. Формула (4) есть теорема Лапласа-Муавра.

При расчетах на ЭВМ неизбежны округления, что приводит к ошибкам результата вычислений (погрешность округления). Пусть 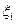– погрешность i-го округления. Будем считать ξ_i независимыми случайными величинами, равномерно распределенными на интервале (–e_, e). Пусть производится n сложений, тогда 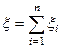– ошибка округления суммы. Если n достаточно велико, то согласно центральной предельной теореме суммарная ошибка ξ распределена по нормальному закону. Найдем его параметры. Очевидно, M[ξ_i]=0 в силу симметричности распределения, D[ξ_i]= 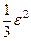(см. пр.4 §12). Тогда M[ξ]=0, 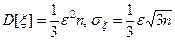. Если воспользоваться правилом "трех сигма" (см. п.7 §12), то можно считать, что ошибки округления не выйдут за границы интервала (-3σ_ξ, 3σ_ξ) или 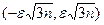. Это утверждение называют правилом Чеботарева.