Производная функции комплексного переменного.
Пример 1.
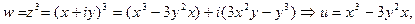
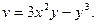 Эта функция однозначная.
Эта функция однозначная.
Пример 2.
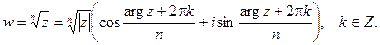
Эта функция многозначная (n-значная).
Пример 3. 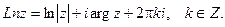
Эта функция бесконечнозначная.
Все эти функции заданы на всей комплексной плоскости, исключая бесконечно удаленную точку 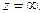 Последняя функция не определена еще и в точке
Последняя функция не определена еще и в точке 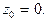 Заметим, что бесконечно удаленная точка
Заметим, что бесконечно удаленная точка 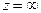 на комплексной плоскости единственная.
на комплексной плоскости единственная.
Говорят, что функция 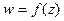 отображает множество E в множество G.
отображает множество E в множество G.
|
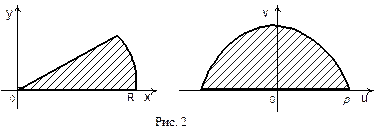
Пусть E - круговой сектор: r<R, 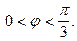 Найдем область G, в которую отобразит функция
Найдем область G, в которую отобразит функция 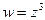 область E. Пусть
область E. Пусть 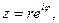 тогда
тогда 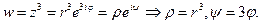 Отсюда ясно, что функция
Отсюда ясно, что функция 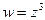 отображает сектор E в верхний полукруг радиуса
отображает сектор E в верхний полукруг радиуса 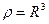 (см. рис. 2).
(см. рис. 2).
Это отображение взаимнооднозначное, т.е. каждой точке множества Е (прообразу) соответствует единственная точка (образ) множества G. И наоборот, образу соответствует единственный прообраз.
Заметим, что границе области E соответствует граница области G.
Возьмем теперь в качестве области E сектор 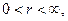
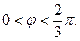 При отображении
При отображении 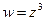 точки, лежащие на луче
точки, лежащие на луче 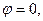 отображаются в точки луча
отображаются в точки луча 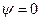 и точки, лежащие на луче
и точки, лежащие на луче 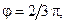 отображаются в точки того же луча
отображаются в точки того же луча 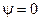
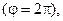 т.е. взаимная однозначность отображения нарушается.
т.е. взаимная однозначность отображения нарушается.
Чтобы сохранить взаимную однозначность отображения, сделаем разрез комплексной плоскости 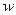 по положительной полуоси u и будем считать, что верхний берег разреза – это образ луча
по положительной полуоси u и будем считать, что верхний берег разреза – это образ луча 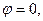 а нижний – образ луча
а нижний – образ луча 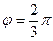 (см. рис. 3).
(см. рис. 3).
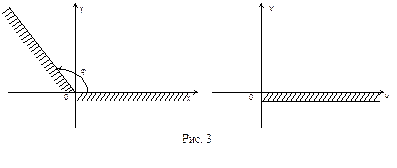
Если областью E является сектор 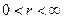
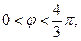 то взаимная однозначность отображения
то взаимная однозначность отображения 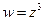 опять нарушится. Чтобы ее сохранить, предположим, что при изменении аргумента прообраза от
опять нарушится. Чтобы ее сохранить, предположим, что при изменении аргумента прообраза от 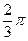 до
до 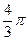 образ соскальзывает с нижнего разреза плоскости
образ соскальзывает с нижнего разреза плоскости 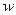 на второй (нижний) слой той же плоскости
на второй (нижний) слой той же плоскости 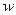 (см. рис. 4).
(см. рис. 4).
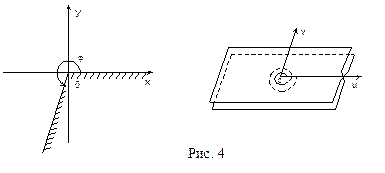
В этом случае образы точек, лежащие на лучах, например, 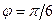 и
и 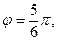 будут лежать на одном луче
будут лежать на одном луче 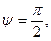 но первые на верхнем листе плоскости
но первые на верхнем листе плоскости 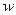 , а вторые на нижнем, и взаимная однозначность отображения сохранится.
, а вторые на нижнем, и взаимная однозначность отображения сохранится.
Ясно ,что вся плоскость z функцией 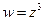 отобразится в трехслойную плоскость
отобразится в трехслойную плоскость 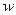 с разрезом по положительной полуоси u. При этом верхний берег разреза первого листа совпадает с нижним берегом разреза третьего.
с разрезом по положительной полуоси u. При этом верхний берег разреза первого листа совпадает с нижним берегом разреза третьего.
Если 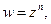
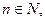 то образом плоскости z будет n–слойная (n-листная) плоскость
то образом плоскости z будет n–слойная (n-листная) плоскость 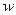 с разрезом по действительной полуоси u. Такой многослойный образ называют поверхностью Римана.
с разрезом по действительной полуоси u. Такой многослойный образ называют поверхностью Римана.
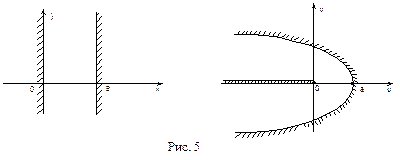
Пусть областью определения функции 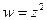 является полоса
является полоса 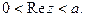 Найдем образ линии
Найдем образ линии 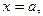 т.е. кривую, в которую она отображается функцией
т.е. кривую, в которую она отображается функцией 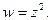
Запишем уравнение прямой 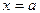 в комплексном виде:
в комплексном виде: 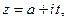
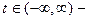 параметр.
параметр.
Тогда
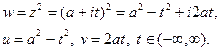 (1)
(1)
Уравнения (1) являются параметрическими уравнениями образа линии 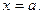 Исключив параметр t, получим
Исключив параметр t, получим 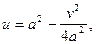 т.е. образом линии
т.е. образом линии 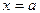 является парабола.
является парабола.
При 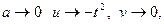 т.е. прямая
т.е. прямая 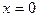 отобразится в отрицательную полуось. Полоса
отобразится в отрицательную полуось. Полоса 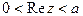 отобразится, очевидно, в часть плоскости внутри параболы с разрезом по отрицательной полуоси (см. рис. 5).
отобразится, очевидно, в часть плоскости внутри параболы с разрезом по отрицательной полуоси (см. рис. 5).
Рассмотрим последовательность комплексных чисел
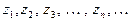 (2)
(2)
Определение 2.Число 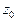 называется пределом последовательности (2), если
называется пределом последовательности (2), если 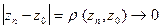 при
при 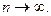 Пишут
Пишут 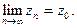
Если 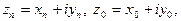 то из определения 2 следует
то из определения 2 следует
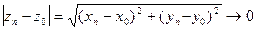 при
при 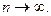 Следовательно,
Следовательно,
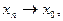
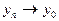 при
при 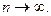 (3)
(3)
Очевидно и обратное утверждение, если выполняется (3), то 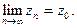
Если 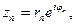
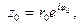
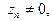
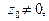 то
то 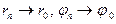 при
при 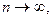 если
если 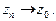 (4)
(4)
Определение 3.Число 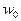 называется пределом однозначной функции
называется пределом однозначной функции 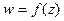 в точке
в точке 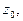 если для всякой последовательности аргумента
если для всякой последовательности аргумента 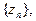 сходящейся к
сходящейся к 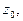 соответствующая последовательность значений функции
соответствующая последовательность значений функции 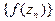 сходится к
сходится к 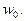 Пишут
Пишут 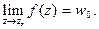
Подчеркнем, что если предел функции существует, то он не зависит ни от способа, ни от пути стремления последовательности 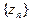 к точке
к точке 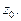
Если 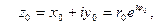
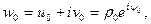
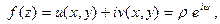
то из существования предела 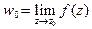 следует существование следующих пределов:
следует существование следующих пределов: 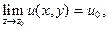
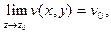 (5)
(5)
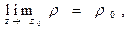
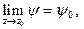
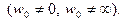 (6)
(6)
Если 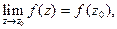 то функция называется непрерывной в точке
то функция называется непрерывной в точке 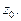 Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Например, функция
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Например, функция 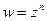 непрерывна во всей комплексной плоскости.
непрерывна во всей комплексной плоскости.

Производная функции комплексного переменного.
Дата добавления: 2020-02-05; просмотров: 657;











