Лекция 17 ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
17.1 ЭЛЕКТРОМАГНЕТИЗМ
17.1.1 Явление электромагнитной индукции
17.1.2 Явление самоиндукции
17.1.3 Явление взаимной индукции
17.1.4 Энергия магнитного поля
17.1.5 Система уравнений Максвелла
Некоторые примеры
Контрольные вопросы
17.1 ЭЛЕКТРОМАГНЕТИЗМ
17.1.1 Явление электромагнитной индукции
Если взять замкнутый проводящий контур (например, круговой виток провода), то при поднесении к нему постоянного магнита в витке возникнет электрический ток; аналогичный эффект возникает и при удалении магнита от витка, ток при этом идёт в противоположном направлении. То, что электрическое поле способно породить магнитное (при прохождении по проводнику постоянного электрического тока) было открыто Эрстедом в 1820 году, для установления обратного эффекта, то есть того, что магнитное поле способно порождать электрическое, понадобилось еще десять лет. Существенным здесь оказалось то, что для проявления эффекта магнитное поле должно меняться со временем.
Открытое в 1831 году Фарадеем явление электромагнитной индукции заключается в возникновении э. д. с. при изменении магнитного потока через поверхность, ограниченную замкнутым контуром или заметаемую проводником в процессе движения.
Направление протекания тока в замкнутом контуре определяется по правилу Ленца: индукционный ток всегда направлен так, чтобы препятствовать причине, его вызывающей.
Пример 1
Пусть к замкнутому проволочному контуру северным полюсом приближается постоянный магнит (см. рис. 17.1). Как будет направлен ток, индуцируемый при этом в контуре?
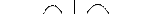 Прежде всего, объясним, почему ток вообще возникнет. Приближение магнита к контуру (стрелка 1) означает, что магнитное поле, в котором находится виток, становится всё более и более сильным (его индукция возрастает), увеличивается и магнитный поток Fчерез площадь, ограниченную контуром. Увеличение магнитного потока (то есть, его изменение) приводит к возникновению э. д. с. индукции в контуре, и по нему начинает идти ток.
Прежде всего, объясним, почему ток вообще возникнет. Приближение магнита к контуру (стрелка 1) означает, что магнитное поле, в котором находится виток, становится всё более и более сильным (его индукция возрастает), увеличивается и магнитный поток Fчерез площадь, ограниченную контуром. Увеличение магнитного потока (то есть, его изменение) приводит к возникновению э. д. с. индукции в контуре, и по нему начинает идти ток.
Для ответа на вопрос о направлении тока сначала следует нарисовать линии индукции поля магнита (на рисунке они направлены вниз). Теперь применим правило Ленца: «индукционный ток должен препятствовать причине, его вызывающей». Для того, чтобы воспрепятствовать возрастанию потока, образованного полем, линии индукции которого направлены вниз, необходимо создать в контуре ток, магнитное поле которого характеризуется линиями индукции, направленными вверх –  . Если вспомнить картину силовых линий, создаваемых кольцом с током (рис. 13.2.в) и применить правило винта, легко понять, что возникающий ток должен иметь направление, указанное на рисунке стрелкой I1.
. Если вспомнить картину силовых линий, создаваемых кольцом с током (рис. 13.2.в) и применить правило винта, легко понять, что возникающий ток должен иметь направление, указанное на рисунке стрелкой I1.
Если магнит удаляется от контура (стрелка 2), магнитный поток уменьшается. Препятствовать этому уменьшению можно, лишь создав индукционный ток, линии индукции которого будут теперь направлены вниз –  : ток пойдёт в направлении стрелки I2.
: ток пойдёт в направлении стрелки I2.
Пример 2
Пусть прямой, параллельный оси Z проводник, имеющий длину l, движется поступательно со скоростью u вдоль оси X в плоскости XZ, находясь в однородном магнитном поле c индукцией B, силовые линии которого направлены вдоль оси Y (рис. 17.2).
 При движении проводника в магнитном поле на находящиеся в нём заряды действует сила Лоренца. В металле перемещаться могут лишь электроны, и под действием этой силы они начинают смещаться к дальнему от нас концу проводника, в результате чего он заряжается отрицательно (а ближний конец – положительно). Накопление зарядов происходит до тех пор, пока сила
При движении проводника в магнитном поле на находящиеся в нём заряды действует сила Лоренца. В металле перемещаться могут лишь электроны, и под действием этой силы они начинают смещаться к дальнему от нас концу проводника, в результате чего он заряжается отрицательно (а ближний конец – положительно). Накопление зарядов происходит до тех пор, пока сила  , действующая на электрон со стороны возникшего электрического поля, не уравновесит силу Лоренца
, действующая на электрон со стороны возникшего электрического поля, не уравновесит силу Лоренца 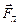 , при этом между концами проводника создаётся разность потенциалов j1 - j2. Так как FЛ = euB (здесь e – заряд электрона, а u – скорость его движения вместе с проводником, причём угол между векторами
, при этом между концами проводника создаётся разность потенциалов j1 - j2. Так как FЛ = euB (здесь e – заряд электрона, а u – скорость его движения вместе с проводником, причём угол между векторами  и
и  равен 90°), а FЭ = eE, где E – напряжённость возникшего электрического поля, то, с учётом того, что связь между напряжённостью E и разностью потенциалов на концах проводника выражается формулой E = (j1 - j2)/l, можно записать: euB = e(j1 - j2)/l, или
равен 90°), а FЭ = eE, где E – напряжённость возникшего электрического поля, то, с учётом того, что связь между напряжённостью E и разностью потенциалов на концах проводника выражается формулой E = (j1 - j2)/l, можно записать: euB = e(j1 - j2)/l, или
j1 - j2 = luB. (17.1)
В нашем случае сила Лоренца играет роль сторонней, разделяющей заряды в движущемся проводнике. Запишем закон Ома для участка неоднородной цепи: I(R + r) = j1 - j2 + E. Поскольку в состоянии равновесия ток по проводнику не идёт (I = 0), следовательно,
E =-(j1 - j2) = - luB = - l  B = -
B = -  B = -
B = - 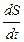 B,
B,
где dS – площадь, заметаемая проводником в процессе движения.
Если учесть, что dS×B = dFМ, где dFМ – магнитный поток через поверхность dS, то окончательная формула будет выглядеть так:
E =- 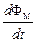 . (17.2)
. (17.2)
Данная формула оказывается справедливой не только при поступательном, но и при вращательном движении проводника, причём вектор скорости не обязательно должен быть перпендикулярен силовым линиям. Аналогичное выражение описывает возникновение э. д. с. и в замкнутом контуре при изменении магнитного потока через мысленно натянутую на него поверхность. При этом контур может быть неподвижен, а меняется магнитное поле.
Таким образом, э. д. с. индукции равна взятой с обратным знаком скорости изменения магнитного потока через поверхность, ограниченную замкнутым контуром или заметаемую проводником в процессе движения (закон Фарадея). Знак «минус» в формуле (17.2) отражает уже упоминавшееся выше правило Ленца: индукционный ток направлен так, чтобы препятствовать причине, его вызывающей.
Если контур содержит не один, а N витков, то в формулу (17.2) вместо магнитного потока FМ через один виток следует подставлять выражение Y = NFМ; параметр Y называется потокосцеплением и также измеряется в веберах.
Явление электромагнитной индукции лежит в основе работы генераторов электрического тока. В таких устройствах для получения электрической энергии проволочную рамку (точнее – систему рамок), находящуюся в магнитном поле, приводят во вращение с помощью потоков воды или пара, двигателей внутреннего сгорания или просто усилиями собственных мускулов.
В заключение заметим, что индукционные токи, которые возникают при изменении магнитного потока, могут течь не только в проволочных контурах, но и в объёме массивных проводников, заметно нагревая их. Эти токи называются токами Фуко; данное явление используется, например, для плавки металлов.
17.1.2 Явление самоиндукции
Электрический ток I, идущий в проводящем контуре, создаёт собственное магнитное поле и соответствующий этому полю собственный магнитный поток ФМ, который сам пронизывает поверхность, ограниченную контуром. При изменении I меняется и ФМ (очевидно, ФМ ~ I), вследствие чего в контуре возникает добавочная э. д. с. Явление возникновения э. д. с. в контуре при изменении силы тока в нём называется самоиндукцией.
Прямую пропорциональную зависимость ФМ от I (или же, если контур содержит несколько витков, – потокосцепления Y от I) можно выразить формулой ФМ =LI, в которой коэффициент
L =  , (17.3)
, (17.3)
зависящий от свойств материала (М) среды, в которой находится контур, от его размера (Р) и формы (Ф), называется индуктивностью. В СИ индуктивность измеряется в генри (в честь физика, открывшего явления самоиндукции), 1 Гн = 1 Вб×А-1.
Учитывая связь ФМ с I, для возникающей э. д. с. можно записать:
E =- 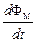 =-
=- 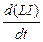 =-
=-  . (17.4)
. (17.4)
Если индуктивность контура является константой (не меняются со временем ни размер, ни форма контура, остаются теми же свойства окружающей среды), то тогда  = 0, и
= 0, и
E =-L 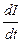 . (17.5)
. (17.5)
Зачастую эту формулу называют законом Генри для явления самоиндукции; как и раньше знак «минус» отражает необходимость выполнения для индукционного тока правила Ленца.
Пример
Продемонстрируем, как выводится формула для индуктивности тороида (или бесконечно длинного тонкого соленоида) и рассмотрим, от чего она зависит.
Ранее мы вывели формулу, согласно которой индукция магнитного поля внутри тороида, содержащего n витков на единицу длины,
B = m0nI = 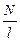 m0I,
m0I,
где l – длина тороида, N – число витков в нём, I – сила тока, идущего по тороиду. Применяя закон полного тока, можно получить аналогичную формулу для магнитного поля, создаваемого внутри тороида, не «пустого» внутри, а навитого на сердечник, изготовленный из материала с магнитной проницаемостью m:
B = mm0nI = 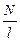 mm0I,
mm0I,
Используя данное соотношение, можно записать выражение для магнитного потока через один виток (площадь, ограниченную витком обозначим S): Ф = BS = 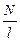 mm0IS и для общего магнитного потока (потокосцепления) через все N витков:
mm0IS и для общего магнитного потока (потокосцепления) через все N витков:
Y = 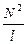 mm0IS.
mm0IS.
Таким образом, согласно определению (L =  ), получаем:
), получаем:
L = 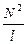 mm0S = mm0n2lS. (17.6)
mm0S = mm0n2lS. (17.6)
Сделаем некоторые выводы.
– L действительно зависит от свойств среды (от магнитной проницаемости m) сердечника, от размеров проводящего контура (то есть от числа витков N и его длины l), а также – от его формы (мы воспользовались формулой для индукции B внутри тонкого тороида, а не какого-либо иного объекта).
– Для того, чтобы индуктивность оставалась постоянной требуется не только неизменность N и l, формы тороида, но независимость от времени m. Последнее может не выполняться, например, при использовании ферромагнитных сердечников: изменение силы тока в контуре ведёт к изменению напряженности магнитного поля H в сердечнике, но m = m(H) – см. прошлую лекцию, следовательно, магнитная проницаемость тоже будет меняться.
– Формула 17.6 позволяет продемонстрировать, в каких единицах измеряется магнитная постоянная:
[m0] = [L] 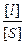 = Гн×
= Гн×  = Гн×м-1.
= Гн×м-1.
17.1.3 Явление взаимной индукции
Если два проводящих контура расположить неподалёку друг от друга (или надеть на общий ферромагнитный сердечник), то окажется, что при изменении силы тока в одном из контуров, во втором возникнет э. д. с.
Явление возникновения э. д. с. в одном контуре при изменении силы тока в другом называется явлением взаимной индукции.
 Сказанное поясняется рисунком 17.3, на котором изображены два контура (А и Б), расположенных в воздухе неподалёку друг от друга. При увеличении силы тока I1в контуре А в контуре Б возникает э. д. с. взаимной индукции, причём ток I2 будет иметь такое направление, чтобы уменьшить магнитной поток, создаваемый током I1 (см. правило Ленца). Направление протекания тока I2 и силовые линии создаваемого им магнитного поля рис. 17.3 показаны пунктиром.
Сказанное поясняется рисунком 17.3, на котором изображены два контура (А и Б), расположенных в воздухе неподалёку друг от друга. При увеличении силы тока I1в контуре А в контуре Б возникает э. д. с. взаимной индукции, причём ток I2 будет иметь такое направление, чтобы уменьшить магнитной поток, создаваемый током I1 (см. правило Ленца). Направление протекания тока I2 и силовые линии создаваемого им магнитного поля рис. 17.3 показаны пунктиром.
Аналогичная картина будет наблюдаться и в случае, если сила тока I1 будет оставаться неизменной, но контур А мы начнём приближать к контуру Б.
Если Ф1Б – магнитный поток, создаваемый током I1 через поверхность, ограниченную контуром Б, то э. д. с. EБ, возникающая в этом контуре, может быть рассчитана по формуле
EБ = - LБ1  . (17.7)
. (17.7)
Множитель LБ1, входящий в эту формулу, носит название коэффициента взаимной индукции; его величина зависит от магнитных свойств материала среды, в которой находятся контуры А и Б, от их размеров, формы.
Ситуацию можно «обратить»: менять ток I2 в контуре Б и наблюдать возникновение э. д. с. EА в контуре А:
EА = - LА2  . (17.8)
. (17.8)
В формуле (17.8) Ф2А – магнитный поток, создаваемый током I2 через поверхность, ограниченную контуром А, а LА2 – коэффициент взаимной индукции (в СИ измеряется в генри).
В воздухе LА2 = LБ1, даже если контуры А и Б разные (например, два соленоида, имеющие неодинаковое число витков N1 и N2) однако, если их надеть на общий ферромагнитный (или ферритовый) сердечник, то тогда может оказаться, что LА2 ¹ LБ1. Возникающее отличие обусловлено зависимостью магнитной проницаемости среды m от напряжённости магнитного поля H, которая, в свою очередь, определяется числом витков в том соленоиде, который создаёт магнитное поле (напомним: внутри длинного тонкого соленоида и тороида B = mm0nI, или H = nI).
Явление взаимной индукции используется в работе трансформаторов: устройств, в которых на общий замкнутый сердечник, изготовленный из ферромагнитного материала, надеты две проволочные катушки-обмотки, содержащие разное (N1 и N2) число витков. Если первую катушку (первичную обмотку) подключить к источнику переменной э. д. с. E1, то в ней возникнет переменный ток I1, который создаст меняющееся со временем магнитное поле, локализованное внутри сердечника. Переменный магнитный поток, в свою очередь, индуцирует э. д. с. во вторичной обмотке, надетой на этот же сердечник, и если вторичная обмотка разомкнута (такой режим называется режимом холостого хода)
 =
= 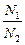 . (17.9)
. (17.9)
Если число витков во вторичной обмотке N2, больше числа витков в первичной обмотке N1, трансформатор называется повышающим (E2 > E1), если N2 < N1, – понижающим (E2 < E1).
17.1.4 Энергия магнитного поля
 Представим себе, что в цепи, изображённой на рис. 17.4, идёт электрический ток. Если ключ К перевести из положения 1 в положение 2, источник э. д. с. окажется отсоединённым, но зато образуется замкнутая цепь, состоящая их катушки с индуктивностью L и резистора с сопротивлением R. Ток, проходивший по катушке, начнёт спадать до нуля, но при этом в ней возникнет э. д. с. самоиндукции, и спад не будет мгновенным. За время спада э. д. с. самоиндукции успеет совершить работу, в ходе выполнения которой магнитная энергия перейдёт во внутреннюю (тепловую) энергию резистора. В соответствии с определением электродвижущей силы, работа сторонних сил dAСТ по перенесению малого заряда dq рассчитывается, как dAСТ = Edq. Полная работа, которую успеют совершить сторонние силы (вызванные явлением самоиндукции) за время спада тока от I до нуля, равна:
Представим себе, что в цепи, изображённой на рис. 17.4, идёт электрический ток. Если ключ К перевести из положения 1 в положение 2, источник э. д. с. окажется отсоединённым, но зато образуется замкнутая цепь, состоящая их катушки с индуктивностью L и резистора с сопротивлением R. Ток, проходивший по катушке, начнёт спадать до нуля, но при этом в ней возникнет э. д. с. самоиндукции, и спад не будет мгновенным. За время спада э. д. с. самоиндукции успеет совершить работу, в ходе выполнения которой магнитная энергия перейдёт во внутреннюю (тепловую) энергию резистора. В соответствии с определением электродвижущей силы, работа сторонних сил dAСТ по перенесению малого заряда dq рассчитывается, как dAСТ = Edq. Полная работа, которую успеют совершить сторонние силы (вызванные явлением самоиндукции) за время спада тока от I до нуля, равна:
AСТ =  = -L
= -L  = -L
= -L  =
=  .
.
Как известно, работа является мерой изменения энергии. Это означает, что совершившая работу катушка индуктивности в момент отключения источника питания обладала энергией WМ, связанной с магнитным полем, изменение которого и порождает э. д. с. самоиндукции. WМ = AСТ, или энергия магнитного поля
WМ =  . (17.10)
. (17.10)
Если катушка индуктивности представляет собой тороид или длинный тонкий соленоид, для которых, согласно формуле (17.6), L = mm0n2lS = mm0n2V, где V – объём пространства внутри тороида (там, где сосредоточено магнитное поле), можно записать:
WМ =  =
= 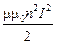 V =
V =  V =
V = 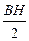 V.
V.
Здесь учтено, что внутри тороида B = mm0nI, а H = B/mm0 = nI. Таким образом, мы можем записать выражение для объёмной плотности энергии магнитного поля:
wЭЛ =  =
= 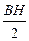 . (17.11)
. (17.11)
Данная формула справедлива не только для магнитного поля внутри тороида, но и вообще для любого магнитного поля.
В заключение заметим: если мы увеличиваем ток в катушке от нуля до некоторого значения I (напряжённость магнитного поля при этом растёт до некоторого значения H), мы совершаем работу против сторонних сил, вызванных явлением самоиндукции,
A = - AСТ =  =
= 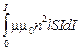 = V
= V 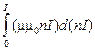 = V
= V 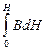 .
.
Таким образом, на графике зависимости B(H) совершаемая нами работа, приходящаяся на единицу объёма, численно равна площади под соответствующей кривой. В частности, если внутри катушки индуктивности находится ферромагнитный сердечник, график зависимости B(H) имеет вид петли гистерезиса, и работа, совершаемая за цикл по перемагничиванию единицы объёма сердечника, оказывается численно равной площади петли:
 =
=  . (17.12)
. (17.12)
Чем больше площадь петли гистерезиса, тем значительнее потери энергии, требуемые для перемагничивания сердечника.
17.1.5 Система уравнений Максвелла
Вершиной развития классической электродинамики явилось построение теории электромагнетизма, в основе которой лежит система уравнений Максвелла.
Пусть в замкнутом контуре длиной l, содержащем N1 источников э. д. с. Ei, идёт постоянный электрический ток. Сторонние силы совершают работу по разделению заряда q, но такую же затем совершают силы электрического поля внутри источников, обеспечивающие протекание тока в самом контуре. По определению работа первых AСТ = q 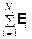 , работа вторых A =
, работа вторых A =  =
= 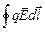 , и
, и
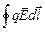 = q
= q 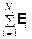 , или
, или  =
= 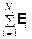 .
.
Сумма э. д. с. здесь алгебраическая: для тех источников, которые «помогают» протеканию тока в цепи, Ei нужно брать со знаком «плюс», для тех, которые «мешают» – со знаком «минус». Открытое Фарадеем явление электромагнитной индукции говорит о том, что источником э. д. с. может явиться переменное магнитное поле, и это также следует учесть при подсчёте указанной суммы:
 = -
= - 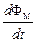 +
+ 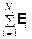 . (17.13)
. (17.13)
Максвелл предположил, что данное уравнение справедливо не только для замкнутого проводящего контура, по которому идёт электрический ток, но и для любого замкнутого контура, мысленно выбранного в пространстве. С учётом этого замечания формула (17.11) стала первым уравнением системы.
В основе второго уравнения лежит закон полного тока (теорема о циркуляции вектора напряжённости магнитного поля), согласно которой  , где
, где  – алгебраическая сумма токов (N2 – их число), которые пронизывают поверхность, мысленно натянутую на контур. Максвелл обратил внимание на то, что изменение электрического поля в некоторой области пространства может быть интерпретировано, как изменение заряда в этой области. Действительно, теорема Гаусса для электрического поля утверждает, что для системы, состоящей из N3 зарядов qi,
– алгебраическая сумма токов (N2 – их число), которые пронизывают поверхность, мысленно натянутую на контур. Максвелл обратил внимание на то, что изменение электрического поля в некоторой области пространства может быть интерпретировано, как изменение заряда в этой области. Действительно, теорема Гаусса для электрического поля утверждает, что для системы, состоящей из N3 зарядов qi,  , и, следовательно,
, и, следовательно, 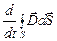 =
=  =
=  . Поток вектора электрического смещения (интеграл вида
. Поток вектора электрического смещения (интеграл вида  ) часто обозначается просто ФЭ, а ток
) часто обозначается просто ФЭ, а ток  называется током смещения(IСМ). Согласно Максвеллу, уравнение закона полного тока должно быть записано в виде
называется током смещения(IСМ). Согласно Максвеллу, уравнение закона полного тока должно быть записано в виде  = IСМ +
= IСМ +  , или
, или
 =
= 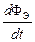 +
+  . (17.14)
. (17.14)
Это – второе уравнение Максвелла, оно также справедливо для любого мысленно выбранного в пространстве замкнутого контура.
Третье и четвёртое уравнения системы – это формулы теорем Гаусса для электрического и магнитного полей. Максвелл предположил, что они справедливы не только для постоянных, но и для переменных полей.
Кроме перечисленных четырёх уравнений в систему входят ещё три уравнения-связки, позволяющие выражать  через
через 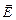 ,
,  через
через  , и
, и 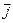 (плотность тока) через
(плотность тока) через 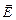 с помощью удельной электропроводности s.
с помощью удельной электропроводности s.
В итоге система уравнений Максвелла может быть представлена в виде[14] (17.15).




 ,
,
 = e0e
= e0e 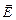 (17.15)
(17.15)
 =
= 
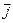 = s
= s 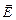 .
.
Данная система говорит о взаимосвязи электрического и магнитного полей, которая проявляется в том, что любое изменение магнитного поля обязательно приводит к появлению электрического поля (явление электромагнитной индукции), а изменение электрического поля, в свою очередь, сопровождается возникновением магнитного поля.
Теория Максвелла и предложенная им система уравнений позволяют решить основную задачу электродинамики: по заданному распределению в пространстве токов и зарядов вычислить значения напряжённости электрического и магнитного полей в нужной точке в требуемый момент времени. Теория Максвелла – основной инструмент для расчёта параметров антенн приёмников и передатчиков электромагнитного излучения, систем связи (радио-, спутниковой, сотовой и т. д.), устройств, усиливающих, ослабляющих и отражающих электромагнитные волны, описания взаимодействия электромагнитных волн с веществом и многих других процессов. После создания этой теории даже некоторое время считалось, что Максвеллом даны ответы практически на все вопросы электродинамики, и дальнейшая работа физиков сведётся лишь к уточнению некоторых аспектов теории и решению конкретных практических задач. Позднее оказалось, однако, что это не так (в частности, электромагнитное излучение обладает квантовыми свойствами, о которых речь пойдёт в следующей части курса). Кроме того, сама классическая теория не свободна от недостатков:
– Теория макроскопична (имеет дело с временами и расстояниями, много большими размеров атомов и соответствующими атомарным процессам временами).
– Теория феноменологична (даёт ответы на вопрос «как пользоваться уравнениями», но не дает ответа на вопрос «почему уравнения именно таковы»).
Тем не менее, как уже говорилось, теория Максвелла имеет громадное практическое значение, и с некоторыми аспектами этой теории мы ещё ознакомимся в следующем семестре.
Некоторые примеры
- Независимо от англичанина М.Фарадея (и даже несколько раньше него) явление электромагнитной индукции открыл американский физик Д.Генри. Но он не спешил с публикацией результатов своих исследований, и когда попытался сделать это, обнаружил, что он уже не первый. «Мне следовало печатать всё это раньше… И откуда мне было знать, что кто-то другой по ту сторону Атлантического океана занимается той же проблемой?» – с горечью писал он своему другу-издателю. Но, несмотря на неудачу, Генри не прекращает работать, открывает явление самоиндукции и успевает опубликовать сообщение об открытии на пару недель раньше, чем это попытался сделать Фарадей, также открывший это явление.
- Вращение системы проводящих рамок в магнитном поле с целью получения э. д. с. индукции – основной способ выработки электрического энергии. Коэффициент полезного действия процесса зависит от конструкции устройства, заставляющего рамки вращаться. Так, к. п. д. лучших тепловых электростанций не превышает 40 %, у серийных реакторов атомных станций этот параметр меньше (до 32 – 35 %), в то время как к. п. д. крупных гидроэлектростанций может приближаться к отметке 90 %!
- Явление взаимной индукции, которое используется в трансформаторах для преобразования переменного напряжения, позволяет делать это с очень высокой эффективностью: к. п. д. серийных трансформаторов обычно превышает 98 %.
- Из уравнений Максвелла следует, что меняющееся магнитное поле, силовые линии которого, как известно, всегда замкнуты, порождает меняющееся со временем электрическое поле, силовые линии которого также оказываются замкнутыми! Такое поле называют вихревым.
[1] Заметим – любую кривую можно представить в виде совокупности участков окружностей разных радиусов, набора парабол и т. д.
[2] Аббревиатура МРФ помогает запомнить, что именно Материалом, Размерами и Формой определяется величина многих физических параметров различных объектов: их электроёмкости, электрического сопротивления, индуктивности и т. д.
[3] На самом деле движение оказывается более сложным: ось испытывает нутации, то есть одновременно с движением по конусу имеет место добавочное колебательное движение оси вращения гироскопа в направлении, перпендикулярном конусообразной поверхности.
[4] Напомним, что в математике изменение функции вида W2 - W1 называется приращением и обозначается символом DW; разница вида W1 - W2 называется убылью; очевидно, что убыль равна -DW.
[5] В 1915 году Эйнштейн заложил основы теории тяготения, получившей название общей теории относительности (ОТО). В основе ОТО лежит постулат об эквивалентности массы, как характеристики инертных свойств тела (см. второй закон Ньютона), и массы, как параметра, характеризующего гравитационное притяжение двух тел (см. закон Всемирного тяготения).
[6] Более строгие рассуждения приводят к выводу, что одновременно происходит поворот объекта относительно вертикальной оси.
[7]Формула (7.5) крайне полезна для проведения приближённых вычислений. Пусть, например, возникла задача посчитать, сколько получится, если 1,01 возвести в степень 100. Никакой калькулятор тут не поможет: возникнет переполнение разрядов, но мы можем записать: (1,01)100 = (1 + 0,01)100 » 1 + 100×0,01 = 2.
Существуют и другие полезные формулы для приближённых вычислений: так, следует помнить, что при малых значениях аргумента, таких, что x £ 0,1 (рад), sinx » tgx » x, и что при ׀x׀ << 1 можно записать: ex » 1 + x.
[8] Напомним, что единицу измерения какой-либо физической величины обозначают символом этой величины, помещённым в квадратные скобки.
[9] Вообще говоря, при определённом соотношении между R1, R2, R4 и R5 (например, при R1 = R2 = R4 = R5) возможна ситуация, когда ток через резистор R3 не идёт, и тогда резисторы R1 и R2 (а также R4 и R5) можно считать включёнными последовательно.
[10] Ранее мы уже отмечали, что в электростатическом поле циркуляция вектора его напряжённости равна нулю, то есть  = 0.
= 0.
[11]И вновь формула не является альтернативой тексту теоремы, поскольку из формулы не следует, что замкнутая поверхность может иметь любую форму (в том числе – такую, которая нам удобна для проведения вычислений).
[12]Существуют и другие типы магнетиков: антиферромагнетики, ферриты, антиферримагнетики и др.
[13]Сравните способ введения намагниченности  с тем, как ранее был введён вектор поляризованности
с тем, как ранее был введён вектор поляризованности  .
.
[14]Это – так называемый «интегральный» вид системы (используются интегралы «поток» и «циркуляция» вектора). В ряде случаев систему уравнений Максвелла удобно записывать в «дифференциальном» виде (для бесконечно малых объёмов и площадей) с использованием математических операций «дивергенции» и «ротора» вектора (см., например, Савельев И.В. Курс общей физики, Т. 2).
Дата добавления: 2020-02-05; просмотров: 777;











