Лекция 15 МАГНИТНОЕ ПОЛЕ. ЧАСТЬ III
15.1 ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ (Часть III)
15.1.1 Работа по перемещению проводника с током в магнитном поле
15.1.2 Магнитный момент витка с током. Виток с током в однородном и неоднородном магнитных полях
15.2 МАГНИТОЕ ПОЛЕ В ВЕЩЕСТВЕ
15.2.1 Гипотеза Ампера. Гиромагнитное отношение
15.2.2 Намагниченность  . Теорема о циркуляции вектора магнитной индукции в веществе. Вектор напряжённости магнитного поля
. Теорема о циркуляции вектора магнитной индукции в веществе. Вектор напряжённости магнитного поля  . Закон полного тока
. Закон полного тока
15.2.3 Связь векторов  ,
,  и
и  . Виды магнетиков. Парамагнетизм
. Виды магнетиков. Парамагнетизм
Некоторые примеры
Вопросы для повторения
15 ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ (Часть III)
15.1.1 Работа по перемещению проводника с током
в магнитном поле
Сила Ампера, действующая в магнитном поле с индукцией  на проводник длиной l, по которому идёт ток I, может привести его в движение и совершить при этом работу:
на проводник длиной l, по которому идёт ток I, может привести его в движение и совершить при этом работу:
dA = ( 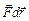 ) = Fdr×cosj = Fdr =
) = Fdr×cosj = Fdr = 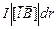 = IlB×sina×dr,
= IlB×sina×dr,
где a – угол между вектором  (его направление совпадает с направлением движения положительных зарядов в проводнике) и вектором магнитной индукции
(его направление совпадает с направлением движения положительных зарядов в проводнике) и вектором магнитной индукции  (рис. 15.1). Поскольку проводник движется под действием силы Ампера
(рис. 15.1). Поскольку проводник движется под действием силы Ампера 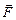 , угол j между вектором перемещения
, угол j между вектором перемещения 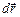 и самой силой везде равен нулю; это означает, что косинус угла между этими векторами, входящий в виде сомножителя в скалярное произведение
и самой силой везде равен нулю; это означает, что косинус угла между этими векторами, входящий в виде сомножителя в скалярное произведение 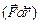 , равен единице.
, равен единице.
 С учётом того, что площадь, «заметаемая» проводником в процессе движения, вычисляется, как dS = l×dr, и того, что sina = cosb, выражение для расчёта работы силы Ампера можно переписать в виде
С учётом того, что площадь, «заметаемая» проводником в процессе движения, вычисляется, как dS = l×dr, и того, что sina = cosb, выражение для расчёта работы силы Ампера можно переписать в виде
dA = IlB×sina×dr = IBdScosb.
Но, согласно определению магнитного потока, FМ = 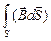 , или dFМ =
, или dFМ = 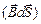 , следовательно, dA = I dFМ. Таким образом, работу по перемещению проводника с током в магнитном поле можно рассчитать, используя формулу
, следовательно, dA = I dFМ. Таким образом, работу по перемещению проводника с током в магнитном поле можно рассчитать, используя формулу
A = I×DFМ. (15.1)
Здесь DFМ – магнитный поток через поверхность, заметаемую проводником с постоянным током I в процессе движения.
Данная формула справедлива и в случаях, когда проводник движется не поступательно, а разворачивается в магнитном поле, при деформации, а также при переносе в область с другим значением магнитной индукции любого замкнутого контура с током I.
В заключение отметим: формула (15.1) позволяет легко выразить единицу измерения магнитного потока (вебер) через основные единицы СИ: 1 Вб = 1 Дж×А-1 = 1 кг×м2×с-2×А-1.
15.1.2 Магнитный момент витка с током.
Виток с током в однородном и неоднородном магнитных полях
Сила, действующая на прямой проводник с током в однородном магнитном поле, заставляет двигаться его поступательно. Картина меняется, если проводник имеет форму замкнутого витка, например, – прямоугольной рамки. Рассмотрим, что происходит в этом случае.
Пусть прямоугольная проводящая рамка, по которой идёт ток, расположена в однородном магнитном поле так, что нормаль к её поверхности составляет некоторый угол a с силовыми линиями. На каждый из участков рамки действует своя сила, причём направления этих сил – разные (сказанное поясняется рисунками 15.2.а), на котором изображена рамка с током в магнитном поле, и 
15.2.б), где представлен вид сверху этой же рамки).
Используя правило левой руки, можно определить направления этих сил и убедиться в том, что при данной ориентации рамки в пространстве они стремятся: а) развернуть рамку так, чтобы угол a стал равен нулю, и б) в итоге растянуть рамку.
Пусть теперь поле, в котором находится рамка, неоднородно. Увеличение индукции магнитного поля графически отображается, в виде сгущения силовых линий (на рис. 15.3.а) и 15.3.б) такое сгущение соответствует правой части рисунка). Силы, действующие на разные участки рамки, теперь не только направлены в разные стороны, но и не одинаковы по величине. Нетрудно заметить, однако, что и в этом случае они стремятся развернуть рамку так, чтобы нормаль к её поверхности (выбираемая по правилу винта в соответствии с током в рамке) оказалась направлена вдоль силовой линии.
Развернувшаяся рамка не останется на месте: действующие на неё силы (на рис. 15.3.б) это силы 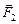 и
и 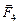 ) имеют не только компоненты
) имеют не только компоненты  и
и 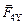 , стремящиеся растянуть рамку, но и компо
, стремящиеся растянуть рамку, но и компо 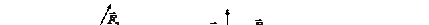
ненты  и
и 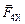 , которые втягивают рамку с током в область сильного магнитного поля.
, которые втягивают рамку с током в область сильного магнитного поля.
Для описания поведения витка произвольной формы удобно использовать следующее определение.
Магнитным моментом витка с током I будем называть выражение вида
 = I
= I 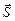 = IS
= IS 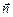 . (15.2)
. (15.2)
Здесь 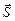 – псевдовектор, характеризующий поверхность, мысленно натянутую на виток:
– псевдовектор, характеризующий поверхность, мысленно натянутую на виток: 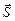 = S
= S 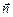 , где S – площадь этой поверхности, а
, где S – площадь этой поверхности, а 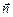 – единичный вектор нормали к данной поверхности, причём его направление по правилу винта согласовано с направлением протекания тока по витку.
– единичный вектор нормали к данной поверхности, причём его направление по правилу винта согласовано с направлением протекания тока по витку.
Нетрудно заметить: при помещении витка с током в магнитное поле он стремится развернуться так, чтобы его магнитный момент был ориентирован вдоль силовой линии, втягиваясь в область сильного поля. Ситуация подобна той, которую мы описывали в случае электрического поля, так же вёл себя диполь с электрическим дипольным моментом  : этот вектор тоже стремился выстроиться по направлению силовых линий, а сам диполь – втянуться в область с большей напряженностью поля.
: этот вектор тоже стремился выстроиться по направлению силовых линий, а сам диполь – втянуться в область с большей напряженностью поля.
Ещё одно замечание: направление вектора  совпадает с направлением вектора магнитной индукции поля, создаваемого на оси витка самим током, идущим по этому витку.
совпадает с направлением вектора магнитной индукции поля, создаваемого на оси витка самим током, идущим по этому витку.
В однородном поле (рис. 15.2) развернуть рамку стремятся силы 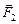 и
и 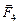 , моменты которых направлены в одну сторону (вверх), поэтому для суммарного момента
, моменты которых направлены в одну сторону (вверх), поэтому для суммарного момента 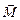 этих сил можно записать:
этих сил можно записать:
÷ 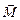 ê = F2
ê = F2 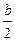 sina + F4
sina + F4 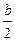 sina = B×I×l×
sina = B×I×l× 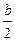 sina + B×I×l×
sina + B×I×l× 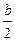 sina = B×I×(bl) sina =
sina = B×I×(bl) sina =
= B×I×S×sina = B×pm×sina = ½[ 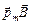 ]½.
]½.
Очевидно, что момент пары сил 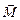 максимален (M = Mmax), когда угол a между векторами
максимален (M = Mmax), когда угол a между векторами  и
и  равен 90º. В этом случае
равен 90º. В этом случае
B =  =
=  .
.
Это соотношение может быть использовано для определения величины вектора индукции магнитного поля.
Явление поворота витка в магнитном поле лежит в основе работы электродвигателей постоянного и переменного тока. Дело в том, что если после окончания поворота витка изменить направление силы тока в нём (например, переключением скользящих вместе с витком контактов), то вращение продолжится, поскольку в момент переключения вектор  станет антипараллелен вектору
станет антипараллелен вектору  . После очередного поворота и переключения контакта направление протекания тока вновь поменяется, и т. д. В реальных моторах одновременно поворачивается не один, а десятки или даже сотни витков, намотанных на общий сердечник; каждый из них снабжён скользящими контактами, обеспечивающими изменение направления протекания тока в нужный момент времени.
. После очередного поворота и переключения контакта направление протекания тока вновь поменяется, и т. д. В реальных моторах одновременно поворачивается не один, а десятки или даже сотни витков, намотанных на общий сердечник; каждый из них снабжён скользящими контактами, обеспечивающими изменение направления протекания тока в нужный момент времени.
15.2 МАГНИТОЕ ПОЛЕ В ВЕЩЕСТВЕ
15.2.1 Гипотеза Ампера. Гиромагнитное отношение
По характеру воздействия магнитного поля на различные материалы все их можно разделить на несколько групп, среди которых большую часть составляют парамагнетики, диамагнетики и ферромагнетики[12]. Парамагнетики и диамагнетики очень слабо взаимодействуют с магнитным полем, причём парамагнетики втягиваются в область сильного поля, а диамагнетики, наоборот, выталкиваются из него. На ферромагнетики магнитное поле оказывает сильное влияние, изготовленные из таких материалов объекты притягиваются магнитами и сами могут становиться таковыми.
 |
Для объяснения природы магнитных свойств вещества Ампер выдвинул гипотезу, согласно которой любой материал можно представить в виде совокупности невидимых глазу из-за своих малых размеров кольцевых микротоков. В ненамагниченном состоянии все микротоки (и их магнитные моменты) ориентированы хаотически, а поскольку
 совпадает по направлению с вектором индукции магнитного поля, создаваемого самим витком на его оси, магнитное поле внутри образца отсутствует вовсе (рис. 15.4.а). При внесении образца в магнитное поле микротоки начинают поворачиваться (рис. 15.4.б), и хотя тепловое движение и взаимодействие токов друг с другом мешают развороту, тем не менее, с увеличением индукции внешнего магнитного поля упорядоченная ориентация микротоков становится всё более явно выраженной (рис. 15.4.в). Общее магнитное поле в веществе является теперь суперпозицией внешнего поля
совпадает по направлению с вектором индукции магнитного поля, создаваемого самим витком на его оси, магнитное поле внутри образца отсутствует вовсе (рис. 15.4.а). При внесении образца в магнитное поле микротоки начинают поворачиваться (рис. 15.4.б), и хотя тепловое движение и взаимодействие токов друг с другом мешают развороту, тем не менее, с увеличением индукции внешнего магнитного поля упорядоченная ориентация микротоков становится всё более явно выраженной (рис. 15.4.в). Общее магнитное поле в веществе является теперь суперпозицией внешнего поля  и суммарного поля
и суммарного поля  всех микротоков, что и накладывает свой отпечаток на поведение в магнитном поле всего образца в целом.
всех микротоков, что и накладывает свой отпечаток на поведение в магнитном поле всего образца в целом.
Используя данную гипотезу, можно объяснить явление парамагнетизма, однако сама она не может дать ответ основной на вопрос: что это такое – микротоки, какова их физическая природа? Во времена Ампера о строении вещества люди имели ещё весьма смутное представление, но сейчас даже школьник знаком с полуклассической теорией Бора строения атома, и способен предположить, что микротоки можно считать результатом движения по орбитам вокруг ядра электронов, которые входят в состав атома. Каждый электрон, движущийся по своей орбите – это микроток, и если таких электронов не один (как у водорода) а больше, то, сложив векторно магнитные моменты, соответствующие их орбитальному движению, получаем некоторый усреднённый магнитный момент атома в целом.
 Воспользовавшись этим представлением, покажем, как должен быть связан магнитный момент электрона, движущегося вокруг ядра по круговой орбите, с его моментом импульса – параметром, характеризующим вращательное движение электрона (см. рис. 15.5).
Воспользовавшись этим представлением, покажем, как должен быть связан магнитный момент электрона, движущегося вокруг ядра по круговой орбите, с его моментом импульса – параметром, характеризующим вращательное движение электрона (см. рис. 15.5).
Напомним: моментом импульса L материальной точки (а электрон можно считать такой точкой) относительно некоторой оси (в нашем случае – оси вращения) называется выражение вида  = [
= [  ], причём
], причём
L = rp = rmu,
где r – расстояние до оси (у нас – радиус орбиты), p – импульс точки (p = mu, где m – масса электрона, u – его линейная скорость). Направление вектора  согласовано с вектором скорости
согласовано с вектором скорости 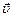 по правилу винта (на рисунке 15.5 вектор
по правилу винта (на рисунке 15.5 вектор  направлен вверх).
направлен вверх).
В свою очередь, интерпретируя движение электрона, как протекание электрического тока (его направление противоположно направлению вращения электрона, частицы, имеющей отрицательный заряд), можно рассчитать магнитный момент получающегося «витка» – круговой орбиты, по которой движется заряд e, совершая один оборот за время T (соответствующий ток I =  ):
):
pm = IS =  pr2.
pr2.
Так как направление вектора  согласовано с направлением протекания тока по правилу винта, то на рисунке этот вектор направлен вниз.
согласовано с направлением протекания тока по правилу винта, то на рисунке этот вектор направлен вниз.
Учтём теперь, что u = 2pr/T. Тогда  = -
= -  pr2×
pr2× 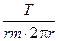 , или
, или
 = -
= -  . (15.3)
. (15.3)
Формула (15.3) носит название орбитального гиромагнитного отношения; знак «минус» в ней говорит о том, что вектор момента импульса и вектор магнитного момента электрона при орбитальном движении направлены в противоположные стороны (то есть проекции этих векторов на любую выделенную осьдолжны иметь разные знаки).
В справедливости соотношения для парамагнитных и диамагнитных материалов можно убедиться на практике; об одном из экспериментов (опыте Штерна - Герлаха) будет рассказано позднее в разделе «Квантовая механика». В случае ферромагнетиков данное отношение (обозначим его pms/Ls) не связано с орбитальным движением, и к тому же оно оказывается в два раза больше:
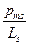 = -
= -  . (15.4)
. (15.4)
15.2.2 Намагниченность  . Теорема о циркуляции вектора
. Теорема о циркуляции вектора
магнитной индукции в веществе. Вектор напряжённости
магнитного поля  . Закон полного тока
. Закон полного тока
Принимая гипотезу Ампера, при расчёте индукции магнитного поля в любой среде помимо внешнего поля следует теперь учитывать и поля, создаваемые микротоками, которые соответствуют движению электронов в атомах. Для этого вводится усреднённая характеристика вещества – намагниченность  ; величина этого вектора равна отношению суммарного магнитного момента некоторого объёма DV вещества к величине этого объёма (единица измерения
; величина этого вектора равна отношению суммарного магнитного момента некоторого объёма DV вещества к величине этого объёма (единица измерения  в СИ – А×м-2)[13].
в СИ – А×м-2)[13].
 =
=  . (15.5)
. (15.5)
В этой формуле N – общее число микротоков в объёме DV. Таким образом, можно сказать, что намагниченность  имеет смысл магнитного момента единицы объёма вещества.
имеет смысл магнитного момента единицы объёма вещества.
Если все  направлены в одну сторону,
направлены в одну сторону,
 = n
= n  , (15.6)
, (15.6)
где n – число микротоков (атомов) в единице объёма (то есть, их концентрация).
Рассмотрим, как учитывается наличие микротоков при применении теоремы о циркуляции вектора  . Данная проблема актуальна, поскольку, теперь нам будет нужно складывать не только «макротоки» IiМАКРО, которые пронизывают натянутую на контур поверхность (в виде отдельных проводников с током или пучков заряженных частиц), но и большое число микротоков IiМИКРО (электронных орбит атомов), пронизывающих эту же поверхность:
. Данная проблема актуальна, поскольку, теперь нам будет нужно складывать не только «макротоки» IiМАКРО, которые пронизывают натянутую на контур поверхность (в виде отдельных проводников с током или пучков заряженных частиц), но и большое число микротоков IiМИКРО (электронных орбит атомов), пронизывающих эту же поверхность:
 = m0
= m0 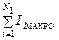 + m0
+ m0 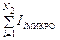 . (15.7)
. (15.7)
Расчёт слагаемого  выполняется по схеме, которая была нами опробована при обсуждении формулировки теоремы Гаусса для электрического поля в среде. На рис. 15.6 изображён малый участок контура dl, который, в силу малости, можно считать прямым. Сама поверхность, натянутая на контур, находится слева от этого участка; очевидно, что вклад в сумму микротоков дадут лишь те из них, которые пронизывают эту поверхность лишь один раз. Они сосредоточены в прилежащей к рассматриваемому участку dl области (наклонного цилиндра) объёмом dV = Sdl×cosa. (здесь S – площадь отдельного витка-микротока, a – угол между образующей цилиндра и перпендикуляром
выполняется по схеме, которая была нами опробована при обсуждении формулировки теоремы Гаусса для электрического поля в среде. На рис. 15.6 изображён малый участок контура dl, который, в силу малости, можно считать прямым. Сама поверхность, натянутая на контур, находится слева от этого участка; очевидно, что вклад в сумму микротоков дадут лишь те из них, которые пронизывают эту поверхность лишь один раз. Они сосредоточены в прилежащей к рассматриваемому участку dl области (наклонного цилиндра) объёмом dV = Sdl×cosa. (здесь S – площадь отдельного витка-микротока, a – угол между образующей цилиндра и перпендикуляром  к его основанию). Если концентрация микротоков равна n, то всего их в этой области dN2 = nSdl×cosa штук, и их сумма вычисляется, как
к его основанию). Если концентрация микротоков равна n, то всего их в этой области dN2 = nSdl×cosa штук, и их сумма вычисляется, как
I×dN2 = I×nSdl×cosa = n×IS×dl×cosa = n×pm×dl×cosa = Jdl×cosa = ( 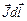 ).
).

В приведённых выкладках использовано то, что pm = IS (формула 15.2) и то, что J = n×pm (формула 15.6).
Последняя запись позволяет заменить суммирование микротоков в формуле (15.7) на их интегрирование вдоль всего выбираемого контура:
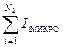 =
=  .
.
Разделив обе части выражения (15.7) на одну и ту же константу m0 и объединив интегралы (они берутся по одному и тому же контуру, а, значит, это можно сделать), получаем:
 =
= 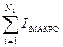 . (15.8)
. (15.8)
Введём обозначение. Комбинация векторов  и
и  вида
вида
 =
= 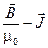 (15.9)
(15.9)
называется вектором напряжённости магнитного поля. В СИ напряжённость магнитного поля, как и намагниченность, измеряется в амперах на метр (А×м-1).
Теперь теорему о циркуляции для магнитного поля в веществе можно сформулировать следующим образом: циркуляция вектора напряжённости магнитного поля по произвольному замкнутому контуру равна алгебраической сумме макротоков, которые пронизывают поверхность, мысленно натянутую на этот контур,
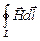 =
= 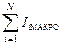 . (15.10)
. (15.10)
Теорему о циркуляции вектора напряжённости магнитного поля называют также законом полного тока.
15.2.3 Связь векторов  ,
,  и
и  . Виды магнетиков.
. Виды магнетиков.
Использованный нами подход для учёта вклада микротоков в создание общего магнитного поля в веществе сходен с тем, который был применён ранее при рассмотрении теоремы Гаусса для электрического поля. Напомним: с целью учёта вклада полей отдельных молекул (электрических диполей) в создание общего электрического поля нами был также введён вспомогательный вектор (вектор электрического смещения),  = e0
= e0 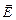 +
+ 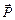 , после чего в формулировке самой теоремы стали фигурировать только свободные (а не связанные с диполями) заряды. Далее мы учли, что
, после чего в формулировке самой теоремы стали фигурировать только свободные (а не связанные с диполями) заряды. Далее мы учли, что 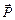 = e0k
= e0k 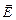 , где k – диэлектрическая восприимчивость вещества, в результате чего получили:
, где k – диэлектрическая восприимчивость вещества, в результате чего получили:  = e0(1 + k)
= e0(1 + k) 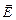 , или
, или  = ee0
= ee0 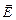 .
.
Применим подобные рассуждения и в случае магнитного поля.
Поскольку ориентация магнитных моментов отдельных микротоков определяется индукцией внешнего поля (см. рис. 15.4), то и их векторная сумма также зависит от  , то есть
, то есть  ~
~  . Обычно, однако, вектор
. Обычно, однако, вектор  связывают не с индукцией магнитного поля, а с его напряжённостью
связывают не с индукцией магнитного поля, а с его напряжённостью  , записывая эту связь в виде
, записывая эту связь в виде
 = c
= c  , (15.11)
, (15.11)
при этом коэффициент пропорциональности c называют магнитной восприимчивостью вещества.
Используя соотношение (15.9), можно осуществить следующие выкладки:  =
= 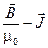 =
=  - c
- c  , или
, или  = m0(1 + c)
= m0(1 + c)  . Если теперь ввести обозначение 1 + c = m, то связь векторов
. Если теперь ввести обозначение 1 + c = m, то связь векторов  и
и  приобретает вид:
приобретает вид:
 = m0m
= m0m  , (15.12)
, (15.12)
где коэффициент m называемся магнитной проницаемостью вещества. Так же, как и диэлектрическая проницаемость e, магнитная проницаемость является безразмерной величиной и зависит от свойств вещества.
Диэлектрическая проницаемость e всегда больше единицы; в отличие от неё магнитная проницаемость m может оказаться меньше единицы. Это связано с тем, что диэлектрическая восприимчивость всегда положительна, в то время как магнитная восприимчивость c оказывается отрицательной у большого числа веществ, относящихся к классу диамагнетиков. Именно по этому параметру и производится классификация магнетиков:
- если ½c½ << 1 и при этом c > 0 (обычно c » 10-5 - 10-4), то такие вещества являются парамагнетиками (типичный пример – щелочные металлы), они слабо реагируют на внешнее магнитное поле, втягиваясь в область с повышенной магнитной индукцией;
- если ½c½ << 1, но при этом c < 0 (обычно c » 10-6 - 10-5), то такие вещества являются диамагнетиками (типичный пример – инертные газы), они также слабо реагируют на внешнее магнитное поле, но выталкиваются из него;
- магнитная восприимчивость ферромагнетиков не только положительна и весьма велика (c >> 1 и может достигать 103 - 104), но она, к тому же, не является константой, c = c(H), то есть зависит от напряжённости магнитного поля.
15.2.4 Некоторые примеры
- К диамагнетикам относятся инертные газы, азот, водород, кремний, фосфор, висмут, цинк, медь, золото, серебро, а также многие другие, как органические, так и неорганические, соединения. Человек в магнитном поле ведет себя как диамагнетик.
- Идеальными диамагнетиками являются сверхпроводники, их магнитная восприимчивость c = - 1, то есть внешнее магнитное поле внутри них полностью экранируется.
- Парамагнетиками являются щелочные и щелочно-земельные металлы, некоторые переходные металлы, соли железа, кобальта, никеля, редкоземельных металлов, кислород, окись азота.
- Примеры ферромагнетиков: железо, никель, кобальт, их соединения и сплавы, некоторые сплавы марганца, серебра, алюминия и др. При низких температурах некоторые редкоземельные элементы – гадолиний, тербий, диспрозий, гольмий, эрбий, тулий.
15.2.5 Вопросы для повторения
1. Выведите формулу для расчёта работы по перемещению прямого проводника с током в однородном магнитном поле.
2. Что называется магнитным моментом витка с током? Как ведёт себя виток в однородном и неоднородном магнитных полях?
3. Какой принцип лежит в основе работы электромотора?
4. Что называется намагниченностью вещества  ? В каких единицах намагниченность измеряется в СИ?
? В каких единицах намагниченность измеряется в СИ?
5. Что называется вектором напряжённости магнитного поля  ? В каких единицах напряжённость магнитного поля измеряется в СИ?
? В каких единицах напряжённость магнитного поля измеряется в СИ?
6. Сформулируйте закон полного тока. Продемонстрируйте, как, пользуясь этим законом, можно вывести формулу для индукции магнитного поля, создаваемого прямым тонким проводником с током на некотором расстоянии от него.
7. Какие классы магнетиков вам известны? По какому параметру они отличаются друг от друга?
Дата добавления: 2020-02-05; просмотров: 625;











