Лекция 14 МАГНИТНОЕ ПОЛЕ. ЧАСТЬ II
14.1 ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ (Часть II)
14.1.1 Действие магнитного поля на движущийся заряд. Сила Лоренца. Ускорители заряженных частиц
14.1.2 Эффект Холла. Использование эффекта Холла для определения знака и концентрации носителей заряда
14.1.3 Теорема о циркуляции вектора  . Примеры применения теоремы
. Примеры применения теоремы
14.1.4 Теорема Гаусса для магнитного поля
Некоторые примеры
Вопросы для повторения
14.1 ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ (Часть II)
14.1.1 Действие магнитного поля на движущийся заряд.
Сила Лоренца. Ускорители заряженных частиц
Итак, на проводник длиной l, по которому идёт ток I и который находится в магнитном поле с индукцией B, действует сила Ампера FA, вычисляемая по формуле FA = IlBsina, где a – угол между направлением тока и вектором магнитной индукции. Если же тока нет, то сила Ампера не возникает. Этот факт заставляет предположить, что магнитное поле действует лишь на движущиеся заряды (в металлах – на электроны), а на неподвижные (на ионы кристаллической решётки, испытывающие только хаотические тепловые колебания около положения равновесия) влияния не оказывает. Поэтому давайте получим формулу для вычисления силы, действующей в магнитном поле на один движущийся заряд.
Согласно определению, сила постоянного тока I = 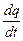 =
=  , где Dq – общий заряд, который переносится силами поля за время Dt. Если зарядов N штук, и величина каждого равна q, то Dq = Nq, и формулу для силы Ампера можно переписать в виде
, где Dq – общий заряд, который переносится силами поля за время Dt. Если зарядов N штук, и величина каждого равна q, то Dq = Nq, и формулу для силы Ампера можно переписать в виде
F =  lBsina = Nq
lBsina = Nq  Bsina.
Bsina.
Поскольку Dt – это время, за которое заряды преодолевают расстояние l под действием сил поля, то дробь l/Dt фактически равна их дрейфовой скорости u, направление которой к тому же (в случае положительных зарядов) совпадает с направлением протекания тока. Сказанное позволяет сделать следующий шаг:
F = NquBsina, или 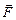 = Nq[
= Nq[ 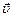
 ].
].
Но 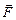 – сила, действующая на все N зарядов, а на каждый из них по отдельности действует сила FЛ, в N раз меньшая:
– сила, действующая на все N зарядов, а на каждый из них по отдельности действует сила FЛ, в N раз меньшая:
 = q[
= q[ 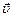
 ]. (14.1)
]. (14.1)
Эта сила носит название силы Лоренца.
Данная сила действует на любой заряд, движущийся в магнитном поле. Если же кроме магнитного поля на заряд действует ещё и электрическое, то
 = q[
= q[ 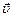
 ] + q
] + q 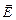 . (14.2)
. (14.2)
Определить направление силы Лоренца по формуле (14.1) можно, используя правило левой руки. Однако, следует помнить, что это правило в математике применяется лишь для определения направления векторного произведения (в нашем случае – произведения [ 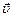
 ]). Если заряд q положителен, то направление
]). Если заряд q положителен, то направление  совпадёт с направлением этого произведения, если заряд q имеет знак «минус» (как, например, у электрона), то сила Лоренца будет направлена в сторону, противоположную той, которая определялась про правилу левой руки.
совпадёт с направлением этого произведения, если заряд q имеет знак «минус» (как, например, у электрона), то сила Лоренца будет направлена в сторону, противоположную той, которая определялась про правилу левой руки.
Особенностью векторного произведения является то, что его результат (в нашем случае вектор  ) оказывается перпендикулярным обоим сомножителям (у нас – векторам
) оказывается перпендикулярным обоим сомножителям (у нас – векторам 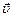 и
и  ). Если при этом сами вектора
). Если при этом сами вектора 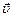 и
и  взаимно перпендикулярны, то заряд будет двигаться в магнитном поле по окружности.
взаимно перпендикулярны, то заряд будет двигаться в магнитном поле по окружности.
На рис. 14.1 изображены траектории движения в однородном магнитном поле одинаковых по массе, но имеющих заряды +q и -q, частиц, влетевших с одинаковой скоростью в поле пер 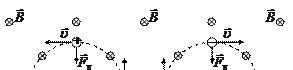 пендикулярно его силовым линиям (на рисунке они направлены «от нас»). Если скорость влетающего в поле заряда имеет компоненту
пендикулярно его силовым линиям (на рисунке они направлены «от нас»). Если скорость влетающего в поле заряда имеет компоненту 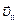 , параллельную силовым линиям, траекторией заряда окажется винтовая спираль. Вдоль оси спирали заряд будет двигаться равномерно со скоростью
, параллельную силовым линиям, траекторией заряда окажется винтовая спираль. Вдоль оси спирали заряд будет двигаться равномерно со скоростью 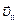 , но одновременно под действием силы Лоренца он станет вращаться вокруг оси спирали с постоянной линейной скоростью
, но одновременно под действием силы Лоренца он станет вращаться вокруг оси спирали с постоянной линейной скоростью 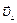 (здесь
(здесь 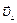 – компонента скорости, перпендикулярная вектору
– компонента скорости, перпендикулярная вектору  ). При этом сила Лоренца FЛ = q
). При этом сила Лоренца FЛ = q  B.
B.
Возможность отклонять пучки заряженных частиц от первоначального направления распространения с помощью магнитного поля широко используется на практике. Системы такого отклонения обычно оказываются более компактными, чем те, в которых отклонение обеспечивается электрическими полями. Типичный пример использования этого явления – электронно-лучевые трубки (кинескопы) телевизоров. Электроны, испускаемые нагретым катодом, после ускорения электрическим полем отклоняются магнитными полями соленоидов системы вертикальной и горизонтальной развёртки. В результате электронный луч попадает в заданные точки экрана, заставляя светиться нанесённый на него люминофор: возникает изображение.
Принцип организации движения зарядов не по прямой, а по окружности, используется в ускорителях заряженных частиц (в том числе – в запущенном недавно в Европейском центре ядерных исследований Большом адронном коллайдере). Непосредственно для ускорения частиц до больших скоростей применяется электрическое поле, силы которого совершают работу по перемещению зарядов и, тем самым, сообщают им требуемую кинетическую энергию. Однако за время разгона частицы успевает пройти большое расстояние, а построить требуемый для этого прямой, достаточно длинный тоннель, из которого, к тому же, должен быть откачен воздух (такая конструкция носит название «линейный ускоритель»), технически весьма сложно (и даже практически невозможно, если длина тоннеля должна превышать несколько сотен метров). Но использование магнитного поля позволяет «свернуть» прямую траекторию ускоряемой заряженной частицы в окружность или расширяющуюся спираль. Примером устройства данного типа является циклотрон.
Циклотрон состоит из двух металлических коробов (они называются «дуанты»), форма каждого из которых близка форме половины цилиндра, разрезанного на две равные части вдоль оси симметрии. Дуанты внутри пустые, на них может создаваться разность потенциалов как одного, так и другого знаков, причём каждый находится в магнитном поле, силовые линии которого перпендикулярны его основаниям (рис. 14.2.а).
Дуанты разведены друг от друга на некоторое расстояние; если ввести в зазор вблизи центра системы заряженную частицу и создать между дуантами ускоряющую разность потенциалов j1 - j2, частица начнёт ускоряться. В момент влёта частицы внутрь первого дуанта она уже будет иметь некоторую скорость, однако там на неё будет действовать сила Лоренца, и траектория частицы искривится. Описав полуокружность, частица вылетит из дуанта, но к этому времени полярность дуантов меняют, и частица вновь ускоряется в зазоре между ними. Она влетает уже во второй дуант (её скорость стала больше), внутри него вновь испытывает действие силы Лоренца, и, описав полуокружность, вылетает из него. К этому времени полярность дуантов меняют вновь: происходит новое ускорение частицы, затем имеет место новый поворот магнитным полем и т.д. (рис. 14.2.б).

Поскольку скорость частицы всё время возрастает, её траекторией оказывается уже не окружность, а расширяющаяся спиралевидная кривая, и когда её радиус достигнет размера установки, частица вылетает из дуанта в специальное окно: поставленная цель по разгону частицы до нужной скорости выполнена.
На практике, конечно, всё обстоит не так просто: следует точно согласовать моменты переключения полярности дуантов с моментами вылета частицы из очередного из них, учесть эффект увеличения релятивистской массы частицы при больших скоростях и т.д. Именно поэтому разгон заряженных частиц до скоростей, приближающихся к скорости света, происходит на установках, которые имеют уже другую конструкцию – синхротронах, синхрофазотронах и др. Однако сам принцип превращения прямолинейной траектории движения разгоняемой заряженной частицы в окружность или расширяющуюся спираль остаётся тем же: это делается с помощью силы Лоренца.
14.1.2 Эффект Холла. Использование эффекта Холла
для определения знака и концентрации носителей заряда
Ещё одним эффектом, в котором проявляется действие силы Лоренца, является эффект Холла. Эффект заключается в возникновении поперечной разности потенциалов в проводнике, по которому идёт электрический ток и который помещён в магнитное поле.

Рассмотрим образец, по которому идёт электрический ток – результат движения положительных зарядов (например, протонов), рис. 14.3.а). Если образец помещён в магнитное поле, силовые линии которого перпендикулярны вектору плотности тока (совпадающему по направлению с вектором дрейфовой скорости зарядов), то на него будет действовать сила Лоренца (на рисунке  направлена на нас). На передней грани образца начнёт накапливаться положительный заряд, задняя грань будет заряжена отрицательно.
направлена на нас). На передней грани образца начнёт накапливаться положительный заряд, задняя грань будет заряжена отрицательно.
Одновременно с накоплением зарядов в образце возникнет электрическое поле, которое действует на положительные заряды с силой  , противоположной по направлению силы Лоренца. По мере накопления зарядов эта сила возрастает до тех пор, пока не сравняется по величине с
, противоположной по направлению силы Лоренца. По мере накопления зарядов эта сила возрастает до тех пор, пока не сравняется по величине с  . После этого накопление заряда на передней и задней гранях прекращается и новые заряды, попадающие в образец, движутся прямолинейно. В итоге передняя грань приобретает потенциал +j1, задняя – потенциал -j2; возникающая поперечная разность потенциалов называется «холловской».
. После этого накопление заряда на передней и задней гранях прекращается и новые заряды, попадающие в образец, движутся прямолинейно. В итоге передняя грань приобретает потенциал +j1, задняя – потенциал -j2; возникающая поперечная разность потенциалов называется «холловской».
Получим выражение для разности j1 - j2.
В состоянии, когда действие сил  и
и  уравновешивается с учётом того, что FЛ = quB, а FЭ = qE, где E – напряжённость возникшего поперечного электрического поля, можно записать: quB = qE, или uB = E.
уравновешивается с учётом того, что FЛ = quB, а FЭ = qE, где E – напряжённость возникшего поперечного электрического поля, можно записать: quB = qE, или uB = E.
Электрическое поле в пространстве между передней и задней гранями образца (грани параллельны) можно считать однородным, и для него, также, как и для электрического поля внутри плоского конденсатора, можно записать: E =  =
=  . Таким образом, uB =
. Таким образом, uB =  , или j1 - j2 = uBb. Но при выводе формулы закона Ома в дифференциальной форме мы показали, что плотность тока j связана с концентрацией n и скоростью u носителей заряда соотношением j = enu. Полагая, что в нашем случае заряд q равен по величине заряду электрона e = 1,6×10-19 Кл, и выразив скорость носителей заряда u через плотность тока и концентрацию, получим:
, или j1 - j2 = uBb. Но при выводе формулы закона Ома в дифференциальной форме мы показали, что плотность тока j связана с концентрацией n и скоростью u носителей заряда соотношением j = enu. Полагая, что в нашем случае заряд q равен по величине заряду электрона e = 1,6×10-19 Кл, и выразив скорость носителей заряда u через плотность тока и концентрацию, получим:
j1 - j2 =  Bbj. (14.3)
Bbj. (14.3)
Из формулы следует, что, измерив в эксперименте ширину образца b, плотность идущего через него тока j, индукцию магнитного поля B и холловскую разность потенциалов j1 - j2, можно вычислить концентрацию носителей заряда в образце, и даже более того, – исследовать, как меняется эта концентрация в зависимости от тех или иных внешних воздействий (при нагреве, внешней засветке и т.д.). Именно поэтому эффект Холла является мощным инструментом исследования в физике полупроводников и металлов.
Коэффициент, стоящий перед произведением Bbj в формуле (14.3) носит название постоянной Холла и обозначается RХ., в общем случае он отличается от полученной нами дроби  на множитель, по величине, близкий к единице.
на множитель, по величине, близкий к единице.
Помимо концентрации носителей заряда, создающих электрический ток, эффект Холла позволяет определить их знак. Мы уже убедились в том, что если ток создают положительно заряженные носители, потенциал передней грани приобретает знак «плюс». Но если такой же ток создают отрицательно заряженные носители (для этого они должны двигаться в противоположном вектору 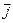 направлении, рис. 14.3.б), то, согласно правилу левой руки, «от нас» будет направлено векторное произведение [
направлении, рис. 14.3.б), то, согласно правилу левой руки, «от нас» будет направлено векторное произведение [ 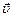
 ]. Сама же сила Лоренца, как результат умножения этого произведения на отрицательный заряд q, как и в первом случае окажется направленной «на нас»: потенциал передней грани образца будет иметь знак «минус».
]. Сама же сила Лоренца, как результат умножения этого произведения на отрицательный заряд q, как и в первом случае окажется направленной «на нас»: потенциал передней грани образца будет иметь знак «минус».
Таким образом, используя эффект Холла, можно определить, например, каким типом электропроводности (p- или n-) характеризуется полупроводник.
В заключение отметим: сила Лоренца разделяет электрические заряды, отклоняя заряды одного знака в одну сторону, а другого – в противоположную, что позволяет использовать её в качестве сторонней для создания источников э. д. с. Как мы увидим далее, именно это свойство силы Лоренца лежит в основе явления электромагнитной индукции.
14.1.3 Теорема о циркуляции вектора  . Примеры применения теоремы
. Примеры применения теоремы
Расчёт сил, действующих в магнитном поле на проводники с током и движущиеся заряды, требует умения вычислять значение индукции магнитного поля в любой точке пространства. Это можно сделать, используя закон Био-Савара-Лапласа, однако, в ряде случаев, для расчётов удобно применять другой подход, основанный на использовании теоремы о циркуляции вектора  . Данный подход во многом схож с тем, который лежит в основе вычисления напряженности электрического поля путём применения теоремы Гаусса.
. Данный подход во многом схож с тем, который лежит в основе вычисления напряженности электрического поля путём применения теоремы Гаусса.
Для начала введём определение.
Если в пространстве, каждой точке которого соответствует некоторый вектор 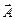 , выбрать замкнутый контур L и затем начать обходить этот контур в каком-то направлении, то каждому малому элементу длины этого контура
, выбрать замкнутый контур L и затем начать обходить этот контур в каком-то направлении, то каждому малому элементу длины этого контура  (направление вектора совпадает с направлением обхода) можно сопоставить скалярное произведение (
(направление вектора совпадает с направлением обхода) можно сопоставить скалярное произведение ( 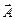
 ) = Adlcosa, где A – величина вектора
) = Adlcosa, где A – величина вектора 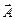 в области выбранного вектора
в области выбранного вектора  , а a – угол между этими векторами. Просуммировав такие произведения вдоль всего контура, мы получаем интеграл (обозначим его буквой G), который называется циркуляцией вектора
, а a – угол между этими векторами. Просуммировав такие произведения вдоль всего контура, мы получаем интеграл (обозначим его буквой G), который называется циркуляцией вектора 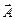 по контуру L:
по контуру L:
G = 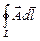 . (14.4)
. (14.4)
После того, как мы записали определение циркуляции вектора[10], сформулируем теорему, вынесенную в заглавие параграфа.
Циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна умноженной на магнитную постоянную m0 алгебраической сумме токов, которые пронизывают поверхность, мысленно натянутую на этот контур:
 = m0
= m0 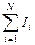 . (14.5)
. (14.5)
При вычислении суммы следует учитывать направление обхода контура: те токи, которые пронизывают поверхность, мысленно натянутую на контур в направлении, совпадающем с направлением хода винта (буравчика), вращаемого в сторону обхода, берутся со знаком «плюс», те, которые идут в противоположном направлении, – со знаком «минус».
Точно так же, как и в случае теоремы Гаусса для электрического поля, в которой речь шла о произвольной замкнутой поверхности, выбираемый контур обхода может иметь любую форму, и именно поэтому его выбирают таким, чтобы можно было легко взять интеграл и, тем самым, получить формулу для расчёта индукции B в заданной точке пространства.
Рассмотрим два примера.
а) Расчёт индукции магнитного поля прямого бесконечно длинного тонкого проводника с током
Выполним шаги, аналогичные тем, которые мы делали в случае использования теоремы Гаусса для электрического поля.
– Начертим рисунок с изображением проводника с током и силовых линий создаваемого им магнитного поля (рис. 14.4).
 – Укажем на рисунке точку, в которой мы будем рассчитывать величину индукции магнитного поля, и проведём сквозь эту точку силовую линию (на рис. 14.4. это точка А).
– Укажем на рисунке точку, в которой мы будем рассчитывать величину индукции магнитного поля, и проведём сквозь эту точку силовую линию (на рис. 14.4. это точка А).
– Выберем замкнутый контур, форма которого соответствовала бы симметрии задачи; контур должен проходить через нужную нам точку А (на рис. 14.4. это окружность радиусом R, плоскость которой перпендикулярна проводнику с током, проходящему через центр этой окружности).
– Посчитаем циркуляцию вектора индукции магнитного поля по выбранному контуру. Обход совершим по направлению силовых линий, тогда в формуле (14.5) ток можно будет брать со знаком «плюс».
Во всех точках выбранный нами контур совпадает с одной и той же силовой линией и согласуется с ней по направлению обхода, поэтому угол a между векторами  и
и  везде равен нулю. Кроме того, в силу симметрии контура (все участки которого находятся на равном расстоянии от проводника с током) во всех его точках величина индукции одинакова, и множитель B можно вынести за знак интеграла. Учтём также, что, по определению интеграла,
везде равен нулю. Кроме того, в силу симметрии контура (все участки которого находятся на равном расстоянии от проводника с током) во всех его точках величина индукции одинакова, и множитель B можно вынести за знак интеграла. Учтём также, что, по определению интеграла,  = 2pR. Сказанное означает:
= 2pR. Сказанное означает:
 =
=  =
=  = B
= B  = 2pRB.
= 2pRB.
– Определим теперь, какой суммарный ток пронизывает поверхность, мысленно натянутую на выбранный контур, после чего применить теорему о циркуляции вектора  .
.
В нашем случае речь идёт только об одном токе I, следовательно, циркуляция вектора  должна просто равняться произведению m0I, то есть,
должна просто равняться произведению m0I, то есть,
2pRB = m0I.
Сказанное означает, что индукция магнитного поля, создаваемого прямым тонким бесконечно длинным проводником с током I на расстоянии R от него, рассчитывается по формуле:
B = 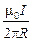 . (14.6)
. (14.6)
б) Расчёт индукции магнитного поля тороида (и бесконечно длинного соленоида) с током
Тороид представляет собой тороидальный (имеющий «форму бублика») сердечник, изготовленный из немагнитного материала, на который виток к витку плотно навит провод в тонкой изоляционной оболочке. На рис. 14.5.а) показан вид такого объекта сверху; для того, чтобы не загромождать чертёж, витки провода изображены лишь в его левой части. Заметим: тороидом бесконечно большого радиуса R можно считать бесконечно длинный соленоид.
Всё пространство вокруг проводов с током I, идущим по тороиду, можно разбить на три области. Область I соответствует точкам, лежащим вне тороида, область II – точкам, которые находятся в его «дырке» и область III, лежащая в «теле» сердечника тороида (рис. 14.5.б). Определим, какова индукция магнитного поля в этих областях на примере точек A, A¢ и A¢¢.
Проведём через точку A замкнутый контур I, окружающий тороид. Поверхность, мысленно натянутая на тот контур, пересекается каждым витком дважды (рис. 14.5.в), поэтому алгебраическая сумма токов, идущих по виткам и пронизывающих эту поверхность равна нулю, какой бы формы контур мы ни выбирали. Но если при любом выборе формы контура интеграл по нему равен нулю, то это означает, что под знаком интеграла также стоит ноль. Так как  явно не ноль, это означает, что вне тороида индукция магнитного поля равна нулю, то есть вне тороида маг
явно не ноль, это означает, что вне тороида индукция магнитного поля равна нулю, то есть вне тороида маг
 |
нитного поля нет.
Аналогичная ситуация имеет место и в области II. Какой бы формы контур (овальный, треугольный, четырёхугольный и т. д.), проходящий через точку A¢ мы ни выбирали, циркуляция вектора  по нему будет равна нулю, так как поверхности, натянутые на каждый из этих контуров токами вообще не пересекаются. И снова, - если для любого контура интеграл равен нулю, следовательно, дело в подынтегральном выражении – оно (точнее вектор
по нему будет равна нулю, так как поверхности, натянутые на каждый из этих контуров токами вообще не пересекаются. И снова, - если для любого контура интеграл равен нулю, следовательно, дело в подынтегральном выражении – оно (точнее вектор  ) тождественно равно нулю: магнитного поля нет и в области II.
) тождественно равно нулю: магнитного поля нет и в области II.
Но в области III ситуация качественно иная: поверхность, натянутая на контур - окружность, которая совпадает со средней линией тороида, пронизывается каждым витком только один раз, и все соответствующие токи идут в одном направлении. Ранее силовые линии внутри соленоида мы уже рисовали; с учётом того, что и внутри тороида силовые линии на каждом участке параллельны контуру обхода – окружности, можно записать, что угол a между  и
и  в любом месте равен нулю. Кроме того, в силу симметрии контура и тороида, индукция B должна быть одинакова в любой точке контура, длина которого равна 2pR:
в любом месте равен нулю. Кроме того, в силу симметрии контура и тороида, индукция B должна быть одинакова в любой точке контура, длина которого равна 2pR:
 =
=  =
=  = B
= B  = 2pRB.
= 2pRB.
Сумма токов, пронизывающих поверхность, мысленно натянутую на выбранный контур, равна NI, где N – общее число витков проволоки. Сказанное означает: внутри тороида (так же, как и внутри бесконечно длинного соленоида)
B =  m0I = m0nI, (14.7)
m0I = m0nI, (14.7)
где n – число витков на единицу длины тороида.
Формулы (14.6) и (14.7) совпадают с формулами, которые можно получить для этих же объектов, используя закон Био-Савара-Лапласа (см. предыдущую лекцию).
14.1.4 Теорема Гаусса для магнитного поля
Помимо теоремы о циркуляции вектора  в теории магнетизма имеется своя теорема Гаусса, которая также касается потока вектора, являющегося силовой характеристикой поля (в данном случае – магнитного). Речь идёт о потоке вектора магнитной индукции или о магнитном потоке.
в теории магнетизма имеется своя теорема Гаусса, которая также касается потока вектора, являющегося силовой характеристикой поля (в данном случае – магнитного). Речь идёт о потоке вектора магнитной индукции или о магнитном потоке.
По определению магнитным потоком FМ через некоторую поверхность S называется интеграл вида
FМ = 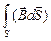 . (14.8)
. (14.8)
В отличие от потока вектора напряжённости электрического поля магнитный поток в СИ имеет собственную единицу измерения – вебер; 1 Вб = 1 Тл×м2.
В формуле (14.8) поверхность может быть любой, но в теореме Гаусса говорится о замкнутой поверхности. Приведём текст теоремы и соответствующую ей формулу[11].
Поток вектора индукции магнитного поля через произвольную замкнутую поверхность равен нулю:
 = 0. (14.9)
= 0. (14.9)
Напомним: применяя теорему Гаусса для электрического поля, в правую часть формулы следует подставлять алгебраическую сумму электрических зарядов, охватываемых поверхностью. Именно поэтому теорема Гаусса для магнитного поля, согласно которой в правой части формулы должен стоять ноль, иногда интерпретируется, как свидетельство того, что отдельно существующих магнитных «зарядов» (монополей – «северных» и «южных») в природе не существует.
Продемонстрируем справедливость теоремы на простейшем примере, применив её для описания магнитного поля, создаваемого прямым, тонким, бесконечно длинным проводником с током (рис. 14.6).
 – Начертим рисунок, выберем некоторую точку A, находящуюся на расстоянии R от прямого проводника с током, изобразим силовые линии магнитного поля (одна из них проходит через точку A).
– Начертим рисунок, выберем некоторую точку A, находящуюся на расстоянии R от прямого проводника с током, изобразим силовые линии магнитного поля (одна из них проходит через точку A).
– Выберем замкнутую поверхность, форма которой соответствует симметрии задачи; поверхность проходит через выбранную точку А (на рис. 14.6. это цилиндр радиусом R, ось которого совпадает с проводником).
– Посчитаем поток вектора индукции магнитного поля по выбранной поверхности, как сумму интегралов по двум донышкам цилиндра SД1 и SД2, а также по его боковой поверхности SБ. Учтём, что нормали и к донышкам цилиндра и к любому элементу боковой поверхности (например, – в выбранной точке A) перпендикулярны силовым линиям магнитного поля, поэтому:
FМ =  =
=  +
+  +
+  =
=
=  +
+  +
+  = 0.
= 0.
Таким образом, магнитный поток через выбранную нами замкнутую поверхность действительно равен нулю: утверждение, высказанное в виде теоремы Гаусса для магнитного поля, справедливо.
Некоторые примеры
- Диаметр первого циклотрона (1931 г.) составлял 25 см. Диаметр Серпуховского ускорителя равен примерно 1,5 км, средний диаметр кольца Большого адронного коллайдера превышает 8 км.
- Поскольку величина холловской разности потенциалов зависит от индукции внешнего магнитного поля, создаваемого, в частности проводниками, по которым идёт электрический ток, то это позволяет создавать на основе датчиков Холла бесконтактные измерители силы тока в пределах от десятков миллиампер до нескольких тысяч ампер.
- На основе эффекта Холла созданы (и предлагаются к продаже многими фирмами) датчики тока, индукции магнитного поля, положения, перемещения, расхода, угла поворота, частоты вращения и др.; устройства блокировки дверей, считыватели магнитных карточек или ключей, датчики систем зажигания автомобилей, бесконтактные реле и т. д.
Вопросы для повторения
1. Пользуясь формулой закона Ампера, выведите формулу для силы Лоренца.
2. Опишите принцип работы циклотрона.
3. В чём заключается эффект Холла? Как с его помощью можно определить концентрацию и знак носителей заряда в веществе?
4. Что называется циркуляцией вектора  ?
?
5. Сформулируйте теорему о циркуляции вектора магнитной индукции и приведите пример её применения для вычисления индукции магнитного поля, создаваемого прямым бесконечным проводником с током.
6. Сформулируйте теорему о циркуляции вектора магнитной индукции и приведите пример её применения для вычисления индукции магнитного поля, создаваемого тороидом.
Дата добавления: 2020-02-05; просмотров: 734;











