Лекция 16 МАГНИТНОЕ ПОЛЕ. ЧАСТЬ IV
16.1 МАГНИТОЕ ПОЛЕ В ВЕЩЕСТВЕ
16.1.1 Парамагнетизм
16.1.2 Прецессия электронных орбит в атоме. Диамагнетизм
16.1.3 Ферромагнетизм. Петля гистерезиса
Некоторые примеры
Вопросы для повторения
16.1 МАГНИТОЕ ПОЛЕ В ВЕЩЕСТВЕ
16.1.1 Парамагнетизм
Итак, все вещества по их магнитным свойствам можно разделить на несколько классов, среди которых мы выделили парамагнетики (их магнитная восприимчивость ½c½ << 1 и при этом c > 0), диамагнетики (½c½ << 1, но при этом c < 0) и ферромагнетики (c >> 0, причём c = c(H)). Рассмотрим, чем обусловлены магнитные свойства этих веществ.
Как мы уже говорили, движение электрона по орбите вокруг ядра можно интерпретировать, как протекание микротока, имеющего некоторый магнитный момент  , связь которого с орбитальным моментом импульса описывается гиромагнитным отношением
, связь которого с орбитальным моментом импульса описывается гиромагнитным отношением  = -
= -  . Кроме того, как следует из уравнений квантовой механики, каждый электрон обладает собственным моментом импульса
. Кроме того, как следует из уравнений квантовой механики, каждый электрон обладает собственным моментом импульса 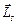 , спином (поначалу его связывали с вращением электрона вокруг собственной оси, но такое представление оказалось неверным) и соответствующим ему собственным (спиновым) магнитным моментом
, спином (поначалу его связывали с вращением электрона вокруг собственной оси, но такое представление оказалось неверным) и соответствующим ему собственным (спиновым) магнитным моментом  . Связь
. Связь  с
с 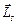 описывается своим гиромагнитным отношением:
описывается своим гиромагнитным отношением: 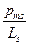 = -
= -  . Более того, собственными (спиновыми) магнитными моментами обладают также протоны и нейтроны, входящие в состав ядра. Сказанное означает, что общий магнитный момент
. Более того, собственными (спиновыми) магнитными моментами обладают также протоны и нейтроны, входящие в состав ядра. Сказанное означает, что общий магнитный момент 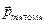 атома, позволяющий интерпретировать его, как некий единый микроток, должен являться суммой векторов
атома, позволяющий интерпретировать его, как некий единый микроток, должен являться суммой векторов  всех электронов и
всех электронов и  всех электронов, протонов и нейтронов, входящих в состав атома:
всех электронов, протонов и нейтронов, входящих в состав атома:
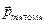 =
= 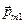 +
+ 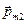 + … +
+ … + 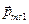 +
+  + … (16.1)
+ … (16.1)
Если 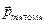 не равен нулю, то отличной от нуля является и намагниченность
не равен нулю, то отличной от нуля является и намагниченность  =
=  (здесь k – номер атома в малом объёме DV материала), а поскольку микротоки в магнитном поле стремятся развернуться так, чтобы их
(здесь k – номер атома в малом объёме DV материала), а поскольку микротоки в магнитном поле стремятся развернуться так, чтобы их  совпадали по направлению с векторами
совпадали по направлению с векторами  и
и  , то магнитная восприимчивость c (коэффициент пропорциональности в формуле
, то магнитная восприимчивость c (коэффициент пропорциональности в формуле  = c
= c  ) оказывается положительной. Из-за того, что магнитные моменты электронов протонов и нейтронов направлены в разные стороны суммарный магнитный момент атома оказывается малым, не очень большой оказывается и намагниченность, поэтому ½c½ << 1. Вещества, магнитные моменты атомов
) оказывается положительной. Из-за того, что магнитные моменты электронов протонов и нейтронов направлены в разные стороны суммарный магнитный момент атома оказывается малым, не очень большой оказывается и намагниченность, поэтому ½c½ << 1. Вещества, магнитные моменты атомов 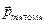 которых в отсутствие внешних воздействий не равны нулю и при этом не оказывают влияния друг на друга, являются парамагнетиками, для них обычно c » 10-5 - 10-4.
которых в отсутствие внешних воздействий не равны нулю и при этом не оказывают влияния друг на друга, являются парамагнетиками, для них обычно c » 10-5 - 10-4.
 Очевидно: чем больше напряжённость внешнего поля
Очевидно: чем больше напряжённость внешнего поля  , тем больше атомов разворачивает свои магнитные моменты по полю (их полномы развороту мешают тепловые колебания атомов, их взаимодействие друг с другом – аналог трения). Зависимость J(H) оказывается линейной, правда, лишь в области в не слишком больших значениях напряжённости магнитного поля. Возрастание H может привести к выходу кривой J(H) на насыщение (рис. 16.1), которое наступит, когда по полю развернутся магнитные моменты всех атомов.
, тем больше атомов разворачивает свои магнитные моменты по полю (их полномы развороту мешают тепловые колебания атомов, их взаимодействие друг с другом – аналог трения). Зависимость J(H) оказывается линейной, правда, лишь в области в не слишком больших значениях напряжённости магнитного поля. Возрастание H может привести к выходу кривой J(H) на насыщение (рис. 16.1), которое наступит, когда по полю развернутся магнитные моменты всех атомов.
То, что тепловые колебания атомов мешают упорядочению их магнитных моментов, находит своё отражение в законе Кюри, согласно которому магнитная восприимчивость парамагнетиков обратно пропорциональна термодинамической температуре:
c = 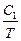 , (16.2)
, (16.2)
где C1 – некоторая постоянная для данного вещества величина (постоянная Кюри).
Парамагнитными свойствами может обладать также газ свободных электронов в твёрдом теле. Это происходит в случае, если число электронов, обладающих проекцией собственного (спинового) магнитного момента, направленной по полю, заметно превышает число электронов, собственный магнитный момент которых направлен против поля. В отличие от парамагнетизма электронов в атоме, парамагнетизм свободных носителей заряда не зависит от температуры.
Типичным примером веществ – парамагнетиков являются щелочные металлы.
16.1.2 Прецессия электронных орбит в атоме. Диамагнетизм
Может оказаться, что суммарный магнитный момент атома 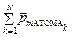 какого-либо вещества равен нулю, тогда нулю окажется и его намагниченность J. Казалось бы, это означает, что нулевой должна оказаться и магнитная восприимчивость c, однако этого не наблюдается, поскольку в таких условиях наблюдается эффект, о котором пока мы не говорили: эффект прецессии электронных орбит в магнитном поле.
какого-либо вещества равен нулю, тогда нулю окажется и его намагниченность J. Казалось бы, это означает, что нулевой должна оказаться и магнитная восприимчивость c, однако этого не наблюдается, поскольку в таких условиях наблюдается эффект, о котором пока мы не говорили: эффект прецессии электронных орбит в магнитном поле.
Рассмотрим электрон, движущийся по круговой орбите вокруг ядра. Движению этого электрона соответствуют орбитальный момент импульса  и орбитальный же магнитный момент
и орбитальный же магнитный момент  , которые направлены в противоположные стороны (рис. 16.2).
, которые направлены в противоположные стороны (рис. 16.2).
 В однородном магнитном поле, силовые линии которого на рисунке направлены вверх, вектор
В однородном магнитном поле, силовые линии которого на рисунке направлены вверх, вектор  стремится развернуться по полю, и это означает, что на электронную орбиту действует момент сил
стремится развернуться по полю, и это означает, что на электронную орбиту действует момент сил 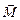 , направленный вглубь рисунка. Однако, согласно основному закону динамики вращательного движения,
, направленный вглубь рисунка. Однако, согласно основному закону динамики вращательного движения, 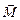 =
= 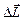 /Dt, то есть к моменту импульса
/Dt, то есть к моменту импульса  , лежащему в плоскости рисунка должен добавиться вектор
, лежащему в плоскости рисунка должен добавиться вектор 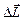 , направленный туда же, что и вектор
, направленный туда же, что и вектор 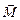 , то есть – вглубь рисунка. Новый момент импульса
, то есть – вглубь рисунка. Новый момент импульса 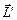 =
=  +
+ 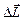 теперь уже не будет лежать в плоскости рисунка, ось вращения повернётся: начнётся прецессия электронной орбиты. Ситуация аналогична той, которую мы рассматривали в механике в случае прецессии гироскопа под действием силы тяжести. Но если в механике всё заканчивалось констатацией возникновения прецессии (того, что ось вращения и сам гироскоп начинают поворачиваться относительно вертикали), то сейчас следует учесть, то, что прецессия электронной орбиты означает возникновение добавочного движения отрицательно заряженной частицы, электрона. Добавочному движению соответствует добавочный ток прецессии IПР, направление которого противоположно направлению движения кончика вектора
теперь уже не будет лежать в плоскости рисунка, ось вращения повернётся: начнётся прецессия электронной орбиты. Ситуация аналогична той, которую мы рассматривали в механике в случае прецессии гироскопа под действием силы тяжести. Но если в механике всё заканчивалось констатацией возникновения прецессии (того, что ось вращения и сам гироскоп начинают поворачиваться относительно вертикали), то сейчас следует учесть, то, что прецессия электронной орбиты означает возникновение добавочного движения отрицательно заряженной частицы, электрона. Добавочному движению соответствует добавочный ток прецессии IПР, направление которого противоположно направлению движения кончика вектора  . Такой ток обладает магнитным моментом
. Такой ток обладает магнитным моментом 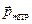 , направленным против вектора
, направленным против вектора  (и, соответственно, – вектора
(и, соответственно, – вектора  ), причём, чем сильнее внешнее поле, тем больше
), причём, чем сильнее внешнее поле, тем больше 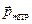 . И подобные магнитные моменты, направленные против поля, возникают у всех электронов в атоме, поэтому теперь намагниченность
. И подобные магнитные моменты, направленные против поля, возникают у всех электронов в атоме, поэтому теперь намагниченность  ~
~ 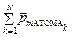 не только не равна нулю, но, так же, как и каждый из добавочных магнитных моментов, направлена в сторону, противоположную вектору
не только не равна нулю, но, так же, как и каждый из добавочных магнитных моментов, направлена в сторону, противоположную вектору  . Другими словами,
. Другими словами,  = c
= c  , но теперь c < 0.
, но теперь c < 0.
Эффект мал, ½c½ << 1 (обычно ½c½ » 10-6 - 10-5), и поэтому прецессия орбит, имеющая место и в случае парамагнетиков, на фоне уже имеющегося магнитного момента атома практически незаметна. Но в диамагнетиках, у которых в отсутствие внешнего магнитного поля суммарный магнитный момент атома равен нулю, именно возникновение прецессии под действием внешнего поля приводит к намагничиванию «против поля» и выталкиванию образца из этого поля.
Особенно явно эффект выталкивания наблюдается в случае сверхпроводников, которые являются идеальными диамагнетиками (у них c = - 1, то есть  = -
= -  , и магнитное поле внутри сверхпроводника полностью компенсируется: возникает «экранировка», подобная той, которая имеет место внутри уединённого проводника, помещённого в электростатическое поле). Природа столь сильного намагничивания против поля, однако, совсем иная. О том, что при этом происходит внутри сверхпроводника, мы поговорим при изучении третьей части курса физики.
, и магнитное поле внутри сверхпроводника полностью компенсируется: возникает «экранировка», подобная той, которая имеет место внутри уединённого проводника, помещённого в электростатическое поле). Природа столь сильного намагничивания против поля, однако, совсем иная. О том, что при этом происходит внутри сверхпроводника, мы поговорим при изучении третьей части курса физики.
 График зависимости J(H) для диамагнетика приведён на рис. 16.3: в отличие от рис 16.2 наклон прямой J(H) является заметно менее крутым, и при этом насыщения нет.
График зависимости J(H) для диамагнетика приведён на рис. 16.3: в отличие от рис 16.2 наклон прямой J(H) является заметно менее крутым, и при этом насыщения нет.
В твердом теле, помещённом в магнитное поле, свободные электроны начинают двигаться по замкнутым орбитам, создавая при этом добавочное магнитное поле, направленное противоположно внешнему. Эффект также невелик: диамагнетизм свободных носителей (диамагнетизм Ландау) по порядку величины сравним с диамагнетизмом электронных оболочек.
16.1.3 Ферромагнетизм. Петля гистерезиса
Особенностью ферромагнетиков является, во-первых, то, что явление намагничивания у них проявляется очень сильно (c >> 1) при этом магнитная восприимчивость этих веществ не является константой, а сама зависит от величины напряжённости магнитного поля, то есть c = c(H). Во-вторых, графики зависимостей J(H) и B(H) ферромагнетиков имеют вид петли: образцы, как бы «помнят» свою «предысторию» (как они намагничивались ранее); соответствующая петля носит название петли гистерезиса (от английского history, история).

Если ненамагниченный ферромагнетик поместить в магнитное поле, напряжённость которого можно увеличивать, график зависимости J(H) будет иметь вид, представленный на рис. 16.4.а). На начальном участке происходит быстрое возрастание намагниченности, но затем, после прохождения участка максимальной крутизны, рост J замедляется и кривая выходит на насыщение. Для достижения насыщения требуются поля гораздо меньшие, чем в случае парамагнетика.
Похожий вид имеет график зависимости B(H) с той только разницей, что он не выходит на насыщение, а всё более приближается к наклонной прямой линии (рис. 16.4.б). Это и понятно: согласно определению  =
= 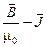 , или
, или  = m0(
= m0(  +
+  ), и, коль скоро J, выходя на насыщение, становится некоторой константой JS, то график зависимости B = m0(H + JS) оказывается прямой линией, отсекающей по оси ординат отрезок B = m0JS и имеющей тангенс угла наклона к оси абсцисс, равный m0.
), и, коль скоро J, выходя на насыщение, становится некоторой константой JS, то график зависимости B = m0(H + JS) оказывается прямой линией, отсекающей по оси ординат отрезок B = m0JS и имеющей тангенс угла наклона к оси абсцисс, равный m0.
На рис. 16.4.в) показан график зависимости от напряжённости магнитного поля для магнитной проницаемости вещества m. Так как  = m0(
= m0(  +
+  ) = m0(
) = m0(  + c
+ c  ) = m0(1 + c)
) = m0(1 + c)  = m0m
= m0m  , то это означает, что максимуму графика зависимости m(H) соответствует область с наибольшей крутизной прямой, проведённой из начала координат и являющейся при этом касательной к графику зависимости B(H).
, то это означает, что максимуму графика зависимости m(H) соответствует область с наибольшей крутизной прямой, проведённой из начала координат и являющейся при этом касательной к графику зависимости B(H).
Петля гистерезиса возникает, если по достижении насыщения (точка А на рис. 16.5.а) напряженность магнитного поля начать уменьшать. Окажется, что даже после того, как внешнее поле исчезнет, у образца сохранится остаточная намагниченность Jr, (точка B) для полного устранения которой необходимо поле c противоположным направлением вектора  . Значение напряжённости, при котором намагниченность вновь станет равной нулю, носит название коэрцитивной силы и обозначается HC (рис. 16.5.а, точка С). Очевидно, что коэрцитивная сила, как и напряжённость магнитного поля вообще, измеряется в амперах на метр.
. Значение напряжённости, при котором намагниченность вновь станет равной нулю, носит название коэрцитивной силы и обозначается HC (рис. 16.5.а, точка С). Очевидно, что коэрцитивная сила, как и напряжённость магнитного поля вообще, измеряется в амперах на метр.

Чем больше коэрцитивная сила, тем труднее перемагнитить образец. Вещества с большими значениями HC (то есть с широкой петлёй гистерезиса) называются магнитожёсткими, из них изготавливаются постоянные магниты; а вещества, характеризующиеся малой коэрцитивной силой (с узкой петлёй гистерезиса) – магнитомягкими. Из последних изготавливают сердечники для трансформаторов: в переменном электрическом поле, при котором работают эти устройства, происходит периодическое перемагничивание сердечников, и чем труднее это делать, тем большая доля электрической энергии вместо преобразования будет расходоваться на их перемагничивание.
Если после достижения нулевой намагниченности напряжённость магнитного поля продолжать увеличивать по величине, то намагниченность вновь выйдет на насыщение (точка D), при этом направление вектора  будет совпадать с направлением вектора
будет совпадать с направлением вектора  . Затем напряжённость магнитного поля можно начать уменьшать, и при H = 0 образец вновь станет иметь нулевую намагниченность (точка E). При H = HC намагниченность вновь окажется равной нулю (точка F) и в дальнейшем кривая зависимости вновь выйдет на насыщение: петля ABCDEFA замкнётся.
. Затем напряжённость магнитного поля можно начать уменьшать, и при H = 0 образец вновь станет иметь нулевую намагниченность (точка E). При H = HC намагниченность вновь окажется равной нулю (точка F) и в дальнейшем кривая зависимости вновь выйдет на насыщение: петля ABCDEFA замкнётся.
Аналогичная ситуация имеет место и в случае графика зависимости B(H), отличие заключается лишь в том, что концы петли оказываются не горизонтальными, а асимптотически стремятся к наклонной прямой, которой в области больших напряжённостей поля характеризует связь B и H (рис. 16.5.б).
При первом намагничивании J можно не доводить до насыщения, тогда петля гистерезиса окажется меньше по размерам. Подобные петли называются частными. Пример системы частных петель, лежащих внутри полной петли для зависимости B(H) представлен на рис. 16.5.в).
Магнитная восприимчивость c ферромагнетика и связанная с ней магнитная проницаемость m = 1 + c в сильной мере зависят от Н: они максимальны в области, где график зависимости J(Н) возрастает наиболее быстро. Кроме того, так же, как и у парамагнетиков, магнитная восприимчивость ферромагнетиков зависит от температуры. Эта зависимость приблизительно передается законом Кюри – Вейса:
c = 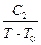 , (16.3)
, (16.3)
где TС - температура Кюри, по достижению которой ферромагнетик переходит в парамагнитное состояние; С2 - постоянная.
В отличие от диа- и парамагнетиков, магнитные свойства которых определяются поведением отдельных атомов или свободных электронов, характерной чертой ферромагнетиков является наличие в них областей самопроизвольного (спонтанного) намагничивания - доменов. Возникновение доменов в ферромагнетике обусловлено так называемым обменным взаимодействием электронов в атомах, которое имеет квантово-механическую природу. В результате этого взаимодействия собственные (спиновые) магнитные моменты электронов соседних атомов могут выстраиваться параллельно друг другу, и данный элемент объема вещества оказывается намагниченным до насыщения и приобретает отличный от нуля магнитный момент. Границы между доменами состоят из атомов, магнитные моменты которых образуют переходные области, постепенно меняя ориентацию от одного домена к другому. Характерные поперечные размеры доменов в железе, например, составляют 0,01 –0,1 мм, толщина доменных стенок (переходных областей) - около 0,0001 мм.
Ход кривой намагничивания ферромагнетика тесно связан с процессами, происходящими в доменах. Внутри каждого из них магнитные моменты электронов выстроены в одном направлении, однако магнитные моменты отдельных доменов имеют хаотическую ориентацию, при этом намагниченность магнетика равна нулю. Сказанное иллюстрируется рисунком 16.6, в верхней части которого изображены четыре домена, вектора намагниченности  которых имеют разные направления, поэтому при H = 0 сумма
которых имеют разные направления, поэтому при H = 0 сумма 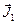 +
+ 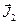 +
+  +
+  = 0. Внесём такой объект в магнитное поле, напряженность которого можно менять. В области малых полей нарастание Н ведет к росту размеров тех доменов, направление вектора
= 0. Внесём такой объект в магнитное поле, напряженность которого можно менять. В области малых полей нарастание Н ведет к росту размеров тех доменов, направление вектора  в которых составляет малые углы с вектором
в которых составляет малые углы с вектором  (на рис. 16.6.б)
(на рис. 16.6.б) 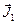 увеличивается до
увеличивается до 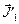 ,
,  увеличивается до
увеличивается до  , в то время, как
, в то время, как 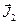 и
и  уменьшаются, соответственно, до
уменьшаются, соответственно, до  и
и  ). Увеличение размеров происходит путем перемещения границ доменов; в области малых полей процесс идет плавно, но затем (с ростом H) приобретает скачкообразный характер. При этом на кривой намагничивания появляются отдельные ступеньки (рис. 16.4.а); данное явление носит название эффекта Баркгаузена.
). Увеличение размеров происходит путем перемещения границ доменов; в области малых полей процесс идет плавно, но затем (с ростом H) приобретает скачкообразный характер. При этом на кривой намагничивания появляются отдельные ступеньки (рис. 16.4.а); данное явление носит название эффекта Баркгаузена.
 |
При дальнейшем увеличении напряжённости начинается разворот всех доменов по полю до тех пор, пока их магнитные моменты не станут параллельными вектору
 (на рис. 16.6.в) домены с
(на рис. 16.6.в) домены с  и
и  исчезли вовсе, а домены с
исчезли вовсе, а домены с 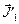 и
и  , ещё больше увеличившись в размерах и начав поворачиваться вдоль силовых линий приобрели магнитные моменты
, ещё больше увеличившись в размерах и начав поворачиваться вдоль силовых линий приобрели магнитные моменты 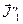 и
и  ). После полного разворота доменов по полю намагничивание закончится, а намагниченность выходит на насыщение (
). После полного разворота доменов по полю намагничивание закончится, а намагниченность выходит на насыщение (  и
и 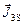 на рис. 16.6.г).
на рис. 16.6.г).
Если напряженность магнитного поля начать снижать, то перечисленные процессы пойдут в обратном направлении: сначала нарушится ориентация доменов, а затем начнут возникать домены, намагниченные под разными углами к вектору  . Границы новых доменов не совпадают с теми, которые были до намагничивания: разбиение на домены происходит «заново». Но даже при снижении напряжённости поля до нуля преимущественное направление у магнитных моментов доменов образца всё же сохранится. Возникает магнитный гистерезис: для размагничивания образца и полной разориентации доменов требуется создать поле HC, силовые линии которого имеют направление, противоположное первоначальному. Возможные варианты направления векторов намагниченности отдельных доменов на разных стадиях изменения H показаны стрелочками на рис. 16.6.д).
. Границы новых доменов не совпадают с теми, которые были до намагничивания: разбиение на домены происходит «заново». Но даже при снижении напряжённости поля до нуля преимущественное направление у магнитных моментов доменов образца всё же сохранится. Возникает магнитный гистерезис: для размагничивания образца и полной разориентации доменов требуется создать поле HC, силовые линии которого имеют направление, противоположное первоначальному. Возможные варианты направления векторов намагниченности отдельных доменов на разных стадиях изменения H показаны стрелочками на рис. 16.6.д).
Нагрев образца вносит хаос в ориентацию доменов. Если температура станет выше некоторого значения TС, энергия тепловых колебаний атомов превысит энергию обменного взаимодействия. В этом случае домены «распадутся»: магнитная связь между атомами нарушится, каждый из них будет реагировать на воздействие внешнего поля самостоятельно, и ферромагнетик превратится в парамагнетик. Температура такого перехода и называется точкой Кюри.
В заключение следует отметить, что существует важный класс кристаллов, которые можно представить в виде двух вставленных друг в друга подрешеток с противоположно направленными магнитными моментами атомов, причём эти моменты в сумме не компенсируют друг друга. Соответствующие вещества носят название ферритов. Ферриты ведут себя подобно ферромагнетикам, однако, замечательной особенностью, обусловившей их широкое применение, является высокое электрическое сопротивление таких материалов. Сопротивление ферритов превышает сопротивление металлов - ферромагнетиков в 105 – 1015 раз, что чрезвычайно важно при использовании этих материалов в диапазоне сверхвысоких частот (в СВЧ-диапазоне). В обычных ферромагнетиках на этих частотах возникают вихревые токи Фуко, которые резко снижают к. п. д. соответствующих устройств, разогревая их и выводя из строя. Ферритовые же сердечники, благодаря своему большому сопротивлению позволяют резко снизить тепловые потери: вихревые токи в них оказываются во много раз меньше. Общая химическая формула многих ферритов может быть записана в виде MeO×Fe2O3, где символ Me означает двухвалентный металл: Mg, Ni, Co, Cu и др.
Ферриты широко применяются при изготовлении магнитной ленты и дисков для аудио- и видеозаписывающих систем, элементов запоминающих устройств современных компьютеров. Присваивая положительному значению остаточной намагниченности Jr отдельного участка ленты или диска значение «1», а отрицательному – значение «0», на подобном носителе с помощью внешнего магнитного поля можно записывать и хранить информацию в двоичном коде.
Некоторые примеры
- Наличие у электронов собственного (спинового) момента импульса и связанного с ним магнитного момента объясняется в рамках релятивисткой квантовой механики. Таким образом, используя в повседневной жизни постоянные магниты, мы каждый раз сталкиваемся с объектами, понять природу которых можно, лишь зная квантовую механику и специальную теорию относительности.
- Управляя движением порошков, приготовленных на основе ферромагнитных частиц, можно шлифовать и полировать поверхности изделий, дробить мелкие объекты, смешивать сыпучие и жидкие материалы, перемещать введённые в их потоки объекты.
- Магнитное поле влияет на размеры ферромагнитного образца (например, на длину ферромагнитного стержня), поскольку при намагничивании происходит некоторое изменение расстояния между атомами. Образец может как расширяться, так и сжиматься – этот эффект используется для получения ультразвука.
- Долгое время считалось, что в кристаллической решетке ферромагнетика обязательно должны присутствовать атомы группы железа или редкоземельные элементы. В настоящее время, однако, уже синтезированы кристаллы на основе органических соединений, правда, их ферромагнитные свойства проявляются лишь при температуре ниже 1,5 К.
- Если ферромагнетик размельчить до частиц, имеющих размеры порядка одного домена (реально – несколько микрометров), а затем размешать полученный порошок в жидкости (воде, керосине, минеральном или силиконовом масле), получится магнитная жидкость, движением которой можно управлять, используя магнитное поле. Магнитным полем можно менять плотность и вязкость (вплоть до «затвердевания») такой жидкости, её оптическую прозрачность.
Вопросы для повторения
1. Объясните, чем обусловлено явление парамагнетизма.
2. Объясните, чем обусловлено явление диамагнетизма.
3. Что такое «домены» и какую роль они играют в формировании свойств ферромагнетика?
4. Начертите графики зависимости намагниченности от напряжённости магнитного поля для пара- и диамагнетиков. Чем отличаются эти графики?
5. Объясните, что называется петлёй гистерезиса, и какие физические процессы приводят к её возникновению.
6. Что называется остаточной индукцией, остаточной намагниченностью, коэрцитивной силой, и в каких единицах эти параметры измеряются в СИ?
7. Как изменение температуры влияет на магнитные свойства материалов?
Дата добавления: 2020-02-05; просмотров: 625;











