Лекция 12 ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК. ЧАСТЬ II

12.1 ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ (продолжение)

12.1.1 Соединение элементов цепи постоянного тока. Правила Кирхгофа

12.1.2 Закон Джоуля-Ленца

12.1.3 Достоинства и недостатки классической теории электропроводности

12.2 ЭЛЕКТРИЧЕСКИЙ ТОК В ВАКУУМЕ, ЖИДКОСТЯХ И ГАЗАХ

12.2.1 Явление термоэлектронной эмиссии. Вакуумный диод

12.2.2 Электрический ток в жидкостях. Явление электролиза

12.2.3 Электрический ток в газах. Виды газового разряда

Некоторые примеры

Вопросы для повторения

12.1 ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ (продолжение)

12.1.1 Соединение элементов цепи постоянного тока. Правила Кирхгофа

Два элемента цепи (резистора, конденсатора, источника э. д. с. и др.) можно соединить друг с другом или последовательно, или параллельно. Если на участке цепи элементов больше, чем два, их общее соединение может оказаться более сложным, но вполне вероятно, что хотя бы часть из элементов (или их комбинаций) соединена друг с другом каким-либо их этих способов. Расчёт значений падения напряжения на отдельных элементах электрических цепей, токов идущих через эти элементы (или зарядов на конденсаторах) в случае данных двух типов соединений достаточно прост, поэтому их нужно уметь выявлять, то есть знать определения, какое соединение является последовательным, а какое – параллельным. При этом следует помнить, что на электрических схемах точки, имеющие одинаковый потенциал, соединяются тонкой линией, вдоль которой значение потенциала, естественно, также не меняется.

Последовательное соединение

При последовательном соединении двух элементов цепи потенциал на одном из выводов первого элемента равен потенциалу на одном из выводов второго элемента, причём к участку цепи с этим потенциалом не подключено больше никаких других элементов цепи.

Рассмотрим несколько примеров.

На рис. 12.1.а) пластина Б конденсатора C₁ соединена с пластиной В конденсатора C₂; в точке соединения (на участке БВ) никаких других подключений нет: конденсаторы соединены последовательно.

Аналогичная схема изображена на рис 12.1.б): вывод Б резистора R₁ соединён в выводом В резистора R₂, и в точке их соединения (на участке БВ) других подключений не имеется.

На схеме, изображённой на рис. 12.1.в), последовательно соединённых резисторов нет вовсе: так, например, хотя вывод В резистора R₁ и соединён с выводом Г резистора R₂, но в точке их соединения (на участке ВГ) есть добавочное подключение (резистора R₃). По той же причине не является последовательным соединение резисторов R₄ и R₅[9].

Параллельное соединение

При параллельном соединении двух элементов цепи потенциалы на их выводах попарно равны.

На рис. 12.2.а) конденсаторы C₁ и C₂ соединены параллельно, так как потенциалы на их выводах попарно равны (на Б и Д потенциал j₁, на В и E – потенциал j₃.

На схеме 12.2.б) вывод В резистора R₁ имеет тот же потенциал (j₁), что и вывод Г резистора R₂, а вывод Б резистора R₁ – тот же потенциал (j₂), что и вывод Д резистора R₂, следовательно, резисторы соединены параллельно.

Нетрудно убедиться в том, что в общем случае (когда j₂ = j*₂) нет параллельно соединённых резисторов и на рис. 12.1.в).

Совокупность двух последовательно или параллельно соединённых резисторов (конденсаторов, источников э. д. с. и т. д.) можно представить в виде одного элемента цепи, параметры которого можно рассчитать, используя соответствующие определения.

Пример 1. Последовательное соединение конденсаторов

Участок АБ, объединяющий правую пластину конденсатора С₁, левую пластину конденсатора C₂ и соединяющий их провод АБ (рис. 12.3) можно считать отдельным проводником, никак не соединённым с другими элементами цепи. Это означает, что если изначально он был электронейтральным, то после того, как на пластине А накопится заряд -q, компенсирующий заряд +q на левой пластине этого же конденсатора, на другом конце проводника (на пластине Б второго конденсатора) останется заряд также +q: в целом участок АБ останется электронейтральным (по закону сохранения электрического заряда). С учётом этого, а также использовав обозначения U₁ = j₁ - j₂, U₂ = j₂ - j₃, U_ПС = j₁ - j₃ и определение электроёмкости конденсатора (C = q/U), можно записать:

q_ПС = q₁ = q₂ = q,

U_ПС = j₁ - j₃ = (j₁ - j₂) + (j₂ - j₃) = U₁ + U₂,

= = = + = + .

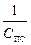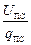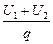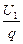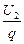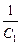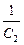Итак, при последовательном соединении конденсаторов

q_ПС = q₁ = q₂, U_ПС = U₁ + U₂, 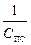= 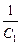+ 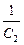. (12.1)

Пример 2. Последовательное соединение резисторов (рис. 12.4).

По закону сохранения электрического заряда, какой заряд войдёт в каждый из резисторов, такой же из него и выйдет, то есть токи I₁ и I₂ должны быть одинаковыми (I₁ = I₂ = I). С учётом того, что U₁ = j₁ - j₂, U₂ = j₂ - j₃, U_ПС = j₁ - j₃, а также использовав определение электрического сопротивления (согласно которому R = U/I), запишем:

I_ПС = I₁ = I₂ = I,

U_ПС = j₁ - j₃ = (j₁ - j₂) + (j₂ - j₃) = U₁ + U₂,

R_ПС = U_ПС/I_ПС = (U₁ + U₂)/I = U₁/I + U₂/I = R₁ + R₂.

В итоге при последовательном соединении резисторов:

I_ПС = I₁ = I₂, U_ПС = U₁ + U₂, R_ПС = R₁ + R₂. (12.2)

Пример 3. Параллельное соединение конденсаторов (рис. 12.5).

Поскольку весь участок БАД является единым проводником (состоящим из двух пластин Б и Д и соединяющего их провода), общий заряд этого участка равен сумме зарядов q₁ и q₂. Следовательно,

q_ПР = q₁ + q₂

U_ПР = j₁ - j₃ = U₁ = U₂ = U

C_ПР = q_ПР/U_ПР = (q₁ + q₂)/U = q₁/U + q₂/U = C₁ + C₂.

Таким образом, при параллельном соединении конденсаторов

q_ПР = q₁ + q₂, U_ПР = U₁ = U₂, C_ПР = C₁ + C₂. (12.3)

Пример 4. То, что при параллельном соединении резисторов

I_ПР = I₁ + I₂, U_ПР = U₁ + U₂, 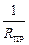= 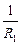+ 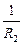, (12.4)

студентам предлагается убедиться самостоятельно.

В общем случае для расчёта значений напряжения и силы тока на отдельных участках цепи можно использовать правила Кирхгофа, которые применимы не только в цепях постоянного, но и в цепях переменного токов.

Согласно первому правилу Кирхгофа алгебраическая сумма токов в узле электрической цепи равна нулю:

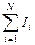= 0. (12.5)

Слова «алгебраическая сумма» означают, что значения тех токов I_i, которые входят в узел, в формуле (12.5) нужно брать с одним знаком, тех, которые выходят из узла, – с противоположным. Так, например, для узла Б на рис. 12.6: I₃ - I₁ + I₂ + I¢ = 0, для узла Ж, соответственно, I₁ - I₃ - I₅ = 0, и т. д.

Нетрудно заметить, что в основе первого правила Кирхгофа лежит закон сохранения электрического заряда.

Второе правило Кирхгофа относится к замкнутым участкам электрической схемы (на рис. 12.6 это, например, участки БВГДБ, АБДЕЖИА и др.). Выбирая направление обхода каждого такого участка (например, по часовой стрелке) и учитывая те токи, которые совпадают с направлением обхода, как положительные, а противоположные им, как отрицательные, можно записать выражение, отражающее суть закона.

Второе правило Кирхгофа: сумма падений напряжения на элементах замкнутого участка цепи равна алгебраической сумме э. д. с. на этом участке:

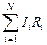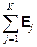= . (12.6)

Фраза «алгебраическая сумма э. д. с.» означает, что э. д. с. тех источников, которые включены так, чтобы помогать прохождению тока в направлении обхода, при суммировании нужно брать со знаком «плюс», а тех, которые мешают – со знаком «минус».

В частности, для участка БВГДБ формула записывается так:

-I¢r₁ + I₂R₂ = - E₁.

Для участка АБДЕЖИА

-I₁R₁ - I₂R₂ - I₅r₃ - I₅R₅ - I₁R₄ - I₁r₂ = E₃ - E₂.

Нетрудно заметить, что если цепь сама по себе представляет собой лишь один замкнутый контур, второе правило Кирхгофа превращается в формулировку закона Ома для замкнутой (полной) цепи.

Подробнее правила Кирхгофа и приёмы работы с ними рассматриваются в курсе «Теоретические основы электротехники».

12.1.2 Закон Джоуля-Ленца

Как мы уже говорили ранее, перемещая заряды, силы электрического поля совершают работу A = q(j₁ - j₂). Если перемещение заряда означает протекание по проводнику постоянного электрического тока, то, по определению силы тока, q = IDt, где Dt – время, за которое совершается работа.

Совершение работы сопровождается изменением энергии проводника (его нагревом, протеканием химических реакций в электролите). Если вся работа идёт только на нагрев однородного участка цепи (преобразуется в тепловую, внутреннюю энергию резистора), то для выделяющегося количества теплоты Q можно записать, что Q = I(j₁ - j₂)Dt, а с учётом закона Ома для такого участка:

Q = I²RDt. (12.7)

Данное соотношение носит название закона Джоуля-Ленца.

Если ток – не постоянный, то эту же формулу можно записать для малого промежутка времени dt:

dQ = I²Rdt. (12.8)

Тогда тепло, выделившееся за время t, рассчитывается, как

Q = 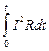. (12.9)

С учётом того, что I = jS, где j – плотность тока, S – площадь поперечного сечения проводника (для простоты будем считать проводник однородным цилиндром c удельным сопротивлением r и длиной l, для которого R = rl/S)

dQ = (jS)²r 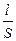dt = j²rSldt . (12.10)

Произведение Sl – объём проводника V, поэтому 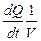= j²r. Последнее выражение (количество теплоты, выделяющейся в единице объёма в единицу времени) называют удельной тепловой мощностью тока Q_УД, а формулу

Q_УД = j²r (12.11)

– законом Джоуля-Ленца, записанным в дифференциальной форме.

12.1.3 Достоинства и недостатки классической теории

электропроводности

То, что, пользуясь представлениями классической теории электропроводности, рассматривающей совокупность электронов в металле как газ свободных электронов, ускоряемых электрическим полем, нам удалось вывести основные законы постоянного тока, которые подтверждаются экспериментом, является несомненным достоинством теории. Если бы теории была неверна, вряд ли можно было бы рассчитывать работу электрических схем, конструировать электрические приборы, комплексы и системы. Становление современной цивилизации невозможно представить без использования электричества, и роль классической теории в этом процессе трудно переоценить. Тем не менее, уже в начале ХХ века накопился комплекс проблем, вопросов, на которые эта теория ответа дать не могла. Среди таких вопросов (и в этом –недостаток классической теории) отметим следующие три:

· Как мы отметили на прошлой лекции, согласно классической теории температурная зависимость удельного сопротивления должна иметь вид:

r = 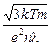, или r ~ .

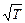На практике, однако, в диапазоне температур, близких к комнатным, для многих металлов данная зависимость линейна (то есть r ~ T). С чем это может быть связано, классическая теория ответа не даёт.

· При низких (близких к 0 К) температурах отличие теории от данных эксперимента становится особенно явным: многие металлы при температуре, меньшей некоторого значения (зависящего от природы металла и ряда других условий) переходят в сверхпроводящее состояние. Их сопротивление становится не просто малым, оно исчезает вовсе, наблюдается явление сверхпроводимости. Данное явление классическая теория объяснить не в состоянии.

· Существует класс материалов, которые во многом ведут себя как металлы: плавятся при нагреве, обладают характерным металлическим блеском, пластичны, проводят электрический ток и т.д. Однако, если повышение температуры обычного металла сопровождается увеличением его сопротивления, то у таких материалов рост T приводит к уменьшению r. Эти материалы называются полупроводниками, какова природа процессов, которые объясняют подобное поведение подобных объектов, классическая теория описать также не может.

Ответы на эти и ряд других вопросов физикам удалось дать только после создания квантовой теории, с основными положениями которой мы познакомимся позднее.

12.2 ЭЛЕКТРИЧЕСКИЙ ТОК В ВАКУУМЕ, В ЖИДКОСТЯХ

И В ГАЗАХ

12.2.1 Явление термоэлектронной эмиссии. Вакуумный диод

Термоэлектронной эмиссией называется явление испускания электронов нагретыми металлами.

Электронный газ в металле характеризуется средней кинетической энергией хаотического (теплового) движения отдельных электронов. Однако при комнатной температуре этой энергии недостаточно для совершения работы против сил притяжения со стороны ионов кристаллической решётки, поэтому электроны не могут вырваться из металла. Нагрев приводит к повышению средней кинетической энергии электронов, при этом часть из них становится способна преодолеть силы притяжения со стороны ионов решетки и вылететь из металла.

Явление термоэлектронной эмиссии лежит в основе работы вакуумных электронных ламп, простейшей из которых является вакуумный диод.

При нагреве катода (отрицательного электрода, см. рис. 12.7.а) электроны начинают вылетать из него; если же между катодом и анодом (положительный электрод) существует электрические поле, часть электронов устремляется к аноду, а часть всё же возвращается на катод. При увеличении анодного напряжения U ток через диод возрастает до тех пор, пока все вылетающие из катода электроны не станут достигать анода; после этого вольтамперная характеристика диода (рис. 12.7.б) выйдет на насыщение.

Увеличить ток насыщения можно, повысив температуру накала катода. Температура возрастает – увеличивается число электронов, способных вылететь из катода – ток насыщения становится больше. Зависимость плотности тока насыщения вакуумного диода от температуры катода описывается формулой Ричардсона-Дэшмена:

j = BT² 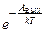. (12.12)

В этой формуле A_ВЫХ – работа выхода (минимальная работа, которую должен совершить электрон с тем, чтобы преодолеть силы притяжения со стороны ионов кристаллической решётки и вылететь из металла). Величина A_ВЫХ зависит, прежде всего, от природы металла и от наличия в нём примесей, её значение можно найти в соответствующих таблицах. Коэффициент B отражает зависимость плотности тока насыщения от особенностей конструкции лампы, размеров и формы электродов.

Нетрудно заметить, что вакуумный диод – пример элемента электрической цепи, не подчиняющийся закону Ома: его вольтамперная характеристика нелинейна (если бы для диода закон Ома, согласно которому I ~ U выполнялся, то график вольтамперной характеристики имел бы вид, изображённый на рис. 12.7.б пунктиром). Во-первых, в отличие от резистора, диод пропускает ток лишь в одном направлении (когда катод имеет отрицательный потенциал). Это свойство диода используется в радиотехнике для выделения из переменных сигналов компонент лишь одной полярности. Во-вторых, ток через диод с ростом U выходит на насыщение, чего также нельзя сказать о токе через резистор. Даже при малых значениях напряжения между анодом и катодом рост силы тока происходит быстрее, чем в законе Ома. На начальном участке вольтамперной характеристики диода выполняется «закон трёх вторых», согласно которому при не слишком больших U

I ~ 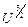. (12.13)

Более подробно с работой простейших вакуумных ламп (диода и триода) многие из вас ознакомятся при выполнении лабораторного практикума.

12.2.2 Электрический ток в жидкостях. Явление электролиза

Для того, чтобы жидкость проводила электрический ток, она должна содержать переносчики электрического заряда, в качестве которых чаще всего выступают положительно и отрицательно заряженные ионы самой жидкости или веществ, растворённых в ней. При растворении в воде, например, соли хлорного железа (FeCl₃) под влиянием электрического поля, создаваемого ионами Н⁺ и ОН^-, происходит электролитическая диссоциация – разрушение молекулы хлорида железа и образования ионов Fe⁺³ и Cl^-:

FeCl₃ « Fe⁺³ + 3Cl^-.

Если в такой раствор погрузить два электрода и создать на них разность потенциалов, то через электролит пойдёт ток: ионы Fe⁺ начнут двигаться к катоду, а ионы Cl^- – к аноду (рис. 12.8). Достигнув электродов, ионы захватывают заряд противоположного знака и превращаются в нейтральные атомы. Это означает, что катод начнёт покрываться слоем железа, а вблизи анода станет выделяться хлор.

Вещества, растворы которых хорошо проводят электрический ток, называются электролитами. Таким образом, прохождение электрического тока через электролит тесно связано с переносом вещества – ионов растворённого соединения.

М. Фарадей установил два закона электролиза:

Первый закон:

Масса вещества m, выделившегося на электроде, прямо пропорциональна заряду Dq, прошедшему через электролит:

m = kDq, (12.14)

где k – электрохимический эквивалент вещества (постоянная для данного вещества величина).

Второй закон:

Электрохимический эквивалент вещества пропорционален его атомной массе M_A и обратно пропорционален валентности nдвижущихся ионов:

k = 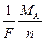, (12.15)

где F =965000 Кл/моль – постоянная Фарадея.

Можно легко показать, что F = eN_A, где е – заряд электрона, N_A – число Авогадро.

12.2.3 Электрический ток в газах

В обычных условиях газы не проводят электрический ток, то есть являются диэлектриками. Внешние воздействия, однако, могут способствовать появлению в газе свободных носителей заряда: электронов и положительно заряженных ионов, и тогда газ начнёт проводить электрический ток.

Если носители заряда возникают в газе в результате внешних воздействий, не связанных с электрическим полем (освещением, нагревом, радиоактивным излучением), то обусловленная этими носителями проводимость называется несамостоятельной. Если носители тока возникают вследствие воздействия на газ сил электрического поля, проводимость называется самостоятельной.