Лекция 13 МАГНИТНОЕ ПОЛЕ. ЧАСТЬ I

13.1 ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ

13.1.1 Магнитное поле. Силовые линии. Сила Ампера. Вектор магнитной индукции

13.1.2 Взаимодействие параллельных токов. Ампер – основная единица СИ

13.1.3 Закон Био-Савара-Лапласа

Некоторые примеры

Вопросы для повторения

13.1 ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ

13.1.1 Магнитное поле. Силовые линии. Сила Ампера.

Вектор магнитной индукции

С древних времён известно, что существуют вещества, обладающие магнитными свойствами, из которых можно изготавливать постоянные магниты. У таких магнитов два полюса, причём один из полюсов стремится повернуться на север (его так и называют – северным полюсом магнита), другой – к югу (южный полюс магнита). Одноименные полюса двух магнитов отталкиваются, разноименные – притягиваются.

Поскольку магниты ориентируются в пространстве относительно Земли определённым образом, естественно предположить, что и сама Земля является большим постоянным магнитом (рис. 13.1). На севере находится её южный магнитный полюс (территориально он расположен в западном полушарии в Северном ледовитом океане), а на юге (в Антарктиде) – северный магнитный полюс (в этой точке, известной так же, как полюс холода, находится Российская станция «Восток»). К слову сказать, магнитные поля есть не у всех планет, нет магнитного поля и у спутника Земли – Луны. Положение магнитных полюсов у небесных объектов также не является постоянным, так, например, каждые 11 лет происходит смена полюсов на Солнце; на Земле за время её существования изменение положения магнитных полюсов происходило, по меньшей мере, три раза, да и в настоящее время магнитные полюса нашей планеты медленно, но движутся.

Северный полюс постоянных магнитов принято обозначать буквой N и окрашивать в синий цвет, южный – буквой S и окрашивать в красный цвет.

В 1827 году Эрстед открыл, что магнитным полем обладают не только постоянные магниты: оно возникает вокруг любых проводников, по которым идёт электрический ток. Другими словами, магнитное поле оказалось связано с направленным движением зарядов, и этот факт лёг в основу классической теории магнетизма, которая изначально создавалась по аналогии с классической теорией электричества. Существенная разница этих двух теорий заключается в том, что, в отличие от двух типов зарядов (положительных и отрицательных), по отдельности «северных» и «южных» полюсов («магнитных зарядов») обнаружить не удаётся. Если магнит разделить на две части, то у каждой из них будут свои северный и южный полюса; и хотя есть теоретические модели, в которых делаются предположения о существовании в природе объектов с «магнитным зарядом» лишь одного «знака» (они носят название «монополей Дирака»), эксперимент пока не может подтвердить их справедливость.

Слова «магнитное поле» означают, что в каждой точке пространства на полюса помещаемого в эту точку маленького магнита будут действовать определенные силы, стремящиеся развернуть этот магнит. В связи с этим для графического отображения магнитного поля, принято использовать силовые линии (подобно тому, как это делается в случае электрического поля). В данном случае силовой называется линия, касательная в каждой точке к которой совпадает по направлению с силой, действующей на северный полюс маленького магнита, помещаемого в эту точку. Из определения следует, что силовые линии должны выходить из северного полюса магнита и входить в южный. Примерный вид силовых линий магнитных полей, создаваемых разными объектами, изображён на рис. 13.2: а) поле постоянного магнита; б) поле соленоида с током; в) поле кругового витка с током; г) поле прямого проводника с током. Из рисунка следует, что магнитное поле маленького постоянного магнита эквивалентно полю одного витка с током.

Поскольку термин «поле» неразрывно связан со словом «сила», обсудим, какая сила действует в магнитном поле на объект, обладающий магнитными свойствами, и прежде всего – на прямой участок проводника с током.

Пусть в поле, создаваемое постоянным магнитом, помещён проводник с током (рис. 13.3). Выделим на проводнике малый прямой участок длиной dl: в магнитном поле на этот участок действует сила dF, величина которой зависит от силы тока в проводнике I, от длины участка dl, а также от угла a между направлением протекания тока и направлением силовых линий поля в месте, где находится рассматриваемый участок.

Очевидно, эффект зависит и от того, насколько «велико» само поле, то есть в итоговую формулу для расчёта dF должна входить некая силовая характеристика поля. Эта характеристика носит название вектора магнитной индукции , который по направлению совпадает с силой, действующий на северный полюс маленького магнита. Таким образом,

dF = IBsina×dl. (13.1)

Данная формула позволяет характеризовать магнитное поле количественно. Действительно, поместив в заданную точку пространства прямой проводник заданной длины, и пропустив по нему известный ток, можно измерить действующую на проводник силу, после чего – вычислить значение магнитной индукции:

B = 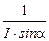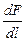. (13.2)

В СИ индукция магнитного поля измеряется в теслах (Тл).

Если участку проводника сопоставить вектор , по величине, равный длине dl этого участка, и направленный в ту сторону, в которую идёт ток, то, с учётом того, что индукция магнитного поля также является вектором, выражение (13.1) можно переписать в виде

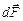= I[ ]. (13.3)

Сила, рассчитываемая по этой формуле, носит название силы Ампера, её величина описывается выражением (13.1), а направление определяется так же, как это делается всегда в случае векторного произведения (например, по правилу буравчика или по правилу левой руки: пальцы руки направляются по первому вектору-сомножителю, второй вектор-сомножитель должен «входить в ладонь», и тогда отставленный в сторону большой палец покажет направление векторного произведения).

Если проводник – прямой и весь находится в однородном магнитном поле, то сила Ампера рассчитывается по формуле:

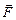= I[ ], (13.4)

где – вектор, по величине, равный длине l проводника, и направленный в ту же сторону, в которую идёт ток.

13.1.2 Взаимодействие параллельных токов.

Ампер – основная единица СИ

Поскольку вокруг любого проводника с током имеется магнитное поле, это означает, что два проводника, по которым идут токи, должны взаимодействовать друг с другом. В качестве примера рассмотрим два прямых, бесконечно длинных тонких проводника, расположенных параллельно друг другу. Каждый их них создаёт вокруг себя магнитное поле, которое действует на «соседа», силы взаимодействия, естественно, равны по величине и противоположны по направлению (третий закон Ньютона). Определим, в каком направлении будут действовать эти силы.

Пусть токи в проводниках идут в одну сторону (рис. 13.4). Проводник с током I₁ находится в поле, создаваемом вторым проводником (его индукция в том месте, где находится первый проводник, равна , вектор направлен от нас). Следовательно, на первый проводник со стороны второго действует сила , которая, в соответствии с правилом левой руки, направлена направо. Аналогично, проводник с током I₂ находится в поле первого проводника, вектор магнитной индукции которого направлен на нас. Сила 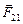, действующая на второй проводник со стороны первого, направлена налево. Таким образом, проводники, по которым токи идут в одном направлении, притягиваются.

Что произойдёт с проводниками, по которым токи идут в противоположных направлениях, студентам предлагается определить самостоятельно.

Взаимодействие прямых параллельных проводников с током положено в основу эталона ампера – основной единицы СИ. По определению, 1 А, это такая сила постоянного тока, который при прохождении по двум прямолинейным параллельным проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенным в вакууме на расстоянии 1 м друг от друга, вызывал бы на каждом участке проводника длиной 1 м силу взаимодействия, равную 2×10^-7 Н.

13.1.3 Закон Био-Савара-Лапласа

Для вычисления силы, которая будет действовать на один проводник со стороны другого, необходимо уметь рассчитывать индукцию магнитного поля, создаваемого проводником с током на заданном расстоянии от него (в том числе – в случае, если второй проводник не является прямым). Вычислить индукцию магнитного поля 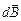, создаваемого малым участком проводника, по которому идёт ток I, в точке, положение которой задаётся радиус-вектором 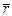(см. рис. 13.5), можно, пользуясь законом Био-Савара-Лапласа, который в СИ имеет вид:

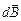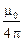
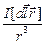= . (13.5)

В этой формуле m₀ = 4p×10^-7 Гн×м^-1 – магнитная постоянная (о единице измерения индуктивности – генри – мы поговорим позднее).

По величине dB = = ,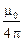

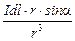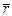где a угол между векторами и ; согласно правилу левой руки (или правилу буравчика), применённому для векторного произведения 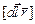, вектор 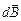направлен вглубь рисунка («от нас»).

Для нахождения общей индукции магнитного поля, создаваемого всем проводником в целом, следует применить принцип суперпозиции, согласно которому индукция магнитного поля, создаваемого системой разных объектов (проводников с током, постоянных магнитов), равна векторной сумме векторов индукции магнитных полей, создаваемых каждым объектом в отдельности:

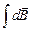= . (13.6)

В виде примера рассмотрим, как используется закон Био-Савара-Лапласа для расчёта индукции магнитного поля, создаваемого в центре кругового витка с током.

Пусть по круговому витку радиусом R идёт ток I (рис. 13.6.а). Выделим на витке малый участок (направление этого вектора совпадает с направлением протекания тока) и запишем, чему равна индукция магнитного поля, создаваемого этим участком в центра витка. Учитывая, что радиус окружности всегда перпендикулярен любому малому участку этой окружности (a = 90º), запишем:

dB = 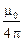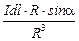= 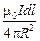. (13.7)

По правилу левой руки вектор 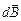на рисунке направлен вверх, причём это направление одинаково для всех малых элементов , выбираемых на окружности. Это означает, что и результирующий вектор в центре окружности будет направлен вверх, то есть, интегрировать можно уже не сами вектора 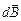, а их проекции на вертикальную ось, скаляры dB – см. (13.7):

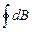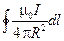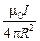
B = = = = 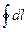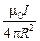×2pR = .

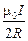Таким образом, индукция магнитного поля в центре кругового витка с током рассчитывается по формуле

B = 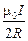. (13.8)

Используя закон Био-Савара-Лапласа, можно вывести формулы для индукции магнитного поля, создаваемого:

· на оси кругового витка с током на высоте h над плоскостью витка (рис. 13.6.б):

B = 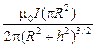. (13.9)

· на расстоянии r₀ от прямого отрезка проводника с током, концы которого из точки наблюдения видны под углами a₁ и a₂ (рис. 13.6.в):

B = 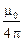(cosa₁ - cosa₂). (13.10)

В частности, для бесконечно длинного проводника a₁ ® 0º, a₂ ® 180º, и выражение (13.10) принимает вид:

B = . (13.11)

· внутри соленоида, имеющего n витков на единицу длины, на его оси в точке, из которой края соленоида видны под углами a₁ и a₂ (рис. 13.6.г):

B = m₀nI(cosa₂ - cosa₁). (13.12)

Для бесконечно длинного соленоида a₁ ® 180º, a₂ ® 0º, и для индукции магнитного поля внутри соленоида можно записать:

B = m₀nI. (13.13)

Формулы (13.11) и (13.13) мы выведем позднее, используя теорему о циркуляции вектора индукции магнитного поля.

Некоторые примеры

- Индукция магнитных полей, возникающих при функционировании человеческого мозга, составляет около 10^-9 Тл.

- Индукция магнитного поля, создаваемого магнитными аппликаторами, которые используются в медицине для снижения мышечных болей, составляет около 10 мТл.

- Крупные электромагниты с железными сердечниками создают в промежутке между полюсами магнитную индукцию до 6 Тл; на уникальных установках, созданных в СССР и США, удавалось достичь индукции до 50 Тл.

- Магнитное поле нейтронных звёзд может превышать 10¹⁰ Тл, при этом энергия взаимодействия электрона с магнитным полем оказывается соизмеримой с его энергии покоя m_ec², что должно приводить к появлению специфических релятивистских эффектов.

Вопросы для повторения

1. Сформулируйте закон Ампера и приведите пример его проявления.

2. Дайте определение вектору индукции магнитного поля. В каких единицах магнитная индукция измеряется в СИ?

3. Как графически отображается магнитное поле? Приведите примеры.

4. Объясните, как взаимодействуют бесконечно длинные параллельные проводники, по которым токи идут: а) в одном направлении; б) в противоположных направлениях.

5. Дайте определение основной единице СИ – амперу.

6. В чём заключается закон Био-Савара-Лапласа? Приведите пример его применения.