Расчет главной балки при усложненном типе балочной клетки
Главная балка проектируется составного сварного симметричного двутаврового сечения.
Определение нормативных и расчетных нагрузок
При действии на балку более 4-х сосредоточенных сил, нагрузка принимается равномерно распределенной. Выделим две составляющие этой нагрузки:
- составляющая, вызванная действием временной нагрузки
q нвр = b pн (6.1)
q вр = b pн g f v (6.2)
- составляющая, вызванная действием постоянной нагрузки (собственный вес конструкций)
q нпост = b( gнн + gнбн + gнвб ) (6.3)
qпост = b[ gнн gfg + a( gнбн + gнвб )] (6.4)
где b - шаг главных балок (м), принимается по заданию на проектирование, a =1,02– 1,05 – коэффициент, учитывающий собственную массу балки.
gнбн = gсвбн / a,
где gнбн - нормативная нагрузка от собственного веса балок настила, кН/м2;
gсвбн -линейная плотность балок настила по сортаменту, кг/п.м.
gнвб = gсввб / b1 - нормативная нагрузка от собственного веса балок настила и вспомогательных балок (кН/м2)
gнвб - нормативная нагрузка от собственного веса вспомогательных балок, определяется аналогично нагрузке от балок настила, кН/м2.
В том случае если количество сосредоточенных сил, действующих на главную балку, меньше или равно четырем, нагрузками будут являться опорные реакции балок настила (при нормальном типе балочной клетки), либо опорные реакции вспомогательных балок (при усложненном типе балочной клетки).
Определение усилий
Усилия, действующие в характерных сечениях главной балки и необходимые для дальнейших расчетов, определяются в зависимости от принятой расчетной схемы.
В однопролетной разрезной балке при действии равномерно-распределенной нагрузки максимальный изгибающий момент, действующий в середине пролета
M = (q вр + qпост ) L2/8 (6.5)
Mн = (qнвр + qнпост ) L2/8 (6.6)
Максимальная величина поперечной силы (она же – опорная реакция)
Q = (q вр + qпост ) L /2 (6.7)
В двухконсольной балке при действии равномерно-распределенной нагрузки максимальный пролетный изгибающий момент
Mпр = (q вр + qпост ) Lпр 2/8 - qпост Lк 2/2 (6.8)
Mнпр = (qнвр + qнпост ) Lпр 2/8 – qнпост Lк 2/2 (6.9)
- максимальный опорный момент
Mк = (q вр + qпост ) Lк 2/2 (6.10)
Поперечная сила, действующая в опорном сечении со стороны консоли
Qк = (q вр + qпост ) Lк /2 (6.11)
- в опорном сечении со стороны пролета
Qпр =(q вр + qпост ) Lпр /2 (6.12)
Максимальная величина опорной реакции двухконсольной балки
Rmax=(q вр + qпост ) ( Lпр /2 + Lк) (6.13)
При действии на главную балку сосредоточенных нагрузок усилия в ней определяются по правилам сопротивления материалов.
Компоновка сечения
Компоновка сечения, то есть определение размеров элементов в пределах принятого типа сечения (рис.5), является технико-экономической задачей: необходимо выбрать размеры элементов сечения из предлагаемого перечня (сортамента) таким образом, чтобы удовлетворялись условия прочности, жесткости, общей и местной устойчивости, конструктивные требования и, в то же время, принятое сечение имело минимальный вес.
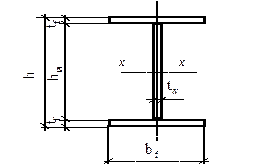
Рис. 5. Составное сечение главной балки
Из определяемых параметров сечения (hw, tw, bf и tf) наибольшее влияние на вес оказывает высота стенки балки hw или близкая к ней высота сечения h. Как известно ([2], c. 197-199, [3], с. 218-219), высота сечения, при которой достигается наименьший расход металла (наименьший вес) или оптимальная высота, равна:
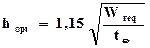 (6.14)
(6.14)
где Wreq=Mmax / Rygc (6.15)
tw= (7 + 3 hпр) /10 (см), но не менее 0.8 см (6.16)
hпр = ( 1/10 ¸ 1/12 ) L (м)(6.17)
Расчетное сопротивление материала Ry для подстановки в формулу (6.15) принимается по таблице 51 [1] для выбранной стали и толщины листового проката 20 – 40 мм. Толщину стенки tw, определенную по формуле (6.16) перед подстановкой в формулу (6.14) следует округлить до стандартной толщины листового проката в сантиметрах. Отношение высоты балки hopt, определенной по формуле (6.14), к толщине стенки tw,подставленнойв формулу,должно находиться в пределах величин, указанных в таблице 4, в противном случае необходимо изменить tw и вновь вычислить величину hopt.
График зависимости между высотой балки и ее весом (рис.6 а) в области минимума меняется очень плавно, поэтому отклонения до 15 % от оптимальной высоты как в ту, так и в другую сторону не приводят к существенному увеличению веса балки.
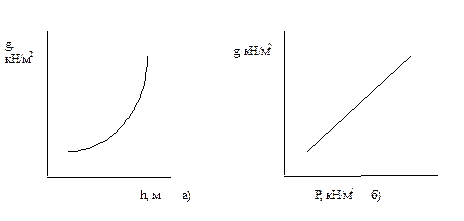 Рис. 6 а- график зависимости между высотой балки и ее весом; б- график зависимости расхода стали и нормативной нагрузки балки.
Рис. 6 а- график зависимости между высотой балки и ее весом; б- график зависимости расхода стали и нормативной нагрузки балки.
Таблица 4
Дата добавления: 2020-02-05; просмотров: 651;











