Понятие о теории подобия и ее применении в исследовании теплоотдачи

Теория подобия изучает подобные явления. Какие же явления называются подобными? Из геометрии мы знаем, что геометрически подобными фигурами являются те, для которых выполняется пропорциональность линейных размеров. Например, два треугольника считаются подобными, если отношения их всех сходственных сторон равны, т. е.

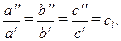
В этом случае величину 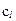принято называть константой (или постоянной) геометрического подобия.

Две различные системы координат являются также геометрически подобными, если выполняется подобие координат сходственных точек этих систем, т. е. если

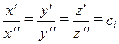
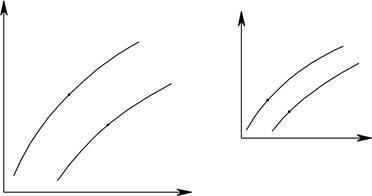
Подобными могут быть и поля физических величин. Рассмотрим, например, поля температур в двух различных, но подобных системах координат (рис. 11.4).

y'

y''

Ta' = const

Ta'' = const

a'

Tb'' = const

b''

a''

b'

Tb' = const

x''

x'

Рис. 11.4. Подобные поля температур

Эти поля являются подобными, если выполняется условие

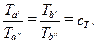(11.2)

В целом и явления называются подобными, если подобны поля, описывающие эти явления.

При этом необходимо обязательное выполнение двух условий:

1) должно соблюдаться геометрическое подобие;

2) явления должны рассматриваться в сходственные моменты времени.

Теория подобия широко используется при рассмотрении задач теплообмена, в частности, для определения коэффициента теплоотдачи.

Как было сказано выше, коэффициент 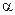зависит от целого ряда факторов, и его величина определяется экспериментальным путем.

В каких же случаях допускается переносить результаты эксперимента на реальный объект? Только в тех случаях, когда рассматриваются подобные процессы. Скажем, что для определения коэффициента теплоотдачи от трубопровода с горячей водой к прилегающему к нему грунту можно провести эксперимент на модели. Но при этом, помимо геометрического подобия (подобие диаметров и толщин трубопровода), условию (16.2) должны удовлетворять такие физические величины как скорость потока, материал трубопровода, теплофизические свойства грунта, вязкость жидкости и т. д. Только в этом случае будет справедлива зависимость:

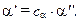
Однако и здесь возникает сложность в определений константы подобия .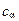

Поскольку в физических явлениях все величины, описывающие их, связаны между собой какими-то уравнениями, то некоторая зависимость должна быть и у констант подобия. Покажем это на простейшем примере. Рассмотрим два подобных треугольника, для которых, как видно из зависимости

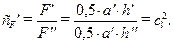
константа подобия площадей равна квадрату константы геометрического линейного подобия.

Следовательно, константы подобия, в свою очередь, могут быть связаны в некоторых безразмерных комплексах, которые называются критериями подобия.

Критерии подобия

Критерии подобия — это безразмерные комплексы, составленные из разноименных физических величин, описывающих данное явление и связанных взаимными уравнениями.