Стационарная теплопроводность плоской стенки

Простым примером задач теплопроводности является задача о теплопередаче через плоскую стенку, плоский слой жидкости или газа.

В качестве примера рассмотрим здесь только плоскую стенку (рис. 10.4) толщиной 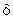, выполненную из однородного материала 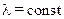. На поверхностях стенки поддерживаются постоянные температуры. При этом теплота передается слева направо. В этом случае имеет место изменение температуры только вдоль оси х, которая направлена, как показано на рис. 10.4.

Таким образом, здесь рассматривается одномерная задача. Граничные условия для этой задачи: на левой поверхности при 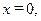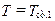, на правой поверхности при .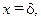

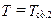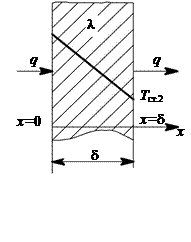
	Тст.1

Рис. 10.4. Теплопроводность через плоскую стенку

Рассмотрим стационарную задачу, для которой согласно определению 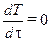(т. е. 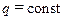). Из выражения (10.6) следует 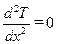. Проинтегрировав это выражение, получим

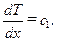(10.8)

Проинтегрировав выражение (10.8), окончательно получаем

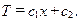(10.9)

Определим постоянные интегрирования с₁ и с₂. Для граничного условия при x=0 из (10.9) следует

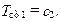(10.10)

Для граничного условия при 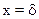с учетом (10.10) из (10.9) следует

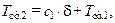
откуда видно, что

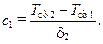(10.11)

Окончательно, подставив выражения (10.10) и (10.11) (с учетом того, что 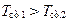) в выражение (10.9), получаем закон изменения температуры по толщине стенки:

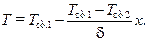(10.12)

Как видно из выражения (10.12), это изменение носит линейный характер.

Определим удельный тепловой поток, проходящий через стенку, для чего воспользуемся законом Фурье (10.2). Причем в этом выражении 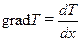. Определив первую производную по x в выражении (10.12), окончательно имеем

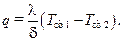(10.13)

Величину 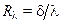в выражении (10.13) часто называют тепловым сопротивлением. С учетом 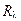выражение (10.13) напоминает хорошо известный закон Ома для участка цепи

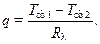
Рассмотрим теплообмен через плоскую многослойную стенку (рис. 10.5).

Поскольку рассматривается стационарная задача, то тепловой поток в каждом слое есть величина постоянная:

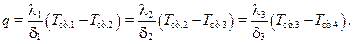(10.14)

Выражение (10.14) можно преобразовать к следующему виду:

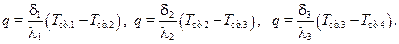(10.15)

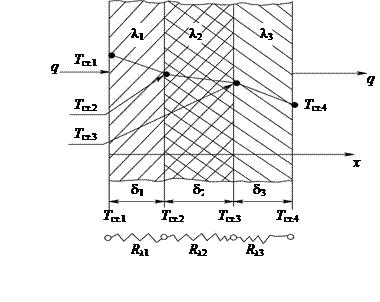Рис. 10.5. Теплопроводность через плоскую многослойную стенку

Сложим левые и правые части выражения (10.15) и получим

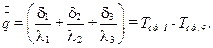(10.16)

Из выражения (10.16) легко получить формулу, справедливую для n-слойной пластины

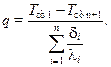(10.17)

Как видно из (10.17), здесь можно провести аналогию с законом Ома для участка цепи с последовательно включенными сопротивлениями.