Примеры критериальных уравнений теплоотдачи

Практическая ценность теории подобия заключается в том, что она позволяет результаты эксперимента, полученные на модели, перенести на реальный объект. При этом рассматриваемое явление может быть описано не уравнением или системой уравнений процесса, как правило, довольно сложными, а более простым критериальным уравнением. Кроме того, полученное критериальное уравнение будет справедливо для всех подобных явлений. Например, для явлений диффузии, теплопроводности, описываемых подобными уравнениями.

Критериальное уравнение отличается от уравнения процесса тем, что в него входят не чисто физические параметры, а критерии подобия, содержащие эти параметры. При этом число критериев подобия становится значительно меньше числа физических параметров, в них входящих.

При этом вид уравнения, как правило, упрощается в этом тоже преимущество применения теории подобия.

Действительно, коэффициент теплоотдачи α зависит от целого ряда факторов

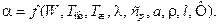(12.1)

Если применить критерии подобия, записанные через эти же физические параметры, то получим более упрощенную по сравнению с (12.1) критериальную зависимость

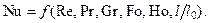(12.2)

Здесь l/l₀ — критерий геометрического подобия.

Уравнение (12.2) называется критериальным уравнением теплоотдачи.

В свою очередь, и зависимость (12.2) может быть значительно упрощена.

Действительно, если рассматривать только установившийся режим теплоотдачи, то нет смысла учитывать критерии Fo и Нo. Таким образом, для стационарных процессов уравнение (12.2) примет вид

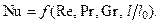(12.3)

При турбулентном стационарном режиме вынужденного течения среды можно не учитывать критерий Gr, так как влияние сил тяжести здесь мало, поэтому

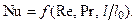(12.4)

При свободной конвекции скорости течения жидкости малы, и можно пренебречь критерием Re, который будет иметь незначительную величину. Тогда критериальное уравнение принимает вид

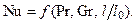(12.5)

В указанных выше критериальных уравнениях все критерии подобия, стоящие в правой части, называются определяющими. Они могут быть определены по известным физическим и геометрическим зависимостям, измеренным до или в ходе проведения эксперимента.

Кроме того, в ходе эксперимента устанавливается конкретный вид функциональной связи в уравнении подобия. После этого, решив полученное уравнение, можно определить значение Nu (а, следовательно, и α) для данного процесса. Таким образом, критерий Nu, в свою очередь, является определяемым критерием.

Поясним вышесказанное на примере. Рассмотрим течение жидкости в трубе. В случае ламинарного режима течения экспериментально получена следующая зависимость (формула академика Михеева M.А.):

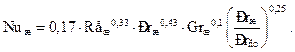(12.6)

Здесь Pr_ж — критерий Прандтля, вычисленный для жидкости при температуре в ядре потока; Pr_ст — критерий Прандтля, определенный для жидкости при температуре стенки.

Как видно, в ходе эксперимента для уравнения (12.3) получены конкретные значения коэффициентов и показателей степени в выражении для критерия Нуссельта.

Зададимся целью определить значения коэффициента теплоотдачи α при различных скоростях течения жидкости W_ж.

Меняя скорость течения жидкости, каждый раз в ходе экспери­мента определяем температуру жидкости Т_ж в ядре потока и температуру стенки Т_ст. По теплофизическим справочникам найдем значения ν, а , β при данных значениях температуры.

После этого, вычислив значения

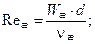
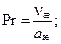
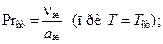
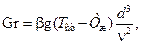
находим значение Nu_ж.

Коэффициент теплоотдачи определяется как

.

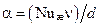Теперь эти значения α могут быть перенесены на все подобные процессы.

В качестве примера приведем еще ряд видов критериальных уравнений, представленных на рис. 12.1, 12.2.

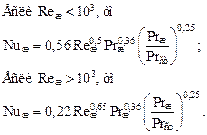
Рис. 12.1. Критериальные уравнения при обтекании труб, расположенных в коридорном порядке

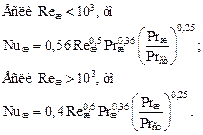
Рис. 12.2. Критериальные уравнения при обтекании труб, расположенных в шахматном порядке