Вывод уравнения теплопроводности плоской стенки

Запишем уравнение Фурье в развернутом виде

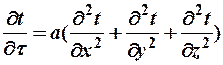
При стационарном режиме температура в различных точках постоянна во времени, т.е

Температурное поле одномерно (плоская стенка) .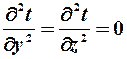

Т.о. уравнение Фурье приобретает вид: d²t/dx²=0.

Проинтегрируем дважды: dt/dx = C₁; t = C₁x+C₂. C₁ и С₂ найдем из условий на границе: х=0; х=d. При х=0 t_ст1=С₂, а при х=d t_ст2= C₁d+ t_ст1;

C₁=( t_ст2- t_ст1)/d; В результате получим

t=x(t_ст2- t_ст1)/d+ t_ст1 (8)

Температура по толщине стенки х меняется линейно, температурный градиент сохраняет постоянное значение. Подставим полученное значение градиента температуры в (4)-з. Фурье и получим уравнение теплопроводности плоской стенки при стационарном тепловом режиме

dQ=l/d( t_ст1 - t_ст2)dFdt .

Q=l/d( t_{ст 1} - t_ст2)Ft (9).

Здесь l/d - термическая проводимость стенки.

Теплопроводность цилиндрической стенки (самост.)

В тепловых процессах одновременно с теплопроводностью и конвекцией почти всегда имеет место тепловое излучение, причем, чем выше температура тела, тем больше тепла оно передает в виде теплового излучения.

Тепловое излучение

- это процесс распространения энергии в форме электромагнитных волн.