Дифференциальное уравнение теплопроводности

Дифференциальное уравнение теплопроводности является математическим выражением закона сохранения энергии в веществе, взаимодействие которого с внешней средой происходит без совершения какой-либо работы. При этом считается, что передача теплоты в веществе осуществляется только за счет теплопроводности.

Согласно первому закону термодинамики

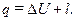
Здесь 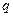— суммарное количество теплоты, подведенной к телу, 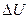— изменение внутренней энергии; l — работа внутренних сил тела, совершенная над окружающей средой (как было сказано выше, ).

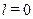В общем случае величина q складывается из теплоты, подведенной к телу и отведенной от него в окружающую среду через поверхность S, и теплоты, генерируемой внутри рассматриваемого объема (скажем, за счет химической реакции или нагрева в результате пропускания электрического тока). В целях упрощения вывода уравнения теплопроводности мы последнюю составляющую теплоты учитывать не будем. Такое упрощение вполне справедливо для большинства процессов, протекающих, как правило, без генерирования тепловой энергии.

Согласно закону Фурье, количество теплоты, подводимое к стенке справа (рис. 10.3), определится выражением

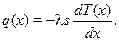
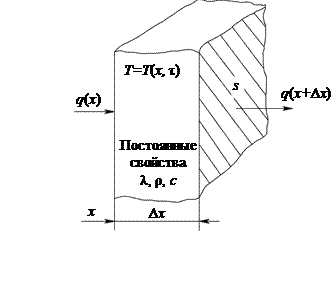
Рис. 10.3. К выводу дифференциального уравнения теплопроводности

Теплота, которая отводится от стенки слева следующим образом

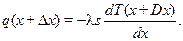
Теплота, которая поглотится рассматриваемым объемом, идет на изменение внутренней энергии тела. Она определяется как

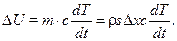
Здесь 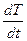— скорость изменения температуры в единице объема.

Из баланса энергии для рассматриваемого объема следует

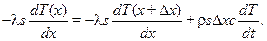(10.3)

Разделив выражение (10.3) на 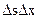выполнив несложные преобразования, получим

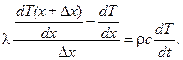(10.4)

Если перейти к пределу при 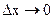, то левая часть равенства (10.4) станет (по определению) второй производной температуры по x и равенство примет вид

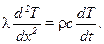(10.5)

Введем обозначение

,

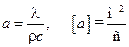тогда выражение принимает окончательный вид дифференциального уравнения теплопроводности для одномерного поля температуры:

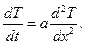(10.6)

Если рассмотреть подобную задачу для трехмерного поля, т.е. учесть, что 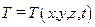, то получим следующую форму дифференциального уравнения теплопроводности.

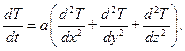(10.7)

В выражениях (10.6) и (10.7) коэффициент a получил название коэффициента температуропроводности. Нетрудно убедиться, что коэффициент a имеет размерность м²/с.

Коэффициент температуропроводности характеризует скорость изменения температуры в нестационарных тепловых процессах и является мерой теплоинерционных свойств вещества. Величины коэффициента температуропроводности для различных веществ при различных значениях температуры приводятся в теплофизических справочниках.