Давление струи на плоскую и криволинейную поверхности.
На рисунке показана (лоток) труба криволинейной формы.
Жидкость входит через сечение 1-1 со скоростью 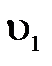 , составляющий с осью Х угол
, составляющий с осью Х угол 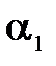 и выходит через сечение 2-2 со скоростью
и выходит через сечение 2-2 со скоростью 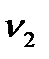 , составляющей с осью Х угол
, составляющей с осью Х угол 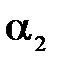 скорость потока меняет свою величину и направление между сечениями первым и вторым под действием сил реакции со стороны стенок лотка (трубы).
скорость потока меняет свою величину и направление между сечениями первым и вторым под действием сил реакции со стороны стенок лотка (трубы).
Если составить уравнения изменения количества движения в проекциях на оси Х, то из этих уравнений можно получить проекции сил реакции на те же оси. Проекция изменения количества движения на ось Х за время dt равна проекции импульса силы реакции на ту же ось Х:
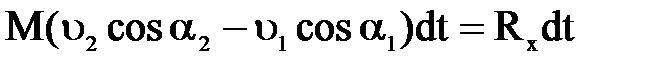 ,
,
где М-масса жидкости, протекающей за единицу времени, равная
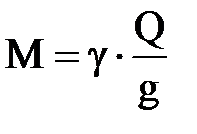 ;
;
Rx-проекция силы реакции на ось Х.
Проекция изменения количества движения на ось Z выразится следующим уравнением:
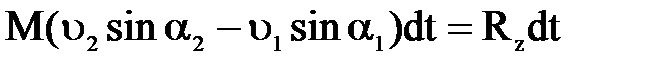 .
.
Если вместо сил реакции стенок лотка (трубы) написать проекции сил давления жидкости на стенки, т.е. заменить Rx на –Px и Rz на Pz и отнести уравнения к единице времени, то получим:
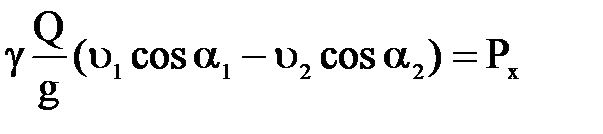
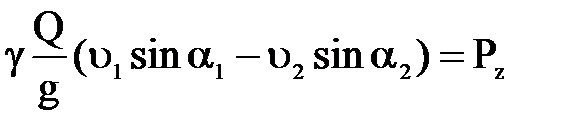
Зная проекции сил давления потока жидкости на стенки можно определить общее гидродинамическое давление:
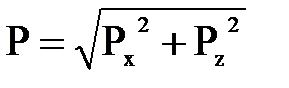
Используем полученные уравнения для конкретных задач.
Жидкость входит в верхнее (первое) сечение со скоростью 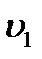 , образующей с осью Х угол
, образующей с осью Х угол 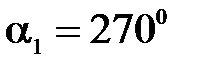 и выходит через боковое сечение со скоростью
и выходит через боковое сечение со скоростью 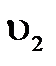 образующей с осью Х угол
образующей с осью Х угол 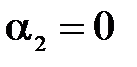 ,так как сечение колена не изменяется, то скорость
,так как сечение колена не изменяется, то скорость 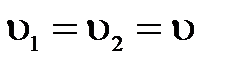 . Тогда формула примет вид:
. Тогда формула примет вид:
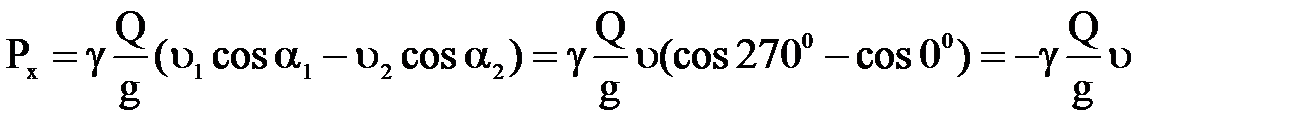 ;
;
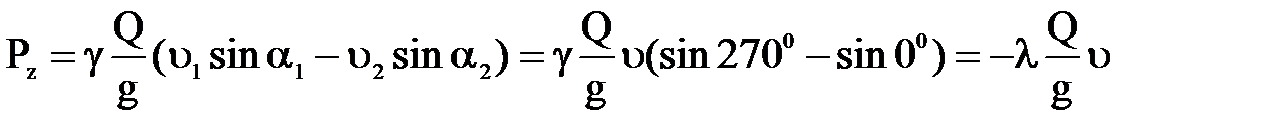 ,
,
а общее гидродинамическое давление равно 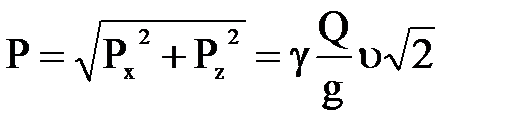
где Рх и Рz численно равны и имеют знак минус, это значит что направление проекции сил давления обратно направлению координатных осей.
Давление Рz направлено по линии действия скорости 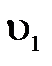 и является активным; давление
и является активным; давление 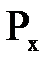 направленно обратно направлению скорости
направленно обратно направлению скорости 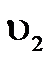 и является реактивным.
и является реактивным.
Активное давление потока (гидродинамическое давление) необходимо учитывать во время прокладки трубопроводов при больших величинах скоростей. В местах поворота трубопроводов, в особенности при углах поворота в 900, гидродинамическое давление достигает относительно больших величин по сравнению с гидростатическим давлением в трубопроводах малого диаметра.
Рассмотрим давление струи, вытекающей из насадки или отверстия на плоские и криволинейные стенки, поставленные на пути движения струи.
Резервуар из отверстия которого под напором Н вылетает струя со скоростью 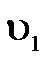 . При установке небольшой пластинки струя обтекает ее, при этом угол отклонения струи от первоначального направления
. При установке небольшой пластинки струя обтекает ее, при этом угол отклонения струи от первоначального направления 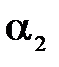 .
.
Гидродинамическое давление на пластинку 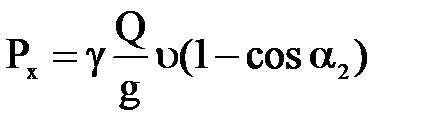 ,
,
так как 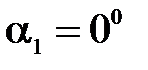 и
и 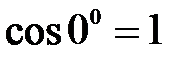 ; кроме того,
; кроме того, 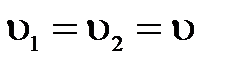 (скорость меняет лишь свое направление, величина же ее остается неизменной).
(скорость меняет лишь свое направление, величина же ее остается неизменной).
При приближении пластинки к отверстию или при большей ее величине угол 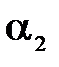 становится равным 900,
становится равным 900, 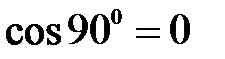 .
.
В этом случае 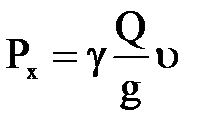 .
.
Так как 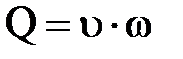 , то
, то 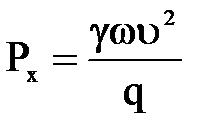 .
.
Сравним величину гидродинамического давления 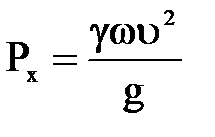 с величиной гидростатического давления Р при размере площадки ω и напоре Н:
с величиной гидростатического давления Р при размере площадки ω и напоре Н:
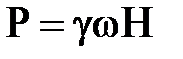
Если подставить в последнюю формулу вместо величины Н соответствующей ей скоростной напор
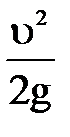 , то
, то 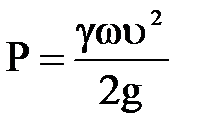 .
.
Из сравнения величин 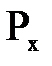 (гидродинамическое давление) и Р (гидростатическое давление) можно сделать вывод, что гидродинамическое давление в два раза больше гидростатического.
(гидродинамическое давление) и Р (гидростатическое давление) можно сделать вывод, что гидродинамическое давление в два раза больше гидростатического.
Если изогнуть пластинку (рис. в), то угол 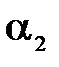 станет больше 900 и
станет больше 900 и 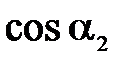 будет равен -
будет равен - 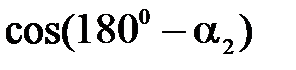 , тогда
, тогда 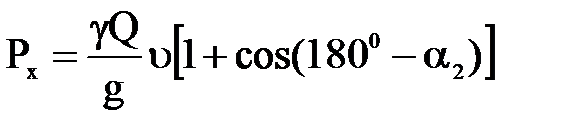 .
.
Если изогнуть пластинку так, что струя, ударяясь о пластинку, будет изменять свое первоначальное направление на 1800 (г), то  , а
, а
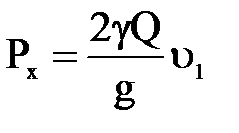 ,
,
т.е. в данном случае гидродинамическое давление будет в четыре раза больше гидростатического. Такие изогнутые лопатки устраивают в активных гидротурбинах.
Мощность струи, ударяющейся о пластинку, движущуюся со скоростью u, определяются по формуле 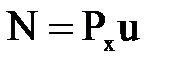 .
.
Для того чтобы мощность N была положительной, необходимо, чтобы направление скорости u совпадало с направлением 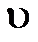 , при этом скорости u может изменяться в пределах
, при этом скорости u может изменяться в пределах 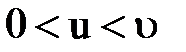 , так как при
, так как при 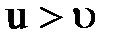 струя не будет производить никакой работы. При движении пластинки со скоростью u давление
струя не будет производить никакой работы. При движении пластинки со скоростью u давление
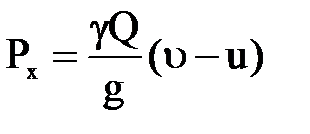 ,
,
а соответствующая ей мощность 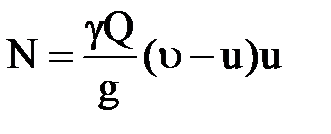 .
.
Для определения возможно max мощности струи, зависящей в основном от соотношения между величинами скоростей u и υ.
Найдем первую производную мощности по скорости u:
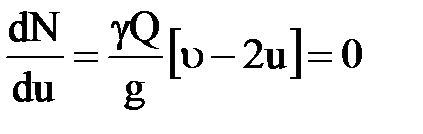 .
.
Вторая производная 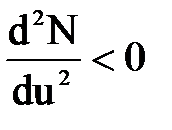 ; следовательно, написанное условие соответствует max мощности, так как
; следовательно, написанное условие соответствует max мощности, так как 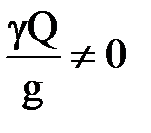 , то
, то 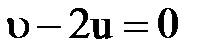 , или
, или 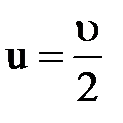

Дата добавления: 2016-06-15; просмотров: 2286;











