Метод анализа размерности (ПИ- ТЕОРЕМА).

Методы подобия и размерностей тесно связаны между собой, так как оба требуют отчетливого представления о механизме рассматриваемого явления.

Однако для применения теории подобия нужны уравнения, определяющие процесс, а метод анализа размерностей применяется, когда уравнения процесса неизвестны.

С помощью этого метода обрабатывают данные опытов и делают последующие обобщения. Начало общей теории этого метода было впервые положено в 1911 г. русским ученным Г.А. Федерманом, доказавшим теорему подобия - Пи-теорему: всякое уравнение, выражающее некоторую физическую закономерность и поэтому не зависящее от выбора системы единиц измерения, связывающее собой N физических величин среди которых n величин обладают независимыми размерностями, может быть преобразовано в уравнение связывающее (N-n) независимых безразмерных комплексов, составленных из N упомянутых физических величин.

Суть этой теоремы заключается в следующем.

Пусть W является функцией N размерных величин:

W=f( ).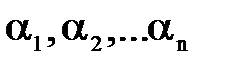

Можно доказать, что эту зависимость можно заменить критериальным уравнением

,

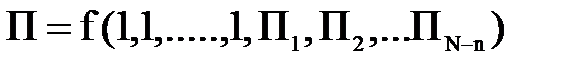где роль размерных величин играют 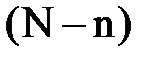безразмерных величин. Если основная система состоит из трех единиц (масса, длина, время), то n=3 и вместо величин рассматриваемое явление представляется в виде зависимости между безразмерными комплексами этих величин.

Таким образом, в составленном путем логических рассуждений уравнении, характеризующим данное явление, размерности величин в правой и левой частях, выраженные через размерности основных физических величин (масса М, длина 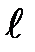и время Т) должны соответствовать друг другу.

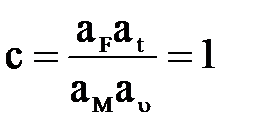
с-называется индикатором подобия.

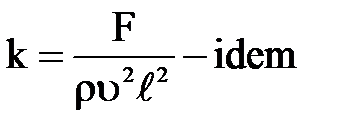
К-критерий подобия

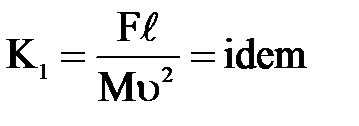
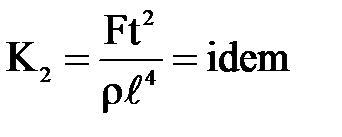
1. Если явления подобны, то индикаторы подобия равны единице.
2. У подобных явлений критерии равны между собой.