Два потока будут геометрически подобными, если между их соответствующими линейными размерами существует постоянное соотношение

,

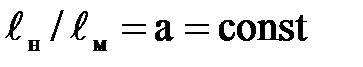где а- линейный масштаб, показывающий во сколько раз размеры модели 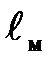уменьшены по сравнению с размерами натуры .

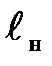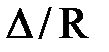Отметим, что в геометрически подобной модели русла, все размеры, в том числе и высота выступов шероховатости , должна быть меньше, чем в натуре в а раз и, следовательно, в подобных потоках относительная шероховатость остается постоянной, такой же как в натуре, то есть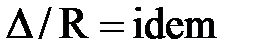

Должны быть также постоянными соотношения площадей 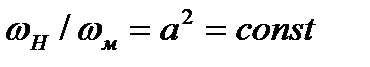и объемов .

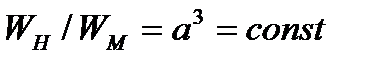Два потока будут кинематические подобны при подобии полей скоростей и ускорений натуры и модели, которое выполняется если скорость 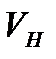и и 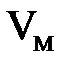ускорения 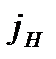и 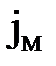в сходственных точках натуры и модели находятся в одинаковых соотношениях, то есть существуют масштабы скоростей а_v и ускорений а_j :

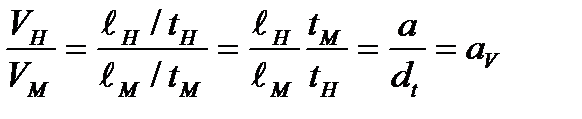
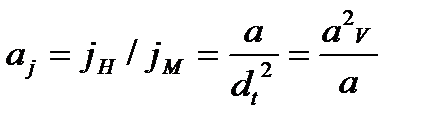
При этом 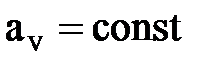и 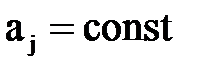. Кинематическое подобие обязательно включает в себя геометрическое подобие.

Для динамического подобия необходимо, чтобы все силы, действующие в подобных точках модели и натуры на частицы жидкости, отличались между собой только постоянными масштабами при равенстве углов, характеризующих направление этих сил.

Другими словами, явления динамически подобны, если физическая природа действующих на жидкость сил одинакова и векторы образуют геометрически подобные силовые многоугольники.

На любую частицу жидкости в общем случае действуют следующие силы. Сила тяжести, пропорциональная плотности жидкости, ускорению свободного падения g и объему W (или кубу линейного размера частицы ):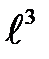

~

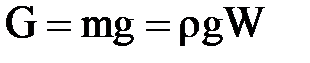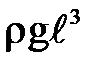
Сила давления, пропорциональная гидродинамическому давлению p и площади S (или квадрату линейного размера частицы ):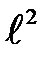

~

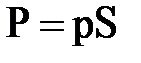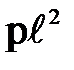
Сила трения, пропорциональная вязкости частицы жидкости 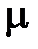, скорости ее движения V и линейному размеру :

~

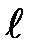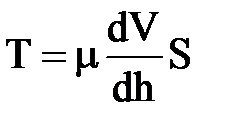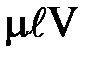
Равнодействующая этих сил F, согласно второму закону ньютона, равна произведению массы на ускорение:

~

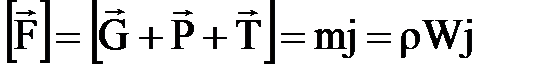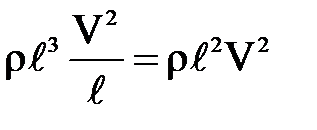
Эта равнодействующая численно равна силе инерции:

~

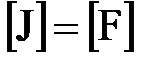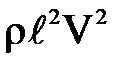
Из условия подобия отношения всех пар сходственных сил натуры и модели равны

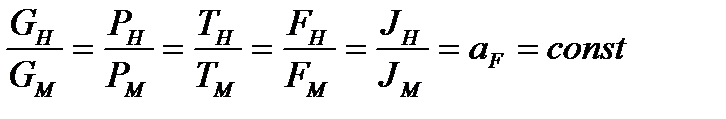(1)

где 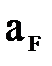- масштаб сил, то есть число, показывающее во сколько раз силы в натуре (с индексом «Н») больше соответствующих в модели.

Величины a, а_V и а_F называются масштабными множителями. Выбор всех масштабных множителей для подобных потоков не произволен, так как между ними существует определенная взаимосвязь.

Равнодействующая всех сил, действующих на произвольно взятую в потоке частицу жидкости, выражается в виде .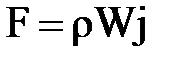

Следовательно, равнодействующие силы, действующие на две сходные частицы жидкости потока в натуре и модели равны:

,

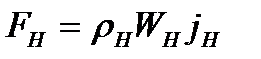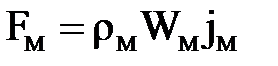
Если выразить их соотношение в масштабных множителях, то получим

,

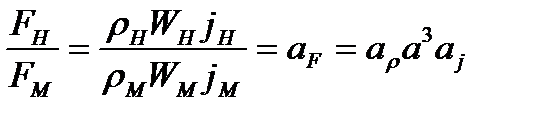где 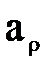- масштабный множитель плотности.

Учитывая, что масштабный множитель ускорения 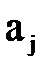выражается через масштабные множители скорости 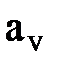и длины а в виде 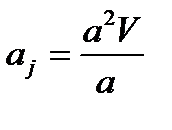, получим что

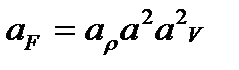
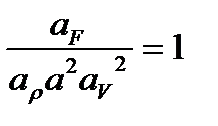- закон подобия Ньютона в масштабных множителях.

Выражая масштабные множители соответствующими отношениями, получим

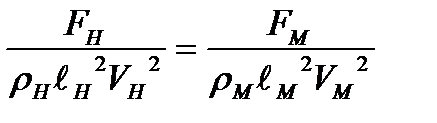, или

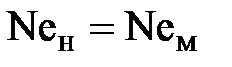, то есть ,

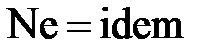где величина 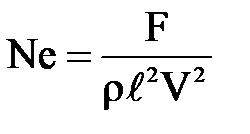- называется критерием Ньютона.

Критерий Ньютона можно записать и в другом виде, умножив числитель и знаменатель на 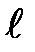, и тогда 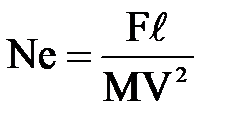так как .

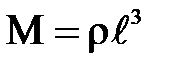При этом закон подобия Ньютона в физических величинах записывается в виде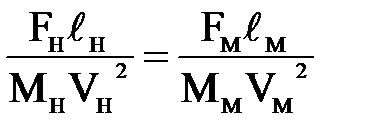

Гидродинамическое (гидравлическое) подобие потоков обеспечивается равенством критериев Ньютона модели и натуры .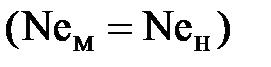

Критерии гидродинамического подобия.

Условием гидродинамического подобия является равенство на модели и в натуре отношений всех сил (тяжести, давления, инерции, трения, поверхностного натяжения и др.). Вследствие физических особенностей этих сил полное подобие всех сил практически недостижимо и необязательно. Поэтому устанавливают критерии подобия для частных случаев, когда в качестве преобладающей, принимается какая-нибудь одна из действующих сил.

Критерий Фруда.

Если преобладает действие сил тяжести, то необходимо выполнение условия,

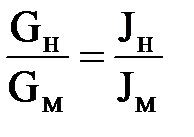или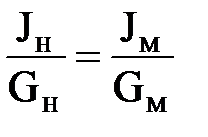

Следует ,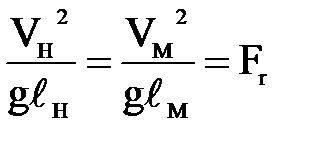

где F_r- число Фруда или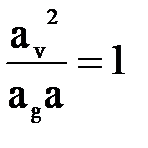

Следовательно, геометрически подобные потоки можно считать гидродинамически подобными, если будут равны числа Фруда для сходственных сечений обоих потоков:

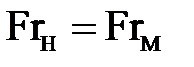или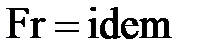

При этом справедливы следующие соотношения для скоростей и расходов

;

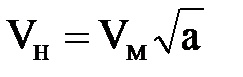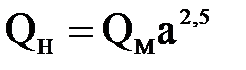
Масштабный множитель для времени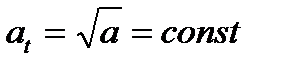

При моделировании по Фруду справедливо равенство гидравлических уклонов 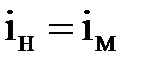, что соответствует турбулентному режиму движения в квадратичной области сопротивления.