ТЕМА5. ДВИЖЕНИЕ ЖИДКОСТИ В НАПОРНОМ ТРУБОПРОВОДЕ.

Лекция 14. Гидравлический расчет трубопровода. Основное расчетное уравнение для простого трубопровода. Уравнение Лейбензона. Сложные трубопроводы.

В современной технике применяются трубопроводы для перемещения разнообразных жидкостей, изготовляемые из различных материалов.

В зависимости от геометрической конфигурации различают простые и сложные трубопроводы.

Простым называют трубопровод, состоящий из одной линии труб, не имеющий боковых ответвлений, т.е. трубопровод с одинаковым расходом на всем пути движения жидкости от места ее забора А до пункта потребления В. Такой трубопровод может быть выполнен из труб одного диаметра по всей длине, или из участков труб различной длины и диаметра.

Сложным называют трубопровод, состоящий из основной магистрали и ряда отходящих от нее ответвлений.

Различают следующие виды:

а) параллельные, когда к основной магистрали М параллельно подключены одна или несколько труб.

б) разветвленные, в которых жидкость из магистрали М подается в боковые ответвления, обратно в магистраль она не поступает.

в) кольцевые, представляющие собой замкнутую сеть в кольцо, питаемую от основной магистрали М.

В напорных трубопроводах жидкость находится под избыточным давлением и полностью заполняет все поперечное сечение.

Для расчета трубопроводов исходным является уравнение Бернулли, из которого следует, что разность значений напора Н₁ в сечении 1-1 и Н₂ в сечении 2-2 затрачивается на преодоление гидравлических сопротивлений при движении жидкости на участке между этими сечениями.

Таким образом, 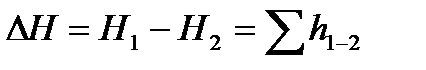, где .

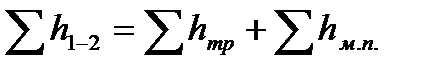При этом потери на трение определяются по формуле Дарси-Вейсбаха, 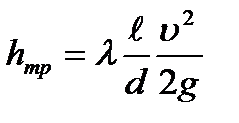, местные потери напора определяются по формуле .

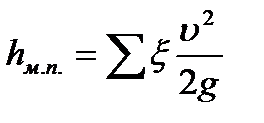При ламинарном режиме .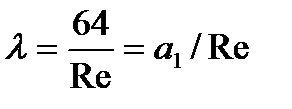

При турбулентном режиме для «гидравлически гладких» труб (закон сопротивления Блазиуса)

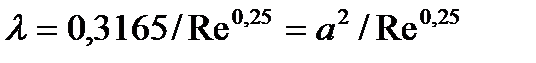
При турбулентном режиме в автомодельной области «вполне» шероховатых труб (квадратичный закон сопротивления) коэффициент не зависит от числа Рейнольдса, поэтому показатель степени у Re здесь следует положить равным 0. Если исходить из формулы Шифринсона, будем иметь

.

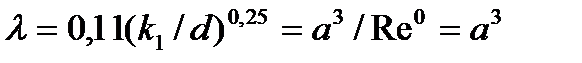Задача осложняется в случае турбулентного режима в доквадратичной области смешанного трения, в которой 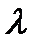одновременно является функцией и числа Рейнольдса и шероховатости стенок. Сохраняя и здесь для 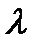формулу записи, по Белоусову можно принять:

.

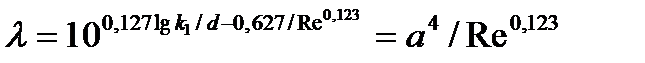Таким образом, имеем общую зависимость 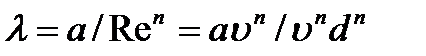справедливую для любых режимов движения жидкости. В ней коэффициент а и показатель степени n в зависимости от характера режима имеют различные значения. Подставив это выражение в формулу Дарси, имеем: .

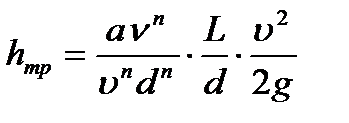С учетом того, что 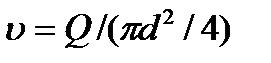получим общее выражение для потерь напора на трение (формула Л. С. Лейбензона).

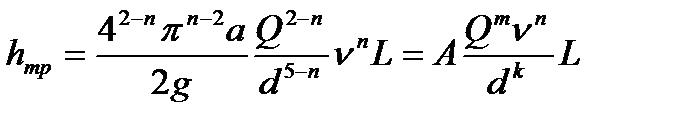, где ; ; .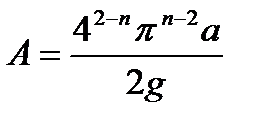

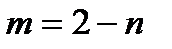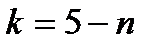Значения коэффициента А и показателей степени m, n и k для различных режимов движения жидкости можно найти в специальных таблицах.