ИСТЕЧЕНИЕ ЖИДКОСТИ ПРИ ПЕРЕМЕННОМ НАПОРЕ.
Рассмотрим истечение жидкости при переменном напоре из сосуда с произвольной формой поперечного сечения 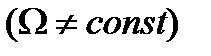 и наличием переменного притока жидкости в сосуд
и наличием переменного притока жидкости в сосуд 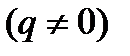 .
.
В общем виде уравнение неразрывности движения (уравнение баланса жидкости) для этой задачи можно записать так:
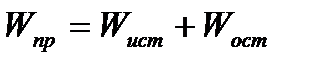 .
.
За бесконечно малый промежуток времени dt в сосуд поступил некоторый объем жидкости (объем притока): 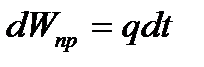 .
.
За этот же промежуток времени из сосуда вытечет некоторый объем жидкости (объем истечения) 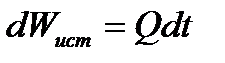 ,
,
где Q- расход жидкости.
Разность этих объемов и составит объем остатка
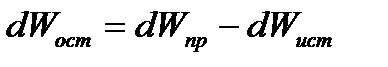 (1).
(1).
Объем остатка можно представить в виде произведения площади сечения сосуда  на приращение уровня жидкости в нем (то есть приращение напора) dz, где z – переменный напор жидкости в сосуде.
на приращение уровня жидкости в нем (то есть приращение напора) dz, где z – переменный напор жидкости в сосуде.
Тогда 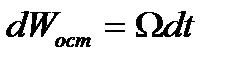 .
.
Подставляя полученный результат в (1) получим дифференциальное уравнение неразрывности движения для случая истечения жидкости при переменном напоре и наличии притока
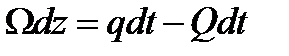 .
.
Из него следует, что 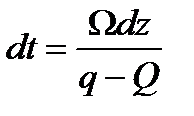 .
.
Получили основную зависимость для истечения жидкости из отверстий и насадков при переменном напоре.
Если площадь отверстия 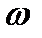 , а расход притока
, а расход притока 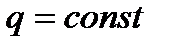 , то напор, при котором расход истечения будет равен постоянному расходу притока,
, то напор, при котором расход истечения будет равен постоянному расходу притока, 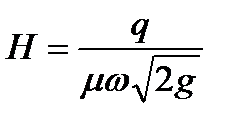 ;
; 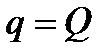 .
.
Если в какой либо момент времени фактический напор в сосуде z , то при z>Н расход истечения 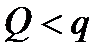 , и уровень жидкости в сосуде будет повышаться до тех пор, пока не станет равным Н, при
, и уровень жидкости в сосуде будет повышаться до тех пор, пока не станет равным Н, при 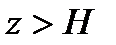 расход Q>q и уровень жидкости в сосуде будет понижаться до тех пор, пока не станет равным Н.
расход Q>q и уровень жидкости в сосуде будет понижаться до тех пор, пока не станет равным Н.
Определяя в каждый момент времени расход при переменном напоре по формуле: 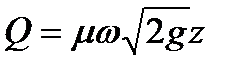 , справедливой для случая истечения при постоянном напоре, подставляя выражения для q и Q и интегрируя, найдем время Т изменения уровня жидкости в сосуде от z1 до z2. в общем случае истечения жидкости при наличии постоянного притока.
, справедливой для случая истечения при постоянном напоре, подставляя выражения для q и Q и интегрируя, найдем время Т изменения уровня жидкости в сосуде от z1 до z2. в общем случае истечения жидкости при наличии постоянного притока.
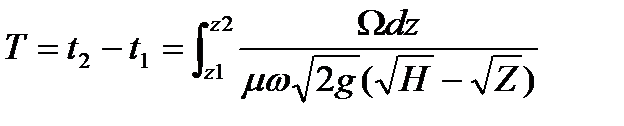 .
.
С изменением напора меняется коэффициент сжатия струи 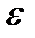 , и частично коэффициент скорости
, и частично коэффициент скорости 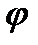 . Следовательно, в общем случае коэффициент расхода
. Следовательно, в общем случае коэффициент расхода 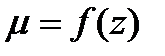 . Однако при истечении маловязкой жидкости коэффициент расхода меняется незначительно. Учитывая, что в условиях конкретных расчетов пределы изменения напора обычно не очень велики, а в таблицах приводятся осредненные, опытные значения коэффициента расхода, можно считать
. Однако при истечении маловязкой жидкости коэффициент расхода меняется незначительно. Учитывая, что в условиях конкретных расчетов пределы изменения напора обычно не очень велики, а в таблицах приводятся осредненные, опытные значения коэффициента расхода, можно считать 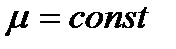 , и тогда время, за которое уровень жидкости в сосуде измениться от z1 до z2.
, и тогда время, за которое уровень жидкости в сосуде измениться от z1 до z2.
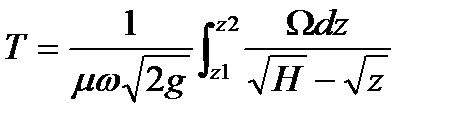 .
.
Для практического использования необходимо знать 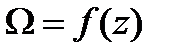 .
.
Водосливы.
Если в потоке жидкости со свободной поверхностью установить искусственную преграду, уровень жидкости перед этой преградой повысится, и жидкость будет переливаться через нее. Подобные преграды называют водосливами.
Водосливы классифицируются по ряду признаков. В зависимости от формы сливного напора, называемого гребнем водослива, различают следующие типы водосливов:
1) с тонкой стенкой или острой кромкой .
2) с широким пологом, на таком пологе устанавливается почти параллельное струйное течение жидкости.
3) практического профиля, имеющий криволинейные очертания, соответствующие нижней поверхности струи жидкости при переливе через острый порог.
Если длина гребня водослива меньше ширины преграждающего потока, то в зависимости от формы выреза в преграждающей стенке, водослив может быть прямоугольным, треугольным, трапециидальным и параболическим.
Основной задачей при расчете водослива является определение расхода жидкости, протекающей через него.
Рассмотрим прямоугольный водослив с тонкой стенкой.
По мере приближения к водосливу уровень свободной поверхности перед ним постепенно снижается и принимает форму кривой спада. Снижение уровня перестает быть практически заметным на расстоянии от водослива равном 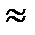 3 м. Н – глубина погружения гребня водослива – напор на водосливе.
3 м. Н – глубина погружения гребня водослива – напор на водосливе.
Истечение рассматриваем как истечение из большого прямоугольного отверстия в тонкой боковой стенке.
Воспользуемся формулой: 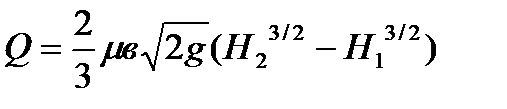 .
.
Принимаем Н1=0, а Н2 заменяем на Н, что соответствует случаю водослива, в этом случае пределы интегрирования при учете скорости подхода будут равны: верхний предел – Н+ 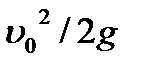 , нижний
, нижний 
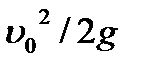 и
и 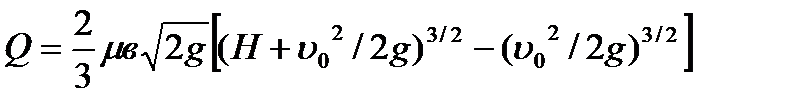 ,
,
Где в – ширина порога водослива (ширина отверстия); Н – напор над пологом водослива; 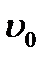 - скорость подхода к гребню;
- скорость подхода к гребню;
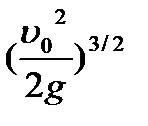 - пренебрегая, введем коэффициент
- пренебрегая, введем коэффициент 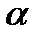 , учитывающий неравномерность распределения скоростей и выражая
, учитывающий неравномерность распределения скоростей и выражая 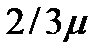 через m (коэффициент расхода водослива)
через m (коэффициент расхода водослива)
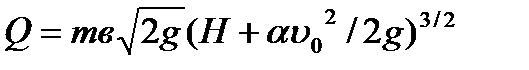 .
.
Если не учитывать 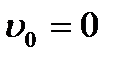 , то
, то 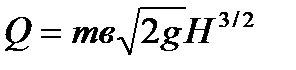 .
.
Коэффициент расхода m определяется опытным путем и зависит от напора Н и высоты водосливного порога р, его можно посмотреть в справочнике.
Для измерения расхода в трапециидальном водосливе в тонкой стенке 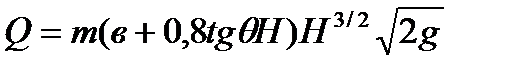 ,
,
где 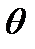 - угол наклона боковой стенки; в – ширина водослива по низу; m – коэффициент расхода, определяется опытным путем.
- угол наклона боковой стенки; в – ширина водослива по низу; m – коэффициент расхода, определяется опытным путем.
При 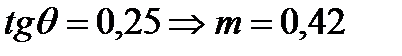 .
.
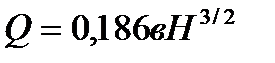 .
.
Для водослива треугольной формы 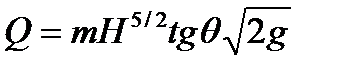 .
.
Дата добавления: 2016-06-15; просмотров: 2638;











