РАСЧЕТ ПРОСТОГО ТРУБОПРОВОДА.
Пусть имеются два резервуара: питающий А и расходующий В с установившейся разностью уровней  , соединенные между собой простым трубопроводом длиной L и постоянным диаметром d. Пусть резервуары открыты, и давление на свободных поверхностях жидкости в них равно атмосферному. Средние скорости в сечениях на поверхности жидкости в резервуарах обозначим
, соединенные между собой простым трубопроводом длиной L и постоянным диаметром d. Пусть резервуары открыты, и давление на свободных поверхностях жидкости в них равно атмосферному. Средние скорости в сечениях на поверхности жидкости в резервуарах обозначим 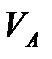 и
и 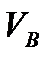 . Составим для указанных сечений уравнение Бернулли
. Составим для указанных сечений уравнение Бернулли
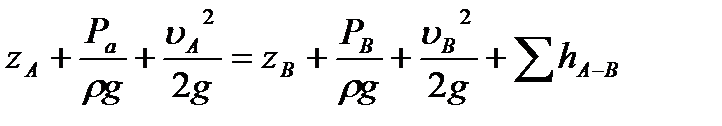 .
.
Пренебрегая в этом уравнении значениями скоростных напоров 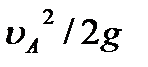 и
и 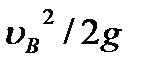 вследствие их малости по сравнению с остальными величинами, а так же учитывая, что
вследствие их малости по сравнению с остальными величинами, а так же учитывая, что 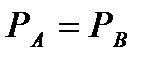 , получаем
, получаем 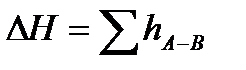 .
.
Полная потеря напора определяется как сумма потерь на трение по длине трубопровода 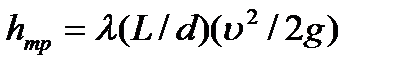 и местных потерь
и местных потерь 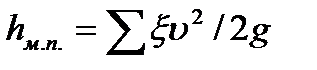 ;
;
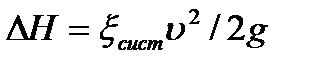 , где
, где 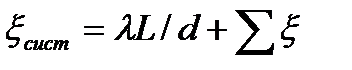 .
.
Из последнего уравнения по заданному  легко определить скорость и расход жидкости:
легко определить скорость и расход жидкости:
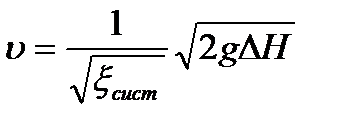 ,
,
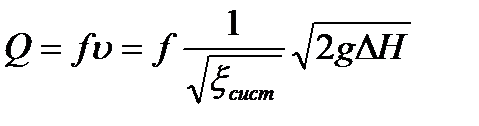 .
.
При большой длине трубопровода, когда местными потерями по сравнению с потерями на трение по длине можно пренебречь, расход определяется непосредственно по формуле Лейбензона.
В частном случае квадратичного закона сопротивления его можно найти так же из более простого выражения 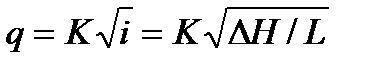 (1)
(1)
Указанные уравнения позволяют определить так же диаметр трубопровода (в том случае, когда перепад напоров, длина трубопровода, расход жидкости и ее вязкость известны). Наиболее просто это задача решается при квадратичном законе сопротивления- из формулы (1) находят модуль расхода и по соответствующим таблицам устанавливают стандартный диаметр трубопровода, отвечающий ближайшему (к полученному расчетом) большему значению этого модуля. В такой постановке задача о гидравлическом расчете трубопровода встречается сравнительно редко, так как обычно диаметр трубы выбирают исходя из технико-экономических соображений.
Если трубопровод состоит из участков 1,2,3…n различной длины  ,
, 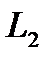 …
…  и разного диаметра
и разного диаметра 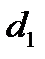 ,
, 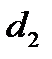 ….
…. 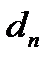 , последовательно соединенных между собой, задача решается аналогично предыдущей.
, последовательно соединенных между собой, задача решается аналогично предыдущей.
При таком последовательном соединении полная потеря напора на всем протяжении трубопровода от начальной его точки А до конечной В определяется как сумма потерь на отдельных участках
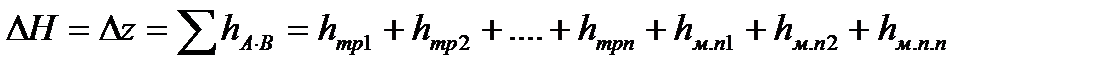
и может быть выражена через коэффициент сопротивления системы следующим образом: 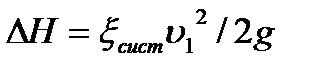 , где
, где 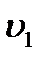 - скорость в каком-нибудь произвольно выбранном сечении трубопровода, а коэффициент сопротивления системы
- скорость в каком-нибудь произвольно выбранном сечении трубопровода, а коэффициент сопротивления системы
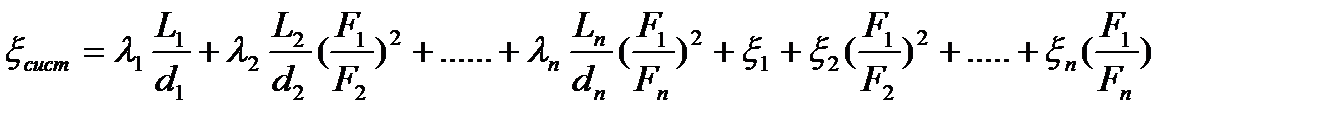 .
.
Если не учитывать местные потери и по-прежнему исходить из общей формулы Лейбензона это уравнение можно представить в следующем виде:
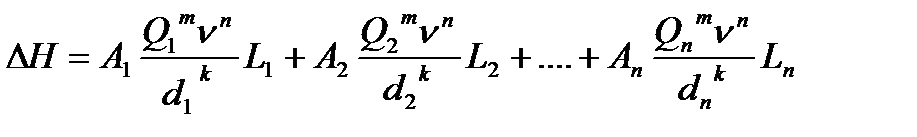 ,
,
Откуда, принимая во внимание, что в простом трубопроводе 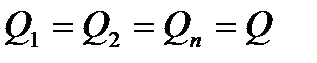 , находим
, находим 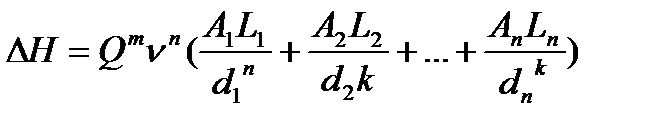 и легко определяем искомый расход жидкости
и легко определяем искомый расход жидкости
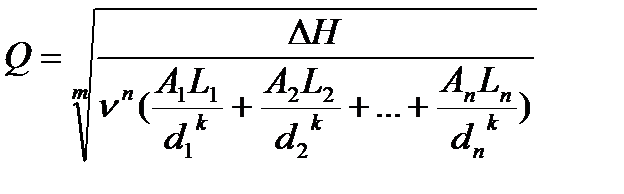 .
.
В случае квадратичного закона сопротивления, выполнив аналогичные преобразования, получим: 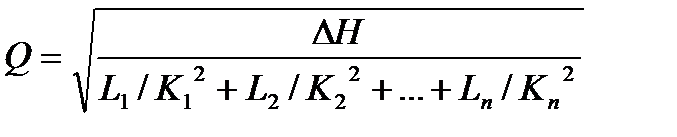 .
.
Дата добавления: 2016-06-15; просмотров: 1754;











