Вязкость стёкол и стеклообразующих расплавов

Вязкость стеклообразующих расплавов и стекломассы регулирует протекание протекания основных стадий технологического процесса: стеклообразования, гомогенизации и осветления стекломассы, формования изделий, их отжига или закалки и другие.

При движении потока жидкости, когда скорость течения различных слоёв потока неодинакова, в нём самопроизвольно происходят процессы, стремящиеся выровнять скорости течения слоёв. Эти процессы называются внутренним трением или вязкостью.

Динамическая вязкость η – физическая величина, равная отношению тангенциальной силы F_τ, необходимой для поддержания градиента скорости, равного единице, между двумя параллельными слоями жидкости, к площади соприкосновения этих слоёв. Динамическая вязкость η вводится как коэффициент пропорциональности уравнения:

F_τ = η 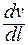Δs ,

η – динамическая вязкость;

F_τ – модуль силы внутреннего трения между смежными слоями жидкости;

dv/dl – модуль градиента скорости;

Δs – площадь соприкосновения слоёв жидкости.

Размерность и единица динамической вязкости:

[η] = 1 Н∙с/м² = 1Па∙с;

Паскаль-секунда равна динамической вязкости среды, касательное напряжение в которой при ламинарном течении и при разности скоростей слоёв, находящихся на расстоянии 1м по нормали к направлению скорости, равной 1м/с, равно 1Па.

В системе единиц СГС единица динамической вязкости 1 пуаз = 1П = 0,1 Па∙с. Следовательно, 1 Па∙с = 10 пуаз.

Текучесть – величина, обратная вязкости: φ = 1/ η.

Аналогично диффузионным процессам, при которых возникает поток вещества, стремящийся уменьшить градиент концентрации компонента (j = -D∙dC/dx), в процессах вязкого течения наблюдается поток импульса П, стремящийся уменьшить градиент скорости течения (П = - η∙ du/dx). Динамическая вязкость η характеризует быстроту передачи импульса из одного места потока в другое.

Наряду с динамической вязкостью часто рассматривают так называемую кинематическую вязкость. Поскольку скорость равна импульсу, делённому на массу, быстрота выравнивания скорости потока будет определяться отношением η/ρ, где ρ – плотность, т.е. масса единицы объёма жидкости. В связи с этим величину ν = η/ρ называют коэффициентом кинематической вязкости. Размерность кинематической вязкости [ν] = м²/с. В системе СГС единица измерения кинематической вязкости – стокс, размерность [ν] = см²/с. Размерность кинематической вязкости совпадает с размерностью коэффициента диффузии и, таким образом, кинематическая вязкость представляет собой как бы коэффициент диффузии для скорости потока.

Вязкость силикатных расплавов зависит от температуры: η = η(Т). При охлаждении расплава вязкость интенсивно нарастает. При температуре Т = 1500ºС вязкость стеклорасплава η = 10 Па∙с, при комнатной температуре вязкость стекла составляет η = 10¹⁹ Па∙с.

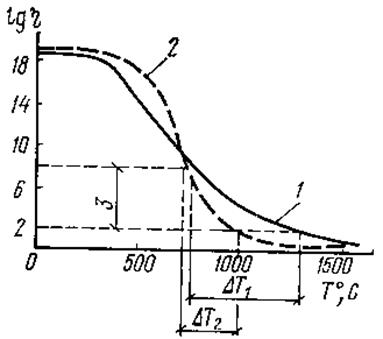
Температурный ход вязкости позволяет поделить силикатные стёкла на два класса: длинные и короткие (рис. 4.1).

Рис. 4.1. Температурный ход вязкости различных стёкол:

1 – длинное стекло; 2 – короткое стекло;

3 – вязкостный интервал формования;

ΔТ₁ и ΔТ₂ – температурные интервалы формования

соответственно длинного и короткого стекла

При повышении температуры от комнатной до температуры стеклования T_g вязкость меняется незначительно. Наиболее резко вязкость снижается в интервале 10¹⁵–10⁷ Па∙с.

Зависимость вязкости от температуры описывается уравнением Френкеля-Андраде:

,

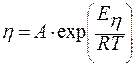где Е_η – энергия активации вязкого течения;

А – константа, зависящая от природы вещества.

Постоянная А рассчитывается по уравнению Эйнштейна:

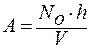; А = 10^-4–10^-5 Па∙с.

Уравнение справедливо для интервала температур, в котором не меняется степень ассоциации расплава, т.е. структурная единица вязкого течения остается постоянной.

Для силикатных стёкол энергия активации вязкого течения Е_η= 80–630 кДж/моль. Для металлов Е_η = 2–8 кДж/моль.

Если допустить, что при вязком течении скорость перетекания силикатного расплава регулируется движением тетраэдров SiO₄, то энергию активации вязкого течения расплава кварцевого стекла можно оценить как четыре энергии связи атома кремния с атомом кислорода Si–O: Е_Si–O= 1624 кДж/моль. Принятое приближение предполагает, что при смещении тетраэдра разрываются связи его мостиковых кислородов с окружением. Экспериментальная оценка показывает, что для чистого кварцевого стекла энергия активации вязкого течения намного меньше: Е_η = 630 кДж/моль.

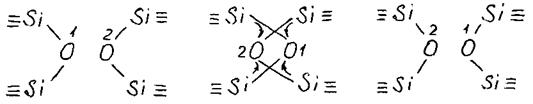
Для объяснения этого противоречия Мюллер предположил, что при вязком течении в силикатных расплавах связи не рвутся, а переключаются.

сближение переключение разведение

Маккензи считает, что единицей вязкого течения являются молекулы SiO₂. Эти молекулы выступают как промежуточная форма диоксида кремния при перемещении слоёв расплава.

O^- O^-

| |

O^- – Si – O^- → O = Si = O → O^- – Si – O^-

| |

O^- O^-

В многокомпонентных системах структурной единицей вязкого течения может быть мостиковый кислород, а в системе FeO–SiO₂ – анион кислорода O^2-.

Энергия активации вязкого течения складывается из энергии образования полости (дырки) по размерам, соответствующим структурной единице вязкого течения, а также из работы на перемещение этой частицы в образовавшуюся полость.

Работа на образование сферической полости рассчитывается по формуле:

,

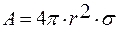где σ — поверхностное натяжение расплава стекла;

r — радиус перемещаемой частицы.

Допустим, что работа на смещение частицы (структурной единицы вязкого течения) намного меньше работы на образование полости. При этом условии энергия активации вязкого течения определяется работой образования поверхности полости в жидкости:

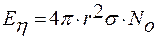– для 1 моля частиц,

где N_o – число Авагадро.

При Т > T_fвязкость рассчитывается:

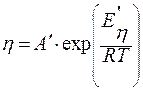
Если T < T_g, то 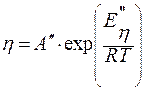, где .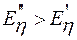

При условии выполнения уравнения Френкеля-Андраде энергию активации можно рассчитать, если известны значения динамической вязкости η при двух температурах:

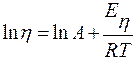или ;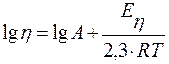

T₁: ;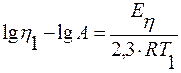

T₂: .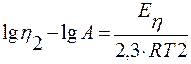

Вычтем из второго уравнения первое:

;

;

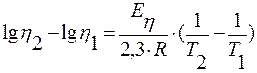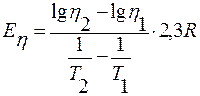При графической иллюстрации температурной зависимости вязкости в полулогарифмических координатах η = η(1/Т) для наглядности часто числитель и знаменатель дроби последнего уравнения представляют в виде отрезков а и b:

; ; ;

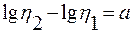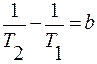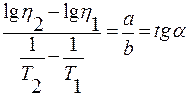E_η=2,3R∙tgα,

где α – угол наклона прямой η = η(1/Т) относительно оси абцисс.

При экспериментальном определении величины E_η по графику η = η(1/Т) типичной ошибкой является непосредственное измерение линейкой отрезков а и b или измерение угла α транспортиром, что подразумевает зависимость энергии активации от выбора масштаба рисунка. Отрезок а определяется по разности двух значений lgη, отрезок b – по разности обратных температур.

В интервале стеклования вязкость стекла не подчиняется уравнению Френкеля-Андраде. Энергия активации вязкого течения здесь зависит от температуры:

1. Т ↓ Е_η↓, так как увеличивается свободный объём жидкости;

2. Протекает процесс ассоциации-диссоциации оксидных группировок.

Допустим, что уменьшение энергии активации вязкого течения с температурой описывается обратной зависимостью. В этом приближении вязкость стекла в интервале стеклования подчиняется уравнению:

если 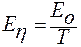, то ,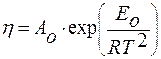

здесь А_о – постоянная;

Е_о – величина, пропорциональная прочности связи элемент–кислород.

В области высоких температур расплавы силикатных стёкол подчиняются закону Ньютона. Нормальные (ньютоновские) жидкости: коэффициент вязкости не зависит от действующей силы.

В интервале стеклования стекломасса является структурированной жидкостью. При приложении нагрузки нарушаются отдельные связи между частицами. Коэффициент вязкости здесь является функцией от действующей силы, а энергия активации различна для разных температур. Поэтому энергию активации вязкого течения определяют с использованием уравнения Френкеля-Андраде за пределами интервала стеклования.