Энергия Гиббса регулярного раствора

(реального раствора)

Регулярным называется раствор, удовлетворяющий следующим условиям:

1) размеры частиц практически одинаковы;

2) энергии взаимодействия между одноимёнными и разноимёнными частицами не равны: .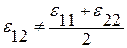

Требованиям регулярного раствора отвечает большой класс реальных растворов. Образование регулярного раствора сопровождается тепловым эффектом. Однако различие в энергиях связи должно быть небольшим, чтобы энергии теплового движения было достаточно для исключения какого-либо упорядочения частиц в растворе. Поскольку упорядоченности частиц нет, то изменение энтропии при смешении компонентов регулярного раствора находят так же, как для идеального раствора. Учтём тепловой эффект при образовании регулярного раствора.

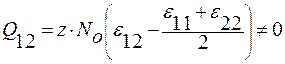; ΔH_р-р = Q₁₂∙N₁∙N₂ .

ΔG_р-р = ΔН_р-р – Т∙ΔS_р-р; ΔG_р-р = G_р-р – G_исх.

G_р-р = G_исх – Т∙ΔS_р-р + ΔН_р-р .

В соответствии с прежними обозначениями: G_р-р = а + b + c;

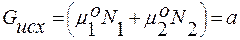– стандартные состояния компонентов регулярного и идеального растворов совпадают.

;

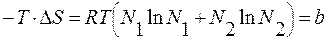ΔH_р-р = Q₁₂∙N₁∙N₂ = c.

Энергия Гиббса регулярного раствора составит:

.

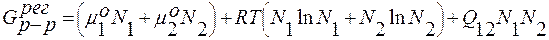В отличие от энергии Гиббса идеального раствора, появляется третье слагаемое, представляющее собой тепловой эффект ΔH_р-р при образовании реального раствора: Q₁₂∙N₁∙N₂ = c.

Выделяют два случая:

1. Q₁₂ < 0; c < 0; .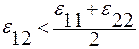

Связи в растворе слабее, чем в чистых компонентах (рис.3.30).

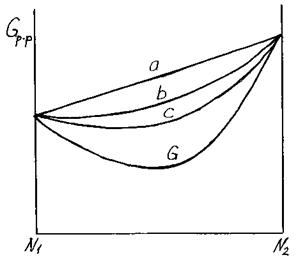
Рис. 3.30. Изменение энергии Гиббса при относительно

слабом взаимодействии разноимённых компонентов

Система устойчива, гомогенна, ликвация (фазовое разделение) невозможна. Имеем один минимум, устойчивому состоянию отвечает один раствор.

2. Q₁₂ > 0; c > 0; .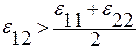

В растворе связи разноимённых частиц сильнее по сравнению с взаимодействием чистых компонентов. В расплаве возникают области, в которых преобладают разноимённые связи (рис. 3.31).

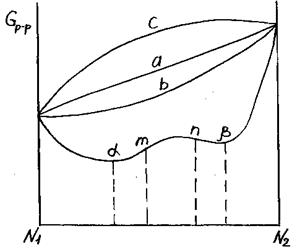
Рис. 3.31. Изменение энергии Гиббса раствора с составом при образовании прочных контактов разноимённых частиц

Термодинамически устойчивым состоянием в случае формирования в растворе связей более прочных, чем в чистых компонентах, оказывается фазовое разделение исходного расплава на две жидкости. Их составы определяются температурой и концентрацией исходного расплава. Исходная жидкость распадается на две жидкие фазы, обогащённые разными компонентами.

α и β – точки минимума, соответствующие равновесным составам фаз после ликвации.

m и n – точки перегиба линии зависимости G_р-ра =G_р-ра(N₂).

Критические параметры находятся из соотношений:

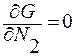– определяем координаты точек минимума α, β;

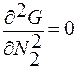– находим положение точек перегиба m, n.

Кривые G = G (N₂) строятся для разных температур и по положениям точек α и β находят область расслаивания (рис. 3.32).

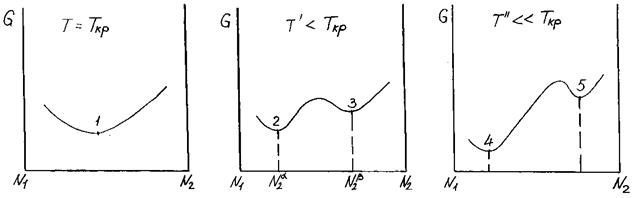
Рис. 3.32. Влияние температуры на зависимость энергии Гиббса от состава бинарного расплава

По полученным данным строим график зависимости T=T(N₂), называемый куполом ликвации (рис. 3.33).

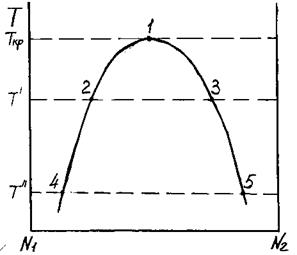
Рис. 3.33. Купол ликвации в двойной системе