Энергия Гиббса идеального раствора

Раствор называется идеальным, если:

1) размеры всех частиц одинаковы;

2) энергия взаимодействия одноименных и разноименных частиц совпадают.

ε₁₁ = ε₂₂ = ε₁₂; Q₁₂ = 0; ΔU = 0; ΔV = 0; ΔH = 0;

ΔG = ΔH – TΔS = – TΔS;

Изменение энергии Гиббса при образовании идеального раствора обусловлено только изменением энтропии.

Найдём изменение энтропии при образовании идеального раствора ΔS_{ид.р-ра.}

М₁ – число молекул первого компонента.

М₂ – число молекул второго компонента.

N_o – число Авагадро.

n₁ = M₁/N_о – число молей первого компонента.

n₂ = M₂/N_о – число молей второго компонента.

S₁^o и S₂^o – молярные энтропии чистых компонентов.

S_исх = n₁S₁^o + n₂S₂^o = k∙lnW_исх.

S_р-ра = n₁S₁^o + n₂S₂^o + ΔS_смеш = k∙lnW_р-ра.

S = k∙lnW; 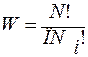; ΔS = ΔS_р-ра – ΔS_исх.

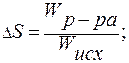
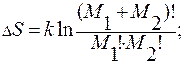
(М₁+М₂)! – общее число перестановок частиц. Делением на произведение М₁!∙М₂! исключаются перестановки одинаковых частиц.

Воспользуемся формулой Стирлинга (справедливой для больших чисел):

lnx! = x∙lnx – x.

;

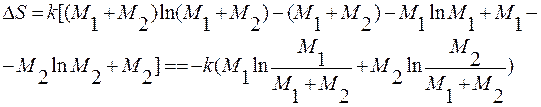М₁ = n₁∙N_o; М₂ = n₂∙N_o; n – число молей; k∙N_o = R;

; ;

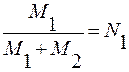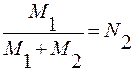ΔS = - R∙(n_l∙lnN₁ + n₂∙lnN₂);

ΔS > 0, так как N₁<1 и N₂<1;

S_р-ра = n₁S₁^o + n₂S₂^o - R∙(n_l∙lnN₁ + n₂∙lnN₂);

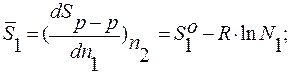
H_р-р = n₁H₁^o + n₂H₂^o ; ;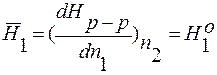

;

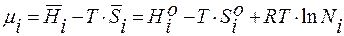Для идеального раствора: ;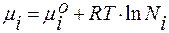

В общем случае:

; ;

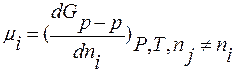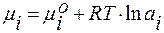Для идеального раствора активность компонента равна его мольной доле: a_i= N_i. Найдём энергию Гиббса идеального раствора:

G_p-p= μ₁∙N₁ + μ₂∙N₂ ;

; ;

;

;

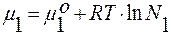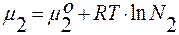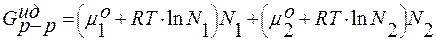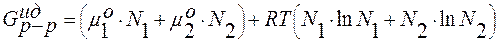Слагаемое 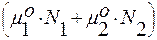= а – меняется линейно с составом раствора (рис. 3.29).

Слагаемое 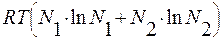= b < 0 и расположено, следовательно, ниже зависимости а = а (N₂).

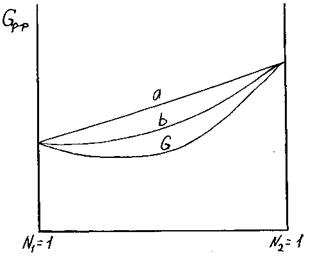
Рис. 3.29. Изменение с составом энергии Гиббса

идеального раствора

При образовании идеального раствора на зависимости G_p-p = f (N₂) выявляется один минимум, соответствующий устойчивому состоянию (или составу) системы. Поэтому ликвация – равновесное сосуществование двух различных растворов, в данном случае невозможна.