Комбинированные методы.

Эти методы используются для решения задач календарного планирования (теория расписаний). К ним примыкают эвристические методы, основанные на моделировании человеческого мышления.

Комбинированные методы делится на точные и приблизительные.

При использовании приближенных методов можно оценить степень приближения. Наиболее известный из этой группы методов, метод «ветвей и границ»: заключается в том, что все множество решений разбивается на ряд непересекающихся подмножеств и определяется их границы. Верхняя граница определяется при решении задач на max, нижняя на min.

При помощи этих определенных границ производиться дальнейшее деление на подмножества. Где-то в конце ветки находится оптимальное решение.

Метод случайного поиска: выбирается точка, далее используются датчики (генераторы) случайных чисел, мы начинаем двигаться от этой точки в определенном направлении. Из разделенного варианта направлений выбирается рациональный. Далее движение продолжается по этому выбранному рационал., при этом шаги движения удлиняются.

Задача о коммиваетере:

Объекты, которые должны посетить коммиваетер (при min расстояния, передвижений должно посетить лишь 1 раз каждый объект).

городов n, тогда число вариантов последовательного их посещения

(n-1)!

11 городов-10!=3628800

Сущность динамического программирования. Экономическая постановка и общий вид математической модели задач динамического программирования

Динамическое программирование используется для решения многошаговых экономических и технических задач, т.е. решение находится не для определения времени, а для многошагового процесса. Идея многошаговой оптимизации состоит в то, что оптимизируется на данном шаге на последующий шаг, т.е. используется системный подход.

Т.к. цель решения задачи достигается на конечном или последнем шаге и единственным этапом, который не влияет на последующий является последний шаг, то обычно задачи динамического программирования решаются от последнего этапа к первому, т.е. в обратном направлении.

Для каждого возможного итога на предпоследнем шаге находится оптимальное решение на последнем шаге.

Запишем формально гипотезы об исходе на предпоследнем шаге.

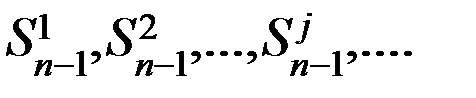- вариант результатов предпоследнего шага.

Тогда оптимальное решение на последнем шаге для каждой из гипотез рассчитывается:

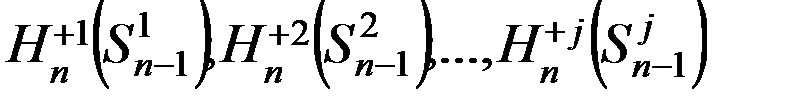
Такой алгоритм называется условным оптимальным управлением.

Затем осуществляется переход к оптимизации предпоследнего шага, при этом делятся ряд предположений о том, чем закончится n-2 шаг:

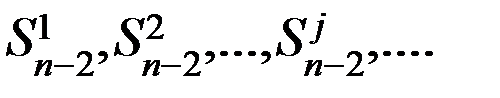
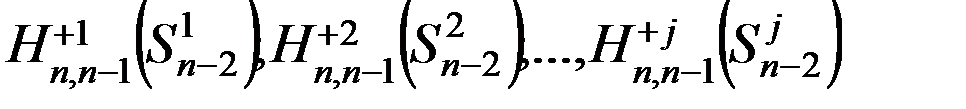
Здесь для исходя n-2 шага вме6сте оптимизируются (n-1) и n-й шаги и .т.д.

На каждом шаге мы отбрасываем множество заведомо неоптимальных решений.

Все динамическое программирование основывается на принципе оптимальности Беллмона: если в процессе решения оптимальный первый этап, то эта оптимизация является их главной частью, оптимизация процесса в целом. (Всякая часть оптимального пути оптимальна).