Модифицированный метод Ньютона.

Точность в определении корня также может быть повышена следующим образом. Воспользуемся формулой:

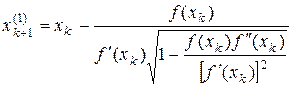. (2)

Вычисление корня итерационным методом с использованием формулы (2) называют модифицированным методом Ньютона.

В случае модифицированного метода Ньютона скорость сходимости на порядок выше, чем в методе Ньютона.

Если 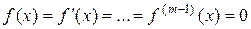, то говорят, что корень 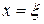имеет кратность т. Кратный корень уравнения может быть найден, если вместо исходного уравнения 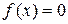метод Ньютона применить к уравнению 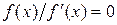, которое имеет тот же корень кратностью 1. После преобразований приходим к формуле

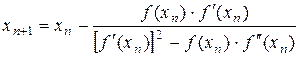. (3)

Формулу (3.11) рекомендуется применять при медленной сходимости метода Ньютона, когда есть подозрение на наличие кратного корня. В тех случаях, когда кратность корня заранее известна, он может быть найден по более простой итерационной формуле

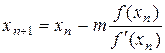, (4)

где т - кратность корня.

Формулы (1), (2), (3) и (4) могут быть использованы для вычисления как действительных, так и комплексных корней уравнений. В последнем случае начальное приближение корня является комплексным числом.

Выводы.

Сравнение методов численного решения уравнений, рассмотренных в вопрос е 2-3, с методом бисекций показывает гораздо более быструю сходимость метода Ньютона и его модификации. Это достигается за счёт использования свойств функции. Однако следует иметь в виду, что в методе Ньютона налагаются более жёсткие условия на функцию – требование дифференцируемости, сохранение знака f(x) и 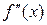в окрестности корня.