Условная вероятность. Теоремы сложения и умножения вероятности
Суммой (А+В) событий А и В называется событие, состоящее в появлении хотя бы одного из событий А или В.
Произведением (АВ) событий А и В называется событие, состоящее в появлении и события А, и события В.
Произведение несовместных событий А и В есть событие невозможное.
Для пары противоположных событий их произведение А 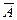 есть невозможное событие, а сумма А+
есть невозможное событие, а сумма А+ 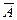 - событие достоверное.
- событие достоверное.
События А и В называются независимыми, если появление одного не влияет на вероятность появления другого.
Понятие независимости в теории вероятностей имеет более глубокий смысл, чем независимость обычная. Принято считать события независимыми, если они не связаны причинно. На практике, понятие зависимости и независимости случайных событий относительно. Если события слабо связаны, и эта связь несущественно влияет на конечный результат, то такие события считают независимыми, поскольку в этом случае построение математических моделей реальных ситуаций становится много проще. Наиболее глубоко в теории вероятностей изучены именно независимые события.
Если появление события А влияет на вероятность появления В, то вероятность Р(В|А) события В называется условной вероятностью при условии, что А произошло.
Пример 1. Орнитологи измеряют массу у двух из восьми особей, отбирая их произвольным образом. Какова вероятность того, что обе птицы будут окольцованы, если известно, что среди имеющихся восьми пять особей окольцованы?
Предполагаем, что для взвешивания птицы выбираются случайным образом по одной и после взвешивания отпускаются. Пусть событие А - первая взвешиваемая птица окольцована. Тогда Р(А)=5/8. Обозначим событие В - вторая взвешиваемая птица окольцована. Тогда вероятность события В приходится находить с учетом того, произошло событие А или нет. Если А произошло, т.е. уже одна окольцованная птица взвешена и отпущена, то Р(В)=4/7. Если А не произошло (опыт состоялся), то была выбрана для первого взвешивания птица без кольца и соответственно, Р(В)=5/7. Таким образом, события А и В зависимы, а вероятности В, которые были найдены являются условными вероятностями: 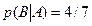 Р(В|А)=4/7,
Р(В|А)=4/7, 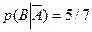 . Для ответа на поставленный вопрос требуется найти вероятность произведения событий А и В. Для этого можно применить следующий результат:
. Для ответа на поставленный вопрос требуется найти вероятность произведения событий А и В. Для этого можно применить следующий результат:
Теорема умножения вероятностей. Вероятность появления двух событий А и В равна произведению вероятности одного из событий на условную вероятность другого: Р(АВ)= Р(А)Р(В|А)=Р(В)Р(А|В).
Возвращаясь к задаче, вероятность взвесить двух окольцованных птиц: 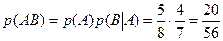 .
.
Теорема сложения вероятностей.Вероятность появления хотя бы одного события А или В равна сумме вероятностей этих событий без вероятности их совместного появления: Р(А+В)=Р(А)+Р(В)-Р(АВ).
Если события А и В несовместны, то Р(А+В)=Р(А)+Р(В).
Для нахождения вероятности суммы независимых событий А1, А2,…, Аn выгодно переходить к противоположным событиям:
Р(А1 +А2+…+Аn)=1-Р( 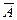 1)Р(
1)Р( 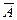 2)…Р(
2)…Р( 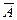 n).
n).
Пример 2. Вероятность того, что покупатель увидит рекламу продукта А по одному ТВ каналу 0,6. Реклама данного товара представлена на трех ТВ каналах. Какова вероятность, что покупатель не увидит рекламу данного товара ни по одному из них? Хотя бы по одному из трех каналов?
Решение. Пусть событие А –. покупатель не увидит рекламу данного товара ни по одному из трех каналов. Это событие является произведением следующих попарно независимых событий: А1 покупатель не увидит рекламу данного товара попервому каналу; А2– покупатель не увидит рекламу данного товара по второму каналу; А3 – покупатель не увидит рекламу данного товара по третьему каналу. Вероятность каждого из этих событий равна 0,4. По теореме умножения вероятностей имеем: Р(А) = (0,4)3= 0,064.
Пусть событие В –. покупатель увидит рекламу данного товара хотя бы по одному из трех каналов Это событие является суммой следующих совместных событий: В1 - покупатель увидит рекламу данного товара по первому; В2– покупатель увидит рекламу данного товара по второму каналу; В3 – покупатель увидит рекламу данного товара по третьему каналу. Удобнее перейти к противоположному событию, вероятность которого найдена выше Р(В1 +В2+В3)=1- (0,4)3 =1-0,064=0,936.
Дата добавления: 2018-11-26; просмотров: 914;











