Понятие случайного события. Классическое определение вероятности

12 3 4

Случайное событие – одно из первичных в теории вероятностей. При формальном аксиоматическом построении теории вероятностей случайное событие рассматривается как неопределяемое понятие, свойства которого раскрываются в системе аксиом.

Случайные события не существуют сами по себе, они возникают как результат некоторого действия, опыта, наблюдения. Будем использовать чаще всего термин «опыт». Любой опыт характеризуется определенной совокупностью условий, при которых он осуществляется. Например, измерение массы предмета - опыт, который проводится определенным прибором, с выбранной точностью измерения, при определенных физических параметрах окружающей среды и т.п.

Случайным событием называют любой факт, который в результате опыта может произойти или не произойти.

Обозначать события будем буквами русского или латинского алфавита, например, А, В, С.

Пример 1. Опыт: измерение массы тела человека.

Случайные события, связанные с данным опытом: А - «масса превышает допустимые нормы», В – «масса в пределах физиологических норм», С «масса превышает 50 кг»

Пример 2. Опыт: однократный бросок игральной кости (кубика).

Случайные события: А - «выпадение 1 очка», В – «выпадение 2 очков», С – «выпадение четного числа очков», Е - «выпадение нечетного числа очков», F – «выпадение числа очков, большего 4 » и т.д.

Из примеров следует, что случайные события не существуют в единственном числе, у каждого из них должно быть, по меньшей мере, альтернативное событие. Можно сказать, что под случайнымипонимаются наблюдаемые события, каждое из которых обладает возможностью реализоваться в данном опыте.

Если в результате опыта обязательно должно произойти одно и только одно из нескольких событий А_1,А_{2 ,}А_n, то говорят, что данные события образуют полную группу (систему) событий.

Пример 3. При бросании игрального кубика можно определить полную группу, состоящую из следующих событий: «выпадение одного очка», «выпадение двух очков», «выпадение трех очков», «выпадение четырех очков», «выпадение пяти очков», «выпадение шести очков».

Но, для этого же опыта можно выделить и другие полные группы событий. Например: «выпадение четного числа очков» и «выпадение нечетного числа очков».

В этом примере важно увидеть и еще один важный момент: любой бросок кубика дает конкретное число очков, поэтому группа событий, приведенная первой для этого опыта, состоит из конкретных результатов (исходов) этого опыта. Во втором варианте случайные события наступают при появлении одного из возможных результатов опыта. Выпало два очка, или четыре, или шесть – любой из этих вариантов приводит к наступлению случайного события «выпало четное число очков». В этом случае приведенные исходы опыта являются благоприятными для наступления данного события.

Важно уметь сравнивать события по степени возможности их наступления, а также правильно анализировать отношения между событиями, возникающими в одном опыте.

Достоверным событиемназывают такое событие,которое обязательно произойдет при осуществлении данного опыта, т.е. любой исход опыта для него -благоприятный. Обозначается достоверное событие - D .

Невозможным событиемназывают событие, которое никогда не происходит при осуществлении данного опыта, т.е. ни один из исходов опыта не будет для этого события благоприятным. Обозначается невозможное событие - N.

События А_1,А_{2 ,}А_n , которые в результате опыта вместе произойти не могут, называют несовместными (несовместимыми) в данной совокупности. Если в одном опыте возможно появление А_1,А_{2 ,}А_n, то данные события совместны в этой совокупности. События, образующие полную группу событий, несовместны ни в какой совокупности.

Два единственно возможных и несовместных события называются противоположными по отношению друг к другу. Для события А противоположное событие обозначается .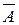

Количественная мера возможности наступления случайного события A в результате испытаний при заданной совокупности условий, выраженная числом, называется вероятностью этого события. Вероятность события обозначается обычно P(A). Это качественное определение нельзя считать математическим.

Существуют различные математические определения вероятности, они определяют вероятность количественно.

Классическое определение вероятности события.Пусть опыт имеет n равновозможных исходов, образующих полную группу событий, среди которых m исходов благоприятны для наступления события А, тогда вероятность А есть число .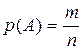

Классическое определение применяется только при выполнении условий: число исходов опыта конечно; исходы опыта равновозможны и образуют полную группу событий.

В других случаях формула классической вероятности не применима.

Из данной формулы легко получить следующие утверждения.

12 3 4

Дата добавления: 2018-11-26; просмотров: 985;