Свойства вероятности
1. Вероятность достоверного события равна 1: 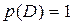
2. Вероятность невозможного события равна 0: 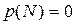
3. Для любого события выполняется равенство: 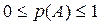 .
.
4. Для любого события: 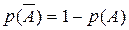 , где
, где 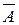 .- событие, противоположное А.
.- событие, противоположное А.
При решении задач на определение вероятности события полезно в анализе условий пользоваться следующей схемой:
1) Определить, в чем состоит опыт.
2) Что представляет собой элементарный исход опыта (элементарное событие пространства событий)?
3) Сколько равноправных исходов имеет опыт (сколько элементарных событий содержит пространство событий)? Если это число конечно - можно применять формулу классической вероятности.
4) В чем состоит событие, вероятность которого нужно найти?
5) Сколько благоприятных исходов для этого события имеет данный опыт?
6) Воспользоваться формулой классической вероятности.
Пример 5. Абонент забыл две последние цифры номера и набрал их наудачу, помня только, что эти цифры нечетные и разные. Найти вероятность того, что номер набран верно.
Решение. Опыт наудачу набирается две последние цифры номера.Различных исходов опыта столько, сколько существует двузначных чисел, записанных разными нечетными цифрами. Таких чисел 5×4 = 20 (используем комбинаторное правило произведения).
Событие А – абонент набрал верный номер. Из этих 20 возможных вариантов набора только один верный, следовательно, m=1, n=20 и 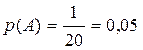 .
.
Ответ. Вероятность того, что номер набран верно, равна 0,05.
Отметим слабые стороны классического определения вероятностей. Классическое определение вероятности предполагает, что число элементарных исходов опыта конечно. На практике же часто встречаются испытания, число возможных исходов которых бесконечно или трудно подается учету. В классическом определении вероятности понятие равновозможны фактически означает равновероятны. Предполагается, что вероятность каждого элементарного исхода 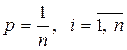 , что в реальных испытаниях не всегда выполнимо, т.е. вероятности элементарных исходов могут различаться.
, что в реальных испытаниях не всегда выполнимо, т.е. вероятности элементарных исходов могут различаться.
Поэтому наряду с классическим определением используют статистическое определение вероятности, основанное на понятии относительной частоты. Относительная частота есть отношение числа испытаний 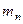 , в которых событие
, в которых событие  появилось к общему числу
появилось к общему числу  фактически произведенных испытаний:
фактически произведенных испытаний:
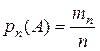 .
.
Основным свойством относительной частоты является ее устойчивость, которое состоит в том, что с ростом числа испытаний  относительная частота стабилизируется, колеблясь около постоянного числа
относительная частота стабилизируется, колеблясь около постоянного числа 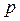 .
.
Статистическое определение вероятности. Предельное значение относительной частоты при неограниченном возрастании числа испытаний называют статистической вероятностью:
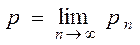 .
.
Дата добавления: 2018-11-26; просмотров: 899;











