Підходи до оцінки практичної стійкості симетричних криптоалгоритмів
Шифрування є одним з основних методів забезпечення конфіденційності даних в глобальних мережах, тобто захисту від несанкціонованого ознайомлення з ними. Згадаємо, що шифрування являє собою математичне перетворення 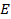 деякого конкретного вихідного набору даних
деякого конкретного вихідного набору даних 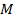 з множини усіх можливих
з множини усіх можливих 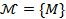 в зашифроване повідомлення
в зашифроване повідомлення 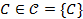 за допомогою секретного параметра – ключа зашифрування
за допомогою секретного параметра – ключа зашифрування 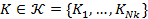 :
:
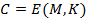 . (1)
. (1)
Звичайно, ключ зашифрування зв'язаний певним співвідношенням із ключем розшифрування; у цьому розділі будемо розглядати тільки алгоритми симетричного шифрування, у яких обидва ключі розшифрування та зашифрування для забезпечення безпеки даних згідно принципу Керкхофса зберігаються у таємниці.
Ступінь складності найкращого методу відновлення вихідних даних з зашифрованих та/або ключа шифрування (криптоаналітичної атаки) за умов застосування сучасних досягнень науки та техніки є однією з основних характеристик алгоритмів шифрування й називається його практичною криптостійкістю.
Криптографічна стійкість є кількісною характеристикою алгоритму шифрування, оскільки для розкриття конкретного алгоритму за певних умов потрібні певні ресурси, зокрема, ресурсами в цьому випадку є наступні величини:
1. Обсяг даних, що необхідні для здійснення атаки. Зокрема, це може бути мінімальна довжина шифрованого повідомлення або необхідна для реалізації атаки кількість відомих пар відкритих та відповідних їм шифрованих текстів.
2. Припустимий (максимальний) час  для реалізації атаки. Звичайно ця характеристика розраховується виходячи з потужності застосованої обчислювальної техніки (кількості елементарних операцій за секунду –
для реалізації атаки. Звичайно ця характеристика розраховується виходячи з потужності застосованої обчислювальної техніки (кількості елементарних операцій за секунду – 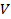 ) та кількості операцій
) та кількості операцій 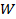 , що передбачені алгоритмом атаки, виконання яких при дотриманні інших необхідних умов дозволяє розкрити вихідний текст або обчислити ключ шифрування:
, що передбачені алгоритмом атаки, виконання яких при дотриманні інших необхідних умов дозволяє розкрити вихідний текст або обчислити ключ шифрування: 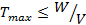 .
.
3. Обсяг пам'яті, що необхідний для зберігання використовуваної при атаці інформації, оскільки атака може висувати до неї досить істотні вимоги.
Сукупність цих трьох величин характеризує конкретну атаку на конкретний алгоритм шифрування. А краща (потребуюча мінімального набору ресурсів) з можливих атак на алгоритм характеризує його криптостійкість.
Існує й ще одна немаловажна характеристика алгоритму шифрування – наскільки шифротексти, що отримані з його допомогою, відрізняються від випадкової послідовності. Причому, дана характеристика може бути виражена кількісно в тих же трьох описаних вище типах ресурсів.
Звичайно, аналіз криптографічної стійкості алгоритму виходить з його повної та правильної реалізації, як це передбачено класом В3 безпеки засобів КЗІ. У той же час, у ході проведення інженерно-криптографічного аналізу засобів КЗІ, для оцінки наслідків відмови апаратних засобів виникає задача дослідження не повністю реалізованого або модифікованого алгоритму. Ця задача також виникає, у разі необхідності порівняння властивостей декількох стійких алгоритмів шифрування, як це відбувалося на конкурсі з вибору нового стандарту шифрування США ‑ AES.
У зазначених випадках використовується ще одна характеристика криптографічного алгоритму – запас криптостійкості (security margin).
Зокрема, відомо, що переважна більшість блокових криптоалгоритмів складається з певної кількості практично однакових або подібних циклів (раундів), у кожному з яких забезпечується процедури розсіювання та перемішування, внаслідок чого забезпечуються залежність кожного біту блоку даних, що шифрується, від кожного біту ключу та від усіх бітів відкритого блоку. При цьому з кожним циклом проміжне значення блоку за статистичними критеріями все більше наближається до випадкового та менше корелюється з початковим блоком. Після виконання усіх передбачених специфікацією стійкого алгоритму циклів неможливо за допомогою статистичних тестів відрізнити зашифровані блоки від суто випадкових, а також виявити їх кореляцію з відкритим блоком та ключем.
З метою визначення запасу криптостійкості можуть відбуватися дослідження модифікацій алгоритму зі зменшеним числом циклів. У цьому випадку запас криптостійкості оцінюється як співвідношення початкового (стандартного) числа циклів досліджуваного алгоритму та мінімальної кількості циклів його модифікації, що залишається криптографічно стійкою.
Інший спосіб визначення запасу криптостійкості – аналіз модифікацій досліджуваного алгоритму з незначними змінами структури циклу. Одним з показових прикладів цього підходу є метод розкриття ключу алгоритму Skіpjack-3XOR, який відрізняється від досить розповсюдженого алгоритму шифрування Skіpjack тим, що зі структури останнього вилучені всього 3 конкретні операції XOR (побітова логічна операція "виключне або") з передбачених у алгоритмомі Skіpjack 320 подібних операцій.
Складність згаданого методу за наявності 29 обраних пар відкритих текстів і відповідних їм шифротекстів оцінюється величиною біля 106 тестових операцій шифрування.
По сучасних мірках, завдяки даній атаці алгоритм Skіpjack-3XOR можна вважати досить слабким, що свідчить про можливо недостатній запас криптостійкості алгоритму Skipjack. Втім, у випадку інженерно-криптографічного аналізу реалізацій подібних алгоритмів дослідження запасу криптостійкості їх модифікацій доцільно розглядати як якісну характеристику, що має відношення до поведінки досліджуваного алгоритму в умовах випадкових загроз відмов обладнання (клас безпеки засобів КЗІ ‑ В2) або навмисного втручання у роботу засобу КЗІ (класи –В1 або Б2).
У загальному випадку, розкриття ключу є істотно більш складним, чим відновлення повідомлення. Водночас, отримав ключ шифрування, криптоаналітик може згодом розшифровувати всі дані, що зашифровані знайденим ключем. Така атака, у випадку її успішної реалізації, називається повним розкриттям алгоритму шифрування.
I. Огляд атак на алгоритми шифрування доцільно розпочати з методу повного перебору варіантів ключів абометоду грубої сили(brute force attack), що припускає можливість перебору за допомогою обчислювальної (у тому числі спеціально створеної для цього) техніки всіх припустимих варіантів ключів до знаходження істинного ключа шифрування.
В разі використання ключа шифрування у вигляді двійкового вектору довжиною 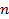 біт існує всього
біт існує всього 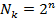 його різних варіантів. Найбільш просто цей метод реалізується у випадку наявності пари
його різних варіантів. Найбільш просто цей метод реалізується у випадку наявності пари 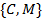 ‑ шифрований та відповідний йому відкритий текст. Впорядкував ключі в вигляді послідовності їх десяткових еквівалентів, атакуюча сторона здійснює поступове розшифрування за допомогою ключів:
‑ шифрований та відповідний йому відкритий текст. Впорядкував ключі в вигляді послідовності їх десяткових еквівалентів, атакуюча сторона здійснює поступове розшифрування за допомогою ключів:
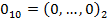 ,
, 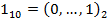 , … ,
, … , 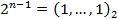 . (2)
. (2)
Якщо варіант вихідного тексту 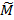 , що отриманий на черговому кроці методу у підсумку тестового розшифрування збігається з еталонним відкритим текстом
, що отриманий на черговому кроці методу у підсумку тестового розшифрування збігається з еталонним відкритим текстом 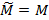 , то відповідний ключ може бути істинним. Справа у тому, що у разі недостатньої довжини шифрованого повідомлення розшифрування буде неоднозначним, кандидатів на істинний варіант буде декілька.
, то відповідний ключ може бути істинним. Справа у тому, що у разі недостатньої довжини шифрованого повідомлення розшифрування буде неоднозначним, кандидатів на істинний варіант буде декілька.
Мінімальна довжина шифрованого повідомлення, для якого розшифрування буде однозначним, отримала назву відстань єдиності. В теорії інформації відстань єдиності розраховується виходячи з надлишковості мови – її властивості, що характеризує передбачуваність чергового символу (букви) відкритого повідомлення за умов наявності декількох попередніх. Відстань єдиності, для європейських мов становить від 27 до 37 букв. Це означає, що у випадку меншої довжини «еталону» існує ненульова ймовірність помилки ‑ випадкового збігу, яка досить швидко зменшується у випадку збільшення довжини «еталона».
Звернемо увагу на те, що в цьому методі серед усіх отриманих варіантів ключу обов’язково буде істинний. Також відмітимо, що ключ може бути знайдений навіть після першого тестового розшифрування, у найгіршому випадку ключ буде знайдений тільки на останньому кроці Оцінімо обчислювальну складність методу, для цього знайдемо середню кількість кроків (тестових операцій розшифрування) до знаходження першого варіанту ключа (єдиного, у разі довжини відкритого повідомлення що перевищує відстань єдиності).
Вважаємо, що усі ключі застосовуються випадково та рівномірно з ймовірністю  , тоді на будь якому тестуванні (першому, другому, третьому тощо) ключ буде знайдений з цією ймовірністю. Користуючись формулою для суми членів арифметичної прогресії, розрахуємо середню кількість тестових випробувань
, тоді на будь якому тестуванні (першому, другому, третьому тощо) ключ буде знайдений з цією ймовірністю. Користуючись формулою для суми членів арифметичної прогресії, розрахуємо середню кількість тестових випробувань 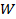 для цього методу:
для цього методу:
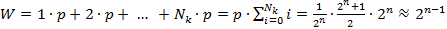 .
.
Наразі, з урахуванням числа 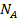 ‑ кількості операцій, що необхідні для реалізації процедури розшифрування тестовим ключем ‑ складність методу становить:
‑ кількості операцій, що необхідні для реалізації процедури розшифрування тестовим ключем ‑ складність методу становить:
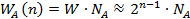 .
.
Захист від атак методом грубої сили досить простий – збільшення розміру ключа.
Ефективність атак за цім методом може бути підвищена за рахунок наступних технологій (припустимо одночасне застосування):
‑ попередньої вибраковки аналітичними методами певних варіантів ключів, наприклад методами диференціального або лінійного аналізу про які мова нижче;
‑ паралельного (одночасного) обчислення істинного ключу на декількох комп'ютерах, які виконують завдання пошуку у виділеній множині меншого об’єму;
‑ застосування спеціалізованих обчислювальних засобів для перевірки ключів для конкретного криптографічного алгоритму. Наприклад, побудований на основі програмованих логічних схем модуль ORCA (компанія AT&T) забезпечував перевірку 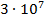 ключів алгоритму DES за секунду. В 1993 році Майкл Вінер (Mіchael Wiener) розробив принципи конструкції спеціалізованого комп'ютера вартістю порядку $1 000 000, здатного перебрати ключі DES за 3,5 години.
ключів алгоритму DES за секунду. В 1993 році Майкл Вінер (Mіchael Wiener) розробив принципи конструкції спеціалізованого комп'ютера вартістю порядку $1 000 000, здатного перебрати ключі DES за 3,5 години.
У сучасних умовах безпечною з точки зори атаки повного перебору ключів вважається довжина ключа від 80 біт, на довгострокову перспективу доцільно розглядати застосування ключу довжиною від 128 біт.
II. З урахуванням вже викладеного, можливо уточнити раніше дане визначення практичної стійкості, а саме, алгоритм шифрування вважається практично стійким, якщо у визначеній перспективі він не може бути розкритий за допомогою методу повного перебору ключів та не існує більш ефективного методу його дешифрування.
Ефективніший метод дешифрування ніж повний перебір ключів звичайно використовує певні недоліки побудови алгоритму або його реалізації у засобі КЗІ. Зокрема, метод атаки, що отримав умовну назву «зустріч посередині» (meet in the middle) базується на вразливості повторного використання блокового алгоритму:
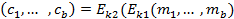 ,
,
де 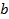 – довжина блоку,
– довжина блоку, 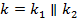 – об’єднаний ключ. Нескладно бачити, що довжина ключу у цьому випадку подвоюється, а загальна кількість різних ключів становитиме величину
– об’єднаний ключ. Нескладно бачити, що довжина ключу у цьому випадку подвоюється, а загальна кількість різних ключів становитиме величину 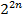 .
.
Атака "зустріч посередині" в застосуванні до алгоритму Double DES була запропонована Ральфом Мерклем (Ralph C.Merkle) і Мартіном Хеллманом (Martіn E.Hellman). Можливість застосування атаки вивчалася також щодо одного з варіантів "потрійного" DES (Triple DES).
Рівняння криптографічного перетворення у випадку алгоритму Double DES, що реалізує подвійне шифрування за допомогою стандартного алгоритму DES з 56-бітним ключем, має наступний вигляд:
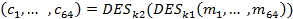 .
.
Раніше було відмічене, що довжина ключу стандартного алгоритму DES занадто мала, у той же час 112-бітний ключ алгоритму Double DES за методом повного перебору ключів в сучасних умовах практично неможливо розкрити ( 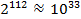 варіантів ключа).
варіантів ключа).
Ідея атаки «зустріч посередині» полягає у наступному. Припустимо, що є дві пари відкритих та відповідних їм шифрованих текстів (блоків) 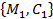 та
та 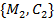 , які отримані за допомогою алгоритму Double DES з ключем
, які отримані за допомогою алгоритму Double DES з ключем 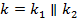 . Атака реалізується в два етапи: на першому за допомогою пари
. Атака реалізується в два етапи: на першому за допомогою пари 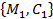 формується перевірочна таблиця та виконується відбір «кандидатів» на істинний ключ, на другому з використанням пари
формується перевірочна таблиця та виконується відбір «кандидатів» на істинний ключ, на другому з використанням пари 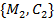 вибраковуються помилкові ключі. Загалом атаку описують наступні кроки:
вибраковуються помилкові ключі. Загалом атаку описують наступні кроки:
1. За допомогою кожного з ключів 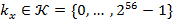 обчислюється результат – блок
обчислюється результат – блок 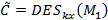 , що записується у перевірочну таблицю.
, що записується у перевірочну таблицю.
2. Для кожного ключу 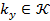 виконується розшифрування
виконується розшифрування 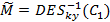 , після чого таблиці об’єднуються та впорядковуються, внаслідок чого співпадаючі блоки
, після чого таблиці об’єднуються та впорядковуються, внаслідок чого співпадаючі блоки 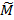 та
та 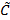 розташовуються разом.
розташовуються разом.
3. У разі збігу блоків 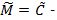 результатів, що отримані на кроках 1 та 2, відповідні ключі вважаються кандидатами на істинні ключі
результатів, що отримані на кроках 1 та 2, відповідні ключі вважаються кандидатами на істинні ключі 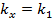 та
та 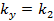 . Значна частина збігів буде випадковою, оскільки перевірці зазнає
. Значна частина збігів буде випадковою, оскільки перевірці зазнає 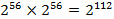 пар блоків. Ймовірність випадкового збігу двох блоків довжини 64 біт практично дорівнює
пар блоків. Ймовірність випадкового збігу двох блоків довжини 64 біт практично дорівнює 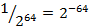 , тому середня кількість випадкових збігів буде досить значною:
, тому середня кількість випадкових збігів буде досить значною: 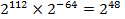 (варіантів помилкових ключів).
(варіантів помилкових ключів).
4. Для відбракування помилкових ключів використовується друга пара «відкритий-шифрований блок»: 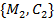 . З цією метою кожен «кандидат» в істинні ключі, який успішно протестований на кроці 3, використовується для шифрування блоку
. З цією метою кожен «кандидат» в істинні ключі, який успішно протестований на кроці 3, використовується для шифрування блоку 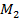 , результат чого порівнюється з блоком
, результат чого порівнюється з блоком 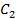 . При цьому ймовірність повторного випадкового збігу залишається достатньо малою:
. При цьому ймовірність повторного випадкового збігу залишається достатньо малою: 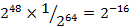 . За необхідності, має бути використана третя пара блоків
. За необхідності, має бути використана третя пара блоків 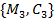 .
.
Таблиця 1
Складність атак за методом «зустріч посередині» (довжина ключу – n, довжина блоку ‑ b)
| №№ | Назва операції | Складність/кількість операцій |
| 1. | Зашифрування 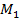 на усіх ключах на усіх ключах
| 
|
| 2. | Розшифрування 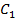 на усіх ключах, на усіх ключах,
| 
|
| 3. | Об’єднання таблиць в одну та її впорядкування | 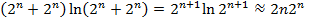
|
| 4. | Відбраковування помилкових варіантів | 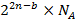
|
З таблиці 1 можливо бачити, що складність обчислення ключа Double DES даної атаки усього в 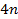 разів вище, ніж повний перебір ключів звичайного DES, що незрівнянно менше 2112 можливих варіантів "подвійного" ключа. Однак розв’язок задачі вимагає значного об’єму пам’яті ≈1017.
разів вище, ніж повний перебір ключів звичайного DES, що незрівнянно менше 2112 можливих варіантів "подвійного" ключа. Однак розв’язок задачі вимагає значного об’єму пам’яті ≈1017.
Метод "зустріч посередині" згодом неодноразово був використаний для аналізу проектів різних алгоритмів шифрування. Зокрема, під час проведення конкурсу AES досліджувалися алгоритм DEAL: 2166 тестових операцій шифрування обчислення 192-бітного або 2222 операції для обчислення 256-бітного ключа, алгоритм SAFER+: 2240 операцій шифрування для розкриття 256-бітного ключу.
Не зважаючи, що на відміну від Double DES, атака малоефективна проти сучасних алгоритмів шифрування, але її застосування може бути доречним під час оцінки запасу криптостійкості модифікованих версій алгоритмів.
III. Аналітичні методикриптоаналізу базуються на особливостях побудови функцій криптографічного перетворення 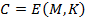 та можливості подання множини ключів
та можливості подання множини ключів 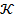 у вигляді прямого добуту множин:
у вигляді прямого добуту множин:
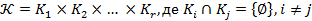 .
.
Нехай маємо відкрите 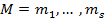 та шифроване повідомлення
та шифроване повідомлення 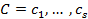 . В загальному випадку для перетворення
. В загальному випадку для перетворення  можна сформувати систему, яка буде описувати процес шифрування:
можна сформувати систему, яка буде описувати процес шифрування:
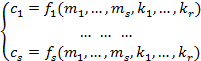 (3)
(3)
В системі рівнянь (3) невідомими параметрами залишаються тільки  .
.
Аналіз системи (3) може запропонувати більш швидкі методи її розв’язку, ніж повний перебір. Розглянемо декілька варіантів:
1.Припустимо, щосистема (3) може бути перетворена у “трикутниковий” вигляд:
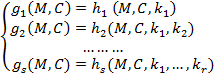 . (4)
. (4)
Будемо вважати, що розв’язок першого рівняння можна знайти тестуванням частини загального ключа 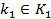 використовуючи перше рівняння в (4) для перевірки правильності розв’язку. Отримане значення використовується для розв’язку другого рівняння знову методом повного перебору, але стосовно другої частини загального ключу
використовуючи перше рівняння в (4) для перевірки правильності розв’язку. Отримане значення використовується для розв’язку другого рівняння знову методом повного перебору, але стосовно другої частини загального ключу 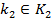 . Знайдене значення
. Знайдене значення 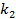 підставляємо в третє рівняння і так далі.
підставляємо в третє рівняння і так далі.
В результаті отримуємо загальний ключ:
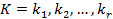 ,
,
виконав не більше ніж 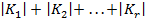 опробувань. Це число, звичайно, значно менше ніж кількість операцій методу грубої сили
опробувань. Це число, звичайно, значно менше ніж кількість операцій методу грубої сили 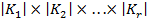 .
.
2. Можливість виділення в системі (3) деяким способом підсистеми лінійних рівнянь призводить до суттєвого спрощення задачі криптоаналізу, оскільки у цьому випадку існує можливість застосування відомих методів розв’язку систем лінійних рівнянь складність яких суттєво менше переборних методів.
Нехай, в системі (3) може бути відокремлена підсистема лінійних рівнянь:
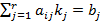 , (5)
, (5)
де параметри 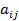 та
та 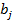 визначаються конкретними значеннями
визначаються конкретними значеннями 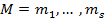 та
та 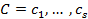 .
.
Для простоти розгляду вважаємо, що застосовується двійковий ключ та 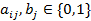 . Оцінімо складність находження ключу за методом Гаусса розв’язку сумісних систем лінійних рівнянь з r невідомими.
. Оцінімо складність находження ключу за методом Гаусса розв’язку сумісних систем лінійних рівнянь з r невідомими.
Як відомо, рішення системи (5) за методом Гаусса передбачає приведення розширеної матриці системи до діагонального вигляду. При цьому на першому кроці за допомогою небільше  операцій знаходиться рівняння у якому коефіцієнт при першому невідомому відрізняється від нуля
операцій знаходиться рівняння у якому коефіцієнт при першому невідомому відрізняється від нуля 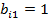 , після чого це рівняння віднімається з інших за допомогою не більше
, після чого це рівняння віднімається з інших за допомогою не більше 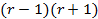 операцій. Таким чином, складність першого кроку не перевищує
операцій. Таким чином, складність першого кроку не перевищує 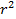 операцій.
операцій.
На другому кроці розглядається підсистема з 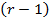 рівняння (за винятком рівняння, у якому
рівняння (за винятком рівняння, у якому 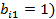 . За допомогою не більше
. За допомогою не більше 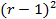 операцій повторюється процедура першого кроку і так надалі, поки на останньому кроці залишиться лише одна невідома змінна, значення якої використовується для знаходження попередньої, знайдених двох для третьої і так до кінця алгоритму.
операцій повторюється процедура першого кроку і так надалі, поки на останньому кроці залишиться лише одна невідома змінна, значення якої використовується для знаходження попередньої, знайдених двох для третьої і так до кінця алгоритму.
Наразі, оцінка складності методу 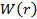 обчислюється наступним шляхом:
обчислюється наступним шляхом:
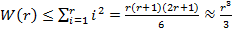 .
.
Не складно бачити, що складність за цим методом у випадку зростання довжини бітового ключу 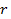 суттєво нижче, ніж у випадку методу повного перебору варіантів ключів:
суттєво нижче, ніж у випадку методу повного перебору варіантів ключів:
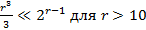 .
.
Існує ще декілька варіантів застосування аналітичних методів, які залежать від особливостей побудови криптографічних алгоритмів, але їх розгляд виходить за рамки курсу.
IV.Методдиференціального криптоаналізу вперше був запропонований Елі Біхамом (Elі Bіham) та Еді Шаміром (Adі Shamіr) для оцінки стійкості алгоритму блокового шифрування DES.
Для з’ясування особливостей цього методу криптоаналізу згадаємо принципи побудови та функціонування алгоритму DES. За допомогою алгоритму DES (рис. 3) інформація шифрується блоками по 64 біта з 56 бітним ключем.
Спочатку над 64-х бітний блок даних перетворюється первинна фіксована перестановка. Використані в стандарті DES таблиці замін та перестановок не приводяться через їхню громіздкість.
Після чого одержаний блок даних ділиться на два підблока по 32 біта кожен, початкові значення яких позначаються 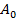 і
і 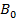 . Вказані підблоки зазнають 16 раундів перетворень відповідно до системи рівнянь:
. Вказані підблоки зазнають 16 раундів перетворень відповідно до системи рівнянь:
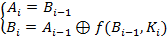 ,
,
де 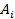 та
та 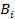 ‑ лівий та правий підблоки після виконання і-го раунду,
‑ лівий та правий підблоки після виконання і-го раунду, 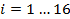 ,
,
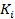 ‑ ключ і-го раунду, що формується з розширеного ключу,
‑ ключ і-го раунду, що формується з розширеного ключу,
Å - побітова логічна операція "виключне або" (XOR).
Значення функції 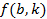 обчислюється наступним шляхом:
обчислюється наступним шляхом:
1. 32-х бітний вхідний підблок b за допомогою розширювальної перестановки EP перетворюється у 48-бітний блок be.
2. За допомогою операції XOR до блоку be додається ключ раунду Kі, позначимо результат цієї операції як bk:
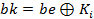
3. Отриманий результат bk розбивається на 8 фрагментів по 6 біт, кожен з яких перетворюється за допомогою відповідної таблиці замін (S1 ... S8) – так званих S ‑ блоків. Кожна таблиця містить по 4 рядки, що містять по 16 значень від 0 до 15. Вхідне значення інтерпретується в такий спосіб: два крайніх біти фрагмента формують номер рядка (від 0 до 3), з якого вибирається число, розташоване в стовпці, номер якого відповідає значенню чотирьох інших біт входу. Наприклад, при двійковому вході 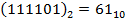 (десяткове число 61) вибирається значення сьомого елемента третього рядка відповідної таблиці.
(десяткове число 61) вибирається значення сьомого елемента третього рядка відповідної таблиці.
4. Отримані в результаті замін 4-бітні значення поєднуються в 32-бітний підблок bs, що перетворюється за допомогою ще одної перестановки ‑ P, чим завершується обчислення значення функції 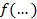 .
.
Після 16 раундів перетворень (останній раунд трохи відрізняється від попередніх ‑ у ньому підблоки не міняються місцями) виконується ще одна таблична перестановка, називана фінальною (рис. 3).
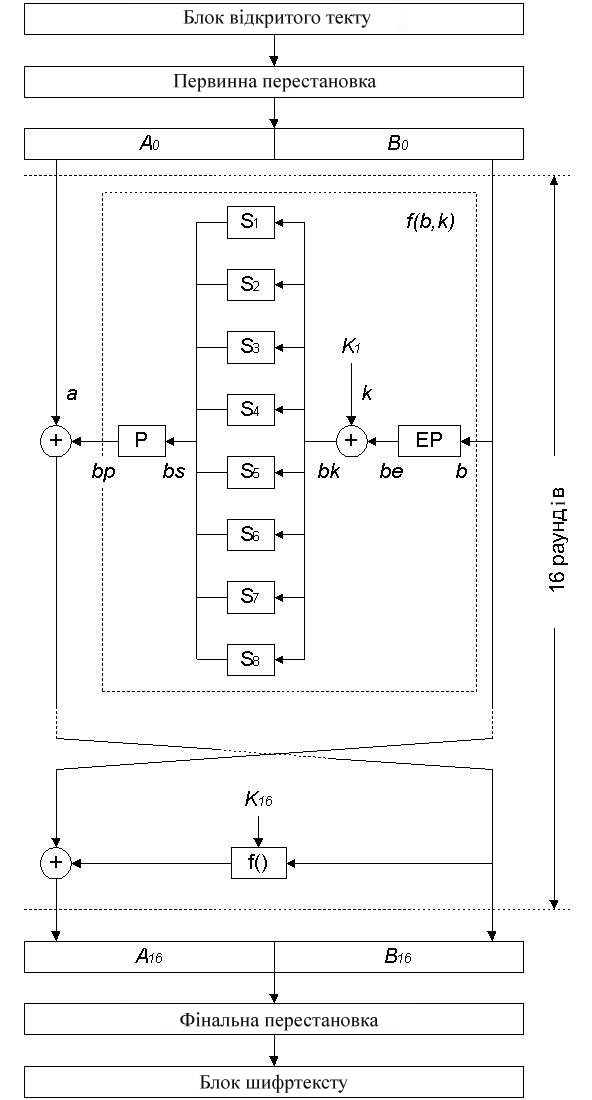
Рис.3. Структура алгоритму DES.
Схема процедури розширення ключа показана на рис. 4. Її завдання ‑ формування підключів для 16 раундів, що виконується в такий спосіб.
Спочатку, з 64-бітного ключа вибираються 56 значущий біт, які діляться на два 28-бітних фрагменти, які позначені як C і D.
Потім виконується 16 раундів процедури розширення ключа. Кожний раунд дає один з необхідних фрагментів Kі та складається з наступних перетворень:
1. Циклічний зсув поточних значень C і D вліво на один або два біт, залежно від номера раунду.
2. Поєднання отриманих C і D знов в 56-бітне значення, до якого застосовується стискаюча перестановка, результатом якої є 48-бітний ключ раунду Kі.
Слід звернути увагу, вказані перетворення у випадку фрагментів C і D, що цілком складаються з одиниць (нулів) породжують однакові ключі раундів: 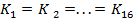 . Відповідні ключи отримали назву слабких.
. Відповідні ключи отримали назву слабких.
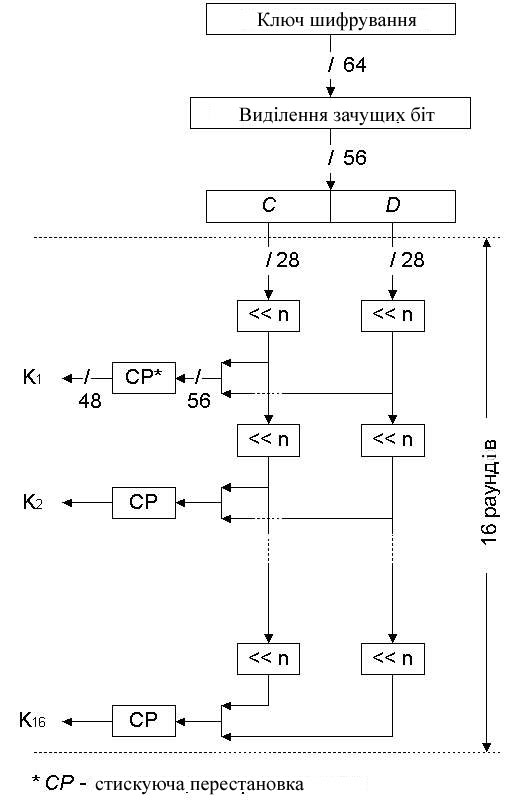
Рис.4. Процедура розширення ключа в алгоритмі DES.
При диференціальному криптоаналізі використовується деяка множину пар відкритих текстів, між якими існує певна різниця (difference). В випадку алгоритму DES різниця відкритих текстів M1 і M2 визначена як операція XOR між даними текстами:
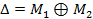 .
.
Аналіз пар текстів дозволяє виділити шуканий ключ (або його фрагмент), однозначно, або з найбільшої порівняно з іншими можливими ключами імовірністю.
Припустимо, є два блоки на вході функції 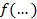 деякого раунду мають різницю Db:
деякого раунду мають різницю Db:
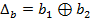 .
.
Нескладно, обчислити різницю 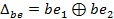 , після застосування до b1 і b2 розширювальної перестановки EP, оскільки:
, після застосування до b1 і b2 розширювальної перестановки EP, оскільки:
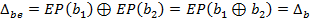 .
.
Наступна операція – додавання ключу раунду не змінює різницю:
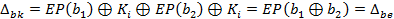 .
.
Аналогічно перетворенню EP, легко обчислити різницю Dbp після перестановки P:
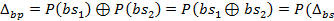 ).
).
Таким чином, лише таблична заміна як складова функції 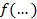 , істотно впливає на значення різниці. Значення
, істотно впливає на значення різниці. Значення 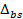 залежить не тільки від різниці
залежить не тільки від різниці 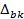 , але й від конкретних вхідних значень bk1 і bk2. Тут проявляється вплив доданого попередньою операцією ключа шифрування.
, але й від конкретних вхідних значень bk1 і bk2. Тут проявляється вплив доданого попередньою операцією ключа шифрування.
Таблиці замін міняють 6-бітне вхідне значення на 4-бітне. Це означає, що будь-якої вхідної різниці 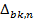 (де n ‑ номер таблиці) відповідає
(де n ‑ номер таблиці) відповідає 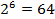 можливих пар вхідних значень, позначимо їх bk1,n і bk2,n. Відповідно, будь-якої вихідної різниці
можливих пар вхідних значень, позначимо їх bk1,n і bk2,n. Відповідно, будь-якої вихідної різниці 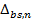 відповідає
відповідає 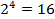 можливих пар
можливих пар 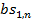 і
і 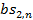 .
.
Диференціальний криптоаналіз алгоритму DES базується на тому, що, по-перше, кожне конкретне значення 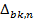 приводить не до всіх можливих 16 значень
приводить не до всіх можливих 16 значень 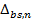 , а по-друге, ці значення
, а по-друге, ці значення 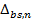 мають досить різну ймовірність. Бихам і Шамир, як приклад, проаналізували таблицю
мають досить різну ймовірність. Бихам і Шамир, як приклад, проаналізували таблицю 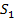 та її вхідну різницю
та її вхідну різницю 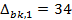 . Можливі значення різниці
. Можливі значення різниці 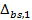 і відповідної ймовірності (для 64 можливих значень пари
і відповідної ймовірності (для 64 можливих значень пари 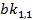 і
і 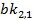 ) наведені в таблиці 2.
) наведені в таблиці 2.
Таблиця 2
Розподіл значень різниць для заміни 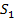
Значення 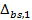
| D | F | Інші | ||||||
| Ймовірність | 8/64 | 16/64 | 6/64 | 2/64 | 12/64 | 6/64 | 8/64 | 6/64 |
Припустимо, що для шифрування використовувався однораундовий DES в розпорядженні криптоаналітика є пара текстів з 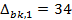 , а також відповідні їм шифротексти з
, а також відповідні їм шифротексти з 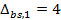 .
.
За таких умов, вхідні значення 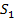 суть
суть 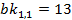 та
та 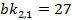 , або навпаки. Оскільки йому відомі відкриті тексти, то можна обчислити значення
, або навпаки. Оскільки йому відомі відкриті тексти, то можна обчислити значення 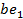 та
та 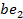 , а також два варіанти значень
, а також два варіанти значень 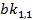 та
та 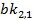 . За допомогою операції XOR обчислюється два можливих варіанти перших шести біт
. За допомогою операції XOR обчислюється два можливих варіанти перших шести біт  . Таким чином область можливих значень ключа звужується в
. Таким чином область можливих значень ключа звужується в 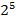 разів. За наявності, другої пари відкритих текстів з двох варіантів можливо обрати правильний.
разів. За наявності, другої пари відкритих текстів з двох варіантів можливо обрати правильний.
Для розкриття алгоритмів з більшим числом раундів необхідно використовувати такі різниці відкритих текстів, які з високою ймовірністю викликають певні різниці в одержуваних шифротекстах.
Прикладом застосування диференціального криптоаналізу є атака на відомий алгоритм RC2 за при наявності 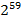 обраних відкритих текстів. Також відомим результатом є атака на широко використовуваний алгоритм RC5 (а саме, його основний варіант - RC5-32/12/16). Цей алгоритм є ще менш стійким по відношенню до диференціального криптоаналізу: він розкривається при наявності
обраних відкритих текстів. Також відомим результатом є атака на широко використовуваний алгоритм RC5 (а саме, його основний варіант - RC5-32/12/16). Цей алгоритм є ще менш стійким по відношенню до диференціального криптоаналізу: він розкривається при наявності 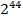 обраних відкритих текстів. Існують і інші варіанти алгоритму RC5, також піддані диференціальному криптоаналізу.
обраних відкритих текстів. Існують і інші варіанти алгоритму RC5, також піддані диференціальному криптоаналізу.
Підсумовуючи викладене слід зазначити, що метод диференціального криптоаналізу значною мірою є теоретичним підходом. Його практичне застосування обмежене суттєвими вимогами щодо обсягу вихідних даних. Ефективність методу суттєво залежить від структури S-блоків алгоритму, що досліджується. У той же час це є критерієм для вибору якісних блоків заміни, якщо стандарт алгоритму не встановлює їх конкретних значень.
Зважаючи на те, що атака за цим методом базується на обраних відкритих текстах, що потребує доступу до засобу КЗІ із завантаженим ключем, можливо зробити висновок, що диференціальний криптоаналіз складно реалізувати у випадку реальних криптосистем.
Усічені диференціали.При використанні диференціального криптоаналізу в ряді випадків, неможливо побудувати характеристику з досить високою ймовірністю, але можливо знайти таку характеристику, що використовує не цілком різницю між двома відкритими текстами або двома підблоками (відповідно, 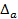 або
або 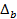 ), а якісь усічені диференціали (truncated differentials) – різницю між певними бітами оброблюваних даних. При цьому, імовірність таких характеристик може бути істотно вище, ніж імовірність класичних "повних" характеристик.
), а якісь усічені диференціали (truncated differentials) – різницю між певними бітами оброблюваних даних. При цьому, імовірність таких характеристик може бути істотно вище, ніж імовірність класичних "повних" характеристик.
Усічені диференціали можуть бути корисні, насамперед, при аналізі таких алгоритмів, у яких всі або майже всі операції виконуються над вирівняними фрагментами даних, наприклад, над байтами або 16-бітними словами. І навпаки, якщо алгоритм містить у достатній кількості які-небудь операції, що перемішують окремі біти даних, його можна апріорі вважати стійким проти усічених диференціалів.
Використання усічених диференціалів запропонував датський криптолог Ларс Кнудсен (Lars Knudsen). Він довів, що усічені диференціали більше ефективні в разі атаки на 6-раундовый DES, чим "класичний" диференціальний криптоаналіз. Однак, дану атака не була поширена на випадок DES з більшим числом раундів.
Згодом усічені диференціали були використані для побудови атак на відомі алгоритми Skipjack і SAFER. Результати аналогічні атакам на DES ‑ усічені диференціали виявилися максимально ефективні при атаках на варіанти алгоритмів з усіченим числом раундів, але їх не вдалося поширити на повнораундові версії алгоритмів.
Неможливі диференціали. Принципово новий варіант диференціального криптоаналізу, що використовує неможливі диференціали (іmpossіble dіfferentіals), був запропонований в 1998 році винахідниками диференціального криптоанализа Е. Біхамом та Е.Шамиром разом зі Алексом Бірюковим.
Якщо порівнювати неможливі диференціали із класичним диференціальним криптоаналізом, то видно, що використання неможливих диференціалів являє собою диференціальний криптоаналіз "від противного": даний метод використає диференціали з нульовою ймовірністю. Процес розкриття алгоритму за допомогою неможливих диференціалів можна коротко описати так:
1. Вибирається потрібна кількість пар відкритих текстів з необхідною різницею, отримують відповідні їм шифротексти.
2. Виконується аналіз отриманих даних, у рамках якого всі варіанти ключа шифрування, що приводять до неможливих диференціалів, вважаються помилковими й відкидаються.
3. У результаті залишається єдиний можливий варіант ключа або якась підмножина ключової безлічі, що не приводять до неможливих диференціалів; у випадку підмножини може бути використаний його повний перебір для знаходження вірного ключа.
Диференціали з нульовою ймовірністю можуть бути замінені диференціалами з мінімальною ймовірністю.
Неможливі диференціали були застосовані для розкриття усічених (по кількості раундів) версій таких відомих алгоритмів шифрування, як ІDEA, Skipjack, KASUMІ тощо.
V. Застосування лінійного криптоаналізудля розкриття алгоритмів блокового шифрування, а саме, алгоритму DESзапропоновано японським криптологом Міцуру Мацуі (Mіtsuru Matsuі). Зміст лінійного криптоаналізу блокового алгоритму полягає аналогічно системі (5) в знаходженні співвідношень наступного виду:
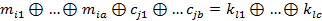 , (6)
, (6)
де 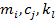 ‑ біти відкритого тексту, шифротексту та ключа відповідно. Такі рівняння називають лінійними апроксимаціями.
‑ біти відкритого тексту, шифротексту та ключа відповідно. Такі рівняння називають лінійними апроксимаціями.
Для довільно обраних біт відкритого тексту, шифротексту та ключа рівняння (6) виконується з ймовірністю 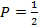 . У випадку знаходження таких біт, при яких імовірність P помітно відрізняється від
. У випадку знаходження таких біт, при яких імовірність P помітно відрізняється від  , даним співвідношенням можна скористатися для розкриття ключу алгоритму.
, даним співвідношенням можна скористатися для розкриття ключу алгоритму.
Так само, як і в диференціальному криптоаналізі, спочатку знаходиться деяке співвідношення для одного раунду, потім, за можливості, воно поширюється на більше число раундів, у результаті знаходиться співвідношення для повнораундового варіанту аналізованого алгоритму. Варто зазначити, що, на відміну від диференціального криптоаналізу, існують алгоритми пошуку співвідношень для повнораундового блокового алгоритму.
Найбільш ефективне рівняння для одного раунду алгоритму DES використовує ту властивість таблиці S5, що другий вхідний біт таблиці дорівнює результату додавання за модулем 2 його чотирьох вихідних біт з ймовірністю 3/16 (тобто менш на 5/16 порівняно з ймовірністю 1/2), тобто:
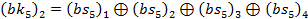 ,
,
що еквівалентно рівнянню:
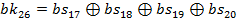 (7)
(7)
Далі, співвідношення (7) поширюється на раунд алгоритму в цілому, у результаті чого з урахуванням застосування перестановок виходить наступне співвідношення:
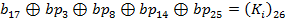 ,
,
де 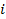 ‑ номер раунду. Отриманий результат поширюється на декілька раундів.
‑ номер раунду. Отриманий результат поширюється на декілька раундів.
З метою пошуку найбільш імовірних значень певних біт ключа шифрування з використанням максимально ефективного співвідношення виконується аналіз наявних пар "відкритий текст ‑ шифротекст".
Лінійний криптоаналіз може застосовуватися в сукупності з атакою методо
Дата добавления: 2016-06-15; просмотров: 2881;











