Дифференциальное уравнение равновесия жидкости
После рассмотрения некоторых частных случаев равновесия жидкости рассмотрим общее диф ференциальное равновесия в самом общем виде. Для этой цели выделим отсек жидкости малых размеров в виде параллелепипеда. Масса жидкости в выделенном объёме:
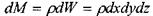
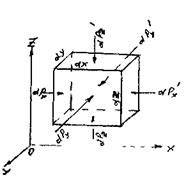
На боковые грани параллелепипеда действуют силы давления: (на левую и правую грани соответственно): 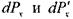 . На переднюю и заднюю грани:
. На переднюю и заднюю грани: 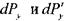 , на нижнюю и верхнюю грани:
, на нижнюю и верхнюю грани: 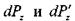
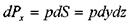
Поскольку давление на правую грань больше, то i 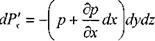
По аналогии можно записать силы давления на остальные пары граней.
на переднюю 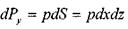 , на заднюю
, на заднюю 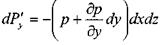 , на нижнюю
, на нижнюю
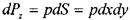 , на верхнюю
, на верхнюю 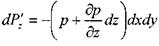 Проекции массовых сил на координатные оси:
Проекции массовых сил на координатные оси:
на ось ОХ будет на ось ОУ будет
на ось OZ будет 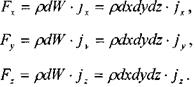 Тогда сумма сил действующих вдоль оси ОХ:
Тогда сумма сил действующих вдоль оси ОХ:
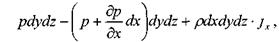
сумма сил действующих вдоль оси 07:
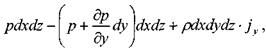
сумма сил действующих вдоль оси OZ:
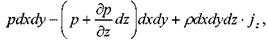
где: 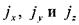 , проекции ускорения массовых сил на координатные оси.
, проекции ускорения массовых сил на координатные оси.
После преобразования получим систему дифференциальных уравнений равновесия жидкости:
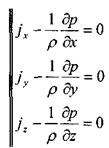 i i >
i i >
5.8. Сообщающиеся сосуды
В своей практической деятельности человек часто сталкивается с вопросами равновесия жидкости в сообщающихся сосудах, когда два сосуда А и В соединены между собой жёстко или гибким шлангом. Сами сосуды (А и В) обычно называются коленами. Такой гидравлический элемент часто используется в различных гидравлических машинах (гидравлические прессы и др.), системах гидропривода и гидроавтоматики, различных измерительных приборах и в ряде других случаев. С природ ными сообщающимися сосудами человек встречается с давних пор: сообщающимися сосудами больших размеров являются водонасыщенные пласты горных пород с системой колодцев, играющих роль отдельных колен природной гидродинамической системы.
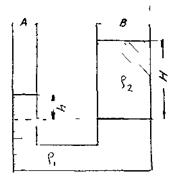
В открытых сообщающихся сосудах, заполненных однородной жидкостью свободный уровень жидкости устанавливается на одном и том же уровне в обоих коленах. Если в коленах сосудов залиты две несмешивающиеся жидкости с различной плотностью, то свободные уровни жидкости в правом и левом коленах устанавливаются на разных высотах в зависимости от соотношения плотностей жидкостей.
Для типичного случая, изображённого на рисунке, запишем уравнение равновесия жидкости относительно уровня раздела жидкостей.
или: 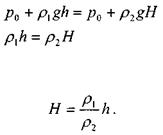
В закрытых сообщающихся сосудах давления на свободную поверхность могут быть шными, тогда уравнение равновесия будет иметь следующий вид:
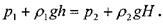
Дата добавления: 2016-06-09; просмотров: 1815;











