Сила давления жидкости па плоскую поверхность, погружённую в жидкость

Согласно основному закону гидростатики величина давления р определяется глу­биной погружения точки под уровень свободной поверхности h жидкости и величиной

плотности жидкости р.

Для горизонтальной поверхности величина давления одинакова во всех точках этой поверхно­сти, т.к.:

Отсюда: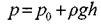

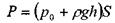
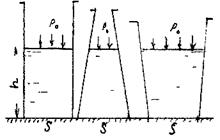
Таким образом, Сила давления жидкости на горизонтальную поверхность (дно сосу­да) равно произведению площади этой поверхности на величину давления на глубине по­гружения этой поверхности. На рисунке показан так называемый «гидравлический пара­докс», здесь величины силы давления на дно всех сосудов одинаковы, независимо от формы стенок сосудов и их физической высоты, т.к. площади доньев у всех сосудов оди­наковы, одинаковы и величины давлений.

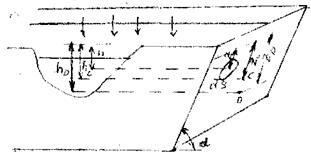
Сила давления на наклонную поверхность, погруженную в жидкость. Практическим примером такой поверхности может служить наклонная стенка сосуда. Для вывода урав-

нения и вычисления силы давления на стенку выберем следующую систему координат: ось ОХ направим вдоль пересечения плоскости свободной поверхности жидкости с на­клонной стенкой, а ось OZ направим вдоль этой стенки перпендикулярно оси ОХ. Тогда в качестве координатной плоскости XOZ будет выступать сама наклонная стенка. На плос­кости стенки выделим малую площадку 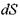, которую, в связи с малыми размерами можем считать горизонтальной. Величина давления на глубине площадки будет равна:

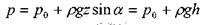
где: h - глубина погружения площадки относительно свободной поверхности жидкости (по вертика­ли).

Сила 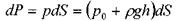давления 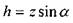dP на площадку:

Для определения силы давления

на всю смоченную часть наклонной стенки (часть площади стенки сосуда, расположенная ниже уровня свободной поверхности жидкости) необходимо проинтегрировать это урав­нение по всей смоченной части площади стенки S .

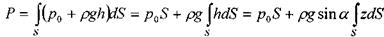
Интеграл 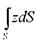представляет собой статический момент площади S относительно оси ОХ. Он, как известно, равен произведению этой площади на координату её центра тяжести z_c. Тогда окончательно:

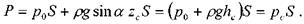
Таким образом, сила давления на наклонную плоскую поверхность, погружённую в жидкость равна смоченной площади этой поверхности на величину давления в центре тя­жести этой площади. Сила давления на плоскую стенку кроме величины и направления характеризуется также и точкой приложения этой силы, которая называется центром дав­ления.

Центр давления силы атмосферного давления p₀S будет находиться в центре тяже­сти площадки, поскольку атмосферное давление передаётся на все точки жидкости одина­ково. Центр давления самой жидкости на площадку можно определить исходя из теоремы о моменте равнодействующей силы. Согласно этой теореме момент равнодействующей

силы относительно оси ОХ будет равен сумме моментов составляющих сил относительно этой же оси.

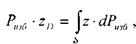
откуда: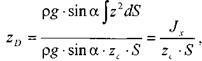

где: 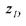- положение центра избыточного давления на вертикальной оси,

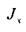- момент инерции площадки S относительно оси ОХ.

Отсюда центр давления (точка приложения равнодействующей силы избыточного давления) расположен всегда ниже центра тяжести площадки. В сучаях, когда внешнней действующей силой на свободную поверхность жидкости является сила атмосферного давления, то на стенку сосуда будут одновременно действовать две одинаковые по вели­чине и противоположные по направлению силы обусловленные атмосферным давлением (на внутреннюю и внешнюю стороны стенки). По этой причине реальной действующей несбалансированной силой остаётся сила избыточного давления.