Задачи для самостоятельной работы

1. Предположим, что 5 мужчин из 100 и 25 женщин из 10000 являются дальтониками. Наугад выбранное лицо страдает дальтонизмом. Какова вероятность того, что это мужчина? (считать, что мужчин и женщин одинаковое количество).

2. Прибор может работать в двух режимах: нормальном и ненормальном. Нормальный режим наблюдается в 80% всех случаев работы прибора, ненормальный – в 20%. Вероятность выхода прибора из строя за время t в нормальном режиме равно 0.1; в ненормальном – 0.7. Найти вероятность выхода прибора из строя за время t.

3. На трех дочерей – Юлю, Марину и Лену – в семье возложена обязанность мыть посуду. Поскольку Юля старшая, ей приходиться выполнять 40 % всей работы. Остальные 60 % работы приходятся поровну на Марину и Лену. Вероятность разбить что–нибудь из посуды (в течение одного мытья) для Юли, Марины и Лены равны соответственно: 0.02, 0.03, 0.05. Родители не знают, кто дежурил вечером, но они слышали звон разбитой посуды. Какова вероятность того, что посуду мыла: Юля; Марина; Лена?

4. В первой урне содержится 10 шаров, из них 8 белых, во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух наудачу взяли один шар. Найти вероятность того, что из двух шаров будет выбран белый.

5. Известно, что 96% выпускаемых заводом изделий отвечает стандарту. Упрощенная схема контроля признает пригодной стандартную продукцию с вероятностью 0.98 и нестандартную с вероятностью 0.05. Определить вероятность того, что изделие, прошедшее упрощенный контроль, отвечает стандарту.

6. В урне имеется N шаров, причем цвет каждого из них с равной вероятностью может быть белым или черным. Извлекаются последовательно K шаров, причем каждый раз после извлечения шар возвращается в урну. Какова вероятность того, что в урне содержатся только белые шары, если черные шары не извлекались?

7. Имеются три партии по 20 деталей каждая. В одной находятся две бракованных детали, в другой – четыре, в третьей – шесть. Извлеченные случайным образом из какой-то партии две детали оказались бракованными. Какова вероятность, что это была первая, вторая, третья партии?

8. Пусть некоторое насекомое с вероятностью 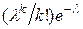, 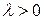кладёт 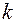яиц, а вероятность развития насекомого из яйца равна 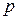. Найти вероятность того, что у насекомого будет: а) потомство; б) будет только один потомок.