Исходные положения метода гармонической линеаризации
Метод гармонической линеаризации (метод гармонического баланса) –. это приближенный (инженерный) метод, позволяющий исследовать собственные и вынужденные колебания, а также устойчивость нелинейных систем. Метод не имеет ограничений на порядок системы. Этот метод до настоящего времени строго не обаснован. Однако длительная практика применения доказала его эффективность.
Пусть имеем нелинейное звено рис. 2.1 с нелинейной статической характеристикой
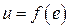 , (2.38)
, (2.38)
на вход которого подается гармонический сигнал 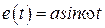 . Сигнал на выходе нелинейного звена будет не гармоническим, однако периодическим с тем же самым периодом
. Сигнал на выходе нелинейного звена будет не гармоническим, однако периодическим с тем же самым периодом 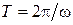 , т.е.
, т.е. 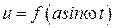 .
.
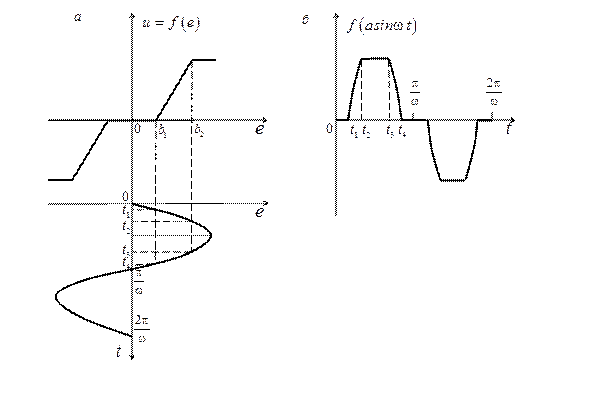
Рис. 2.15
На рис. 2.15 дана графическая иллюстрация преобразования гармонического сигнала нелинейной характеристикой, имеющей зону нечувствительности и насыщения.
Так как сигнал 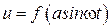 является периодическим с периодом
является периодическим с периодом 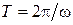 , то разложим его в ряд Фурье
, то разложим его в ряд Фурье
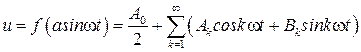 , (2.39)
, (2.39)
где
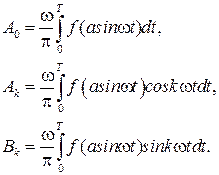 (2.40)
(2.40)
Коэффициенты ряда Фурье 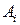 ,
, 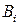 вычисляются по известной нелинейности
вычисляются по известной нелинейности 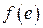 . Обычно амплитуды первой гармоники
. Обычно амплитуды первой гармоники 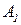 ,
, 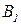 значительно больше амплитуд высших гармоник частот
значительно больше амплитуд высших гармоник частот 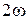 ,
, 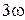 , ….
, ….
Сигнал с выхода нелинейного элемента в соответствии со структурой замкнутой системы рис. 2.2 поступает на вход линейной части систем с передаточной функцией 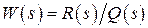 или с соответствующей АФЧХ
или с соответствующей АФЧХ 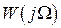 . Будем считать, что степень полинома
. Будем считать, что степень полинома 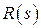 меньше степени полинома
меньше степени полинома 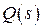 , что соответствует физически реализуемой системе. В этом случае
, что соответствует физически реализуемой системе. В этом случае 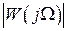 (АЧХ) с ростом
(АЧХ) с ростом 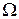 обязательно будет стремиться к нулю. Вид АЧХ приведен на рис. 2.16, где кривая 1 соответствует статической, а 2 − астатической системе. Здесь же приведены спектральные составляющие входного сигнала в соответствии с (2.39) основной частоты
обязательно будет стремиться к нулю. Вид АЧХ приведен на рис. 2.16, где кривая 1 соответствует статической, а 2 − астатической системе. Здесь же приведены спектральные составляющие входного сигнала в соответствии с (2.39) основной частоты 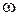 и высших гармоник
и высших гармоник 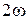 ,
, 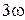 , ….
, ….
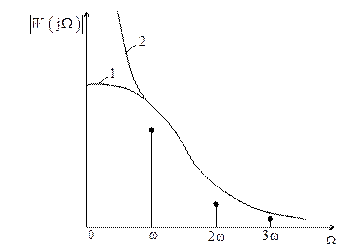
Рис. 2.16
В соответствии с рис. 2.16 линейная система отфильтрует высокочастотные составляющие и на выходе линейной части будет сигнал, близкий к гармоническому 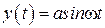 . Такое свойство линейной части будем называть свойством фильтра. Таким образом, если линейная часть системы является низкочастотным фильтром (выполняется гипотеза фильтра), то при определенных условиях в замкнутой системе при
. Такое свойство линейной части будем называть свойством фильтра. Таким образом, если линейная часть системы является низкочастотным фильтром (выполняется гипотеза фильтра), то при определенных условиях в замкнутой системе при 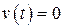 сигнал
сигнал 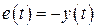 в установившемся режиме будет гармоническим или достаточно близким к гармоническому
в установившемся режиме будет гармоническим или достаточно близким к гармоническому
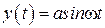 . (2.41)
. (2.41)
Выяснение выполнения таких условий и определения амплитуды 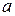 и частоты
и частоты 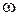 гармонического режима, возникающего в замкнутой системе, и составляет суть метода гармонического баланса. Колебания вида (2.41) будем называть симметричными. Они обычно возникают при отсутствии внешнего воздействия (
гармонического режима, возникающего в замкнутой системе, и составляет суть метода гармонического баланса. Колебания вида (2.41) будем называть симметричными. Они обычно возникают при отсутствии внешнего воздействия ( 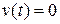 ), т.е. являются собственными, и при нечетной нелинейности
), т.е. являются собственными, и при нечетной нелинейности 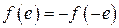 . При
. При 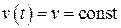 , либо при несимметричных нелинейностях относительно начала координат в разложении (2.39) появляется постоянная составляющая и появляются несимметричные колебания
, либо при несимметричных нелинейностях относительно начала координат в разложении (2.39) появляется постоянная составляющая и появляются несимметричные колебания
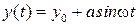 , (2.42)
, (2.42)
в которых определению подлежат три параметра 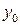 ,
, 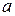 ,
, 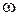 .
.
Рассмотрим связь входа и выхода нелинейного элемента в предположении, что на входе действует сигнал 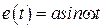 , а на выходе сигнал (2.39) без учета высших гармоник, т.е.
, а на выходе сигнал (2.39) без учета высших гармоник, т.е.
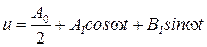 . (2.43)
. (2.43)
Первоначально будем рассматривать случай симметричных колебаний, т.е. считать 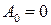 . Обозначим
. Обозначим 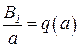 ,
, 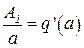 , тогда
, тогда
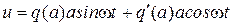 . (2.44)
. (2.44)
С учетом того, что 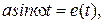
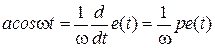 , где
, где 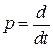 , получим
, получим
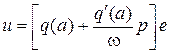 , (2.45)
, (2.45)
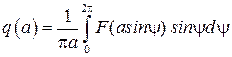 , (2.46)
, (2.46)
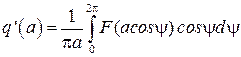 . (2.47)
. (2.47)
Выражение (2.45) является уравнением гармонической линеаризации нелинейности, а 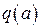 (2.46) и
(2.46) и 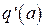 (2.47) называются коэффициентами гармонической линеаризации.
(2.47) называются коэффициентами гармонической линеаризации.
Из (2.45), приняв 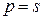 , находим гармонически линеаризованную передаточную функцию нелинейного элемента
, находим гармонически линеаризованную передаточную функцию нелинейного элемента
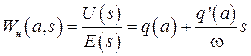 , (2.48)
, (2.48)
а при 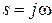 - амплитудно-фазовую характеристику нелинейного элемента
- амплитудно-фазовую характеристику нелинейного элемента
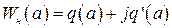 . (2.49)
. (2.49)
Особенностью (2.48), (2.49) является то, что передаточная функция зависит от амплитуды и частоты входного сигнала, а АЧХ не зависит от частоты, но зависит от амплитуды 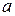 . Выражения (2.45), (2.48), (2.49) справедливы только для определенного типа входного сигнала − гармонического
. Выражения (2.45), (2.48), (2.49) справедливы только для определенного типа входного сигнала − гармонического 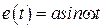 и при условии отсутствия высших гармоник на выходе нелинейного элемента. Последнее, предположительно, будет выполняться в замкнутой нелинейной САУ при выполнении гипотезы фильтра.
и при условии отсутствия высших гармоник на выходе нелинейного элемента. Последнее, предположительно, будет выполняться в замкнутой нелинейной САУ при выполнении гипотезы фильтра.
В случае несимметричных колебаний сигнал на выходе нелинейного элемента будет иметь вид
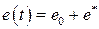 ,
, 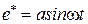 ,
,
а выражения (2.45), (2.46), (2.47) будут следующими:
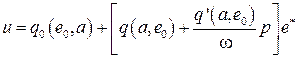 , (2.50)
, (2.50)
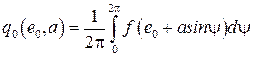 , (2.51)
, (2.51)
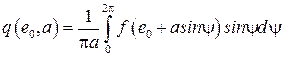 , (2.52)
, (2.52)
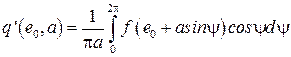 . (2.53)
. (2.53)
Дата добавления: 2022-02-05; просмотров: 529;











