Условия эквивалентности импульсных и непрерывных САУ
Рассмотрим разомкнутую импульсную систему, приведенную на рис. 1.5, б, передаточная функция ЭЛНЧ которой имеет вид 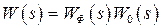 . Передаточная функция импульсной системы будет
. Передаточная функция импульсной системы будет 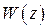 , а частотная характеристика
, а частотная характеристика 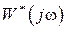 . Существует связь между частотными характеристиками ЭЛНЧ
. Существует связь между частотными характеристиками ЭЛНЧ 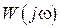 и частотной характеристикой импульсной системы
и частотной характеристикой импульсной системы 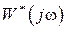 , которая имеет вид [4]:
, которая имеет вид [4]:
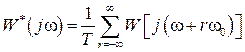 , (1.68)
, (1.68)
где, как и ранее, 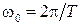 - частота дискретизации.
- частота дискретизации.
Итак, характеристика 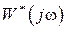 получается суммированием смещенных относительно друг друга вдоль оси
получается суммированием смещенных относительно друг друга вдоль оси 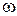 на частоту повторения
на частоту повторения 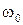 характеристик
характеристик 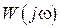 ЭЛНЧ, умноженных на
ЭЛНЧ, умноженных на 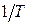 . Из (1.68) вещественные и мнимые части частотных характеристик
. Из (1.68) вещественные и мнимые части частотных характеристик
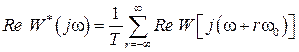 ,
,
(1.69)
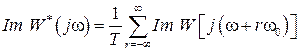 .
.
Предположим, что вещественная и мнимая частотные характеристики заданы на интервале частоты  от
от  до
до 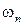 (
( 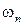 - полоса пропускания) и вне этого интервала равны нулю, а спектральные характеристики входного сигнала
- полоса пропускания) и вне этого интервала равны нулю, а спектральные характеристики входного сигнала 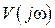 определены на некотором интервале
определены на некотором интервале 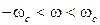 и равны нулю вне этого интервала. В этом случае, если
и равны нулю вне этого интервала. В этом случае, если 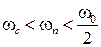 , справедливо следующее соотношение
, справедливо следующее соотношение
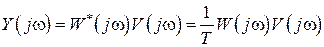 . (1.70)
. (1.70)
Итак, при выполнении условия 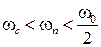 импульсная система с передаточной функцией
импульсная система с передаточной функцией 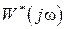 преобразует входной сигнал точно так же, как некоторая непрерывная система с передаточной функцией
преобразует входной сигнал точно так же, как некоторая непрерывная система с передаточной функцией 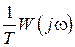 .
.
Фактически сформулирован аналог известной теоремы Котельникова: если спектр частот входного воздействия ограничен и лежит в диапазоне частот 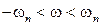 , то свойство системы с АИМ, у которой
, то свойство системы с АИМ, у которой 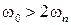 тождественны свойствам эквивалентной непрерывной системы с АФЧХ
тождественны свойствам эквивалентной непрерывной системы с АФЧХ 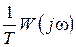 .
.
Частотные характеристики входного сигнала 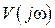 и системы
и системы 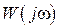 на практике реально не ограничены по частоте величинами
на практике реально не ограничены по частоте величинами 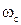 и
и 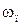 ,и можно говорить лишь об их малости при
,и можно говорить лишь об их малости при 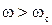 и
и 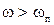 . Поэтому на практике условие сведения системы с АИМ к соответствующей непрерывной системе обычно ужесточают и требуют, чтобы
. Поэтому на практике условие сведения системы с АИМ к соответствующей непрерывной системе обычно ужесточают и требуют, чтобы
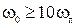 , (1.71)
, (1.71)
где 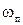 – частота, характеризующая полосу пропускания ЭЛНЧ.
– частота, характеризующая полосу пропускания ЭЛНЧ.
Для проверки выполнения (1.71) следует построить 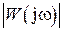 и найти
и найти 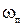 . Иногда вместо (1.71) легче воспользоваться другой более простой рекомендацией [6]:
. Иногда вместо (1.71) легче воспользоваться другой более простой рекомендацией [6]:
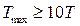 , (1.72)
, (1.72)
где 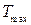 – максимальная постоянная времени передаточной функции
– максимальная постоянная времени передаточной функции 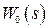 .
.
Использование 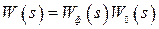 в качестве эквивалентной передаточной функции неудобно из-за присутствия в ней передаточной функции формирующего устройства, АФЧХ которого имеет вид
в качестве эквивалентной передаточной функции неудобно из-за присутствия в ней передаточной функции формирующего устройства, АФЧХ которого имеет вид
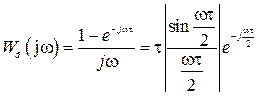 .
.
АЧХ и ФЧХ фиксирующего устройства будут:
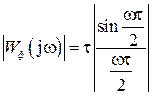 ,
, 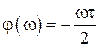 .
.
Соответственно АФЧХ эквивалентной непрерывной системы
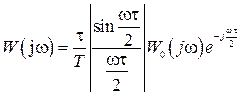 . (1.73)
. (1.73)
В основном методы анализа непрерывных линейных систем управления разработаны для случая, когда передаточная функция разомкнутой системы является дробно-рациональной относительно 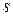 . Поэтому непосредственное исследование передаточной функции
. Поэтому непосредственное исследование передаточной функции
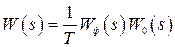 , (1.74)
, (1.74)
и частотных характеристик разомкнутой системы (1.73) затруднительно.
Рассмотрим возможные варианты дальнейшего упрощения моделей импульсных систем.
Если полагать в (1.73) 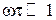 , то
, то 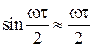 и
и 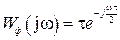 , а (1.74) превратится в следующее выражение:
, а (1.74) превратится в следующее выражение:
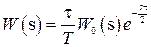 . (1.75)
. (1.75)
И, наконец, наиболее простой вид модель приобретает при условии, когда 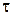 мало:
мало:
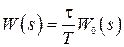 , (1.76)
, (1.76)
т.е. практически с точностью до множителя 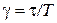 передаточные функции
передаточные функции 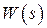 и
и 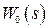 совпадают. Очевидно, при
совпадают. Очевидно, при 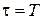 все сказанное соответствует случаю, когда формирующее устройство является фиксатором нулевого порядка.
все сказанное соответствует случаю, когда формирующее устройство является фиксатором нулевого порядка.
Для всех трех эквивалентных моделей (1.74), (1.75), (1.76) характерно то, что они тем более близки к исходной импульсной системе, чем ниже диапазон рассматриваемых частот, т.е. справедливы в низкочастотной области. Модель (1.74) более точная, но неудобная, модель (1.76) менее точная из всех трех типов.
Пример 1.11. Пусть 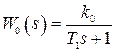 . В примерах 1.3 и 1.7 получена передаточная функция разомкнутой системы
. В примерах 1.3 и 1.7 получена передаточная функция разомкнутой системы 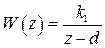 ,
, 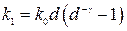 ,
, 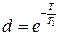 . Передаточная функция замкнутой системы
. Передаточная функция замкнутой системы 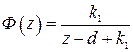 .
.
Далее будем рассматривать для наглядности случай 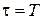 ,
, 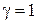 . В примерах 1.3 и 1.7 получены следующие результаты при анализе импульсной системы:
. В примерах 1.3 и 1.7 получены следующие результаты при анализе импульсной системы:
– область устойчивости
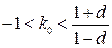 ;
;
– процессы будут носить монотонный характер 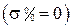 , если
, если
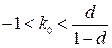 ;
;
– процессы будут носить колебательный характер 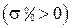 , если
, если
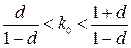 ;
;
– переходная функция 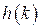 имеет вид
имеет вид
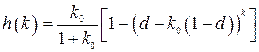 . (1.77)
. (1.77)
Основные выводы: в системе могут при определенных параметрах существовать как монотонные, так и колебательные процессы; коэффициент усиления 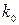 ограничен из условия устойчивости и не может быть сделан сколь угодно большим.
ограничен из условия устойчивости и не может быть сделан сколь угодно большим.
Вместо импульсной системы рассмотрим эквивалентную непрерывную систему с передаточной функцией вида (1.76). Так как в нашем примере 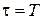 , то имеем
, то имеем 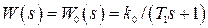 . Вид переходного процесса в замкнутой системе будет
. Вид переходного процесса в замкнутой системе будет
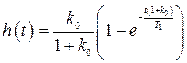 , (1.78)
, (1.78)
а условие устойчивости: 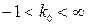 .
.
Итак, коэффициент 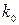 можно увеличивать до любого значения без потери устойчивости, а процессы (1.78) всегда будут монотонными.
можно увеличивать до любого значения без потери устойчивости, а процессы (1.78) всегда будут монотонными.
Для дискретных моментов времени 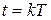 выражение (1.78) приобретает вид:
выражение (1.78) приобретает вид:
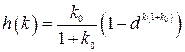 . (1.79)
. (1.79)
Очевидно, чем ближе величины 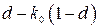 и
и 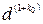 , тем процессы будут ближе между собой. Так как
, тем процессы будут ближе между собой. Так как 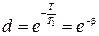 ,
, 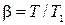 , то разлагая функции
, то разлагая функции 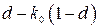 и
и 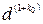 в ряд Тейлора относительно
в ряд Тейлора относительно 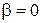 и ограничиваясь линейными членами, получим
и ограничиваясь линейными членами, получим
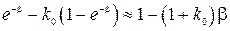 ,
,
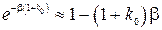 .
.
Итак, при малых 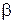 процессы в обеих системах идентичны и имеют монотонный характер.
процессы в обеих системах идентичны и имеют монотонный характер.
Однако, например, при 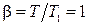 и
и 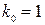 процесс в дискретной системе (1.77) будет
процесс в дискретной системе (1.77) будет 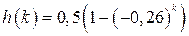 , а в соответствующей непрерывной системе (1.79)
, а в соответствующей непрерывной системе (1.79) 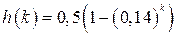 , т.е. эти процессы совершенно различны.
, т.е. эти процессы совершенно различны.
Рассмотрим второй случай замены импульсной системы непрерывной с передаточной функцией (1.75). Для нашего случая 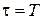 и
и
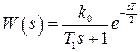 .
.
Передаточная функция замкнутой системы будет
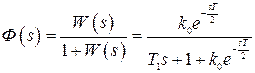 .
.
В этом случае приходим к системе автоматического управления с запаздыванием.
Уравнение, связывающее вход и выход системы, будет иметь вид
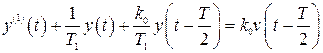
и является дифференциально-разностным. При 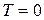 оно превращается в дифференциальное.
оно превращается в дифференциальное.
Условие устойчивости для такой системы
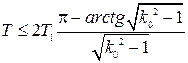 .
.
Здесь опять имеем ограничения на коэффициент усиления 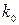 из условий устойчивости, как и в исходной импульсной системе.
из условий устойчивости, как и в исходной импульсной системе.
Наконец, замена импульсной системы непрерывной с передаточной функцией (1.74) приводит нас в данном случае к дифференциально-разностному уравнению второго порядка
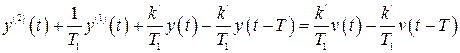 ,
, 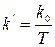 .
.
Дата добавления: 2022-02-05; просмотров: 241;











