Исследование цифровых систем автоматического управления

В первом приближении без учета нелинейностей характеристик АЦП и ЦАП и считая запаздывание малым 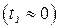, структура цифровой системы сводится к структуре системы с АИМ-1, к которой возможно применение всех изложенных выше методов анализа и синтеза импульсных систем.

Более подробно остановимся на функциях ЦВУ, которыми являются реализация дискретных алгоритмов управления и дискретной коррекции. Будем рассматривать линейные модели, реализуемые ЦВУ в общем случае. Этими моделями являются линейные разностные уравнения

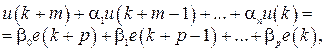(1.96)

где переменные 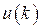, 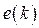представлены в виде цифровых кодов.

Применяя к (1.96) Z-преобразование, получим

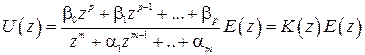, (1.97)

где 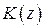– передаточная функция ЦВУ.

Линейное разностное уравнение (1.96) представляет собой алгоритм работы ЦВУ и может быть записано в виде

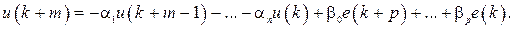(1.98)

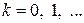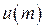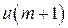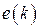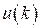Задавая , можно последовательно находить , , …, используя найденные на предыдущих этапах значения и . При таком подходе ЦВУ осуществляет три операции: умножение чисел, сложение чисел и запоминание чисел. Алгоритм возможен (реализуем) только при условии 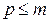. Если 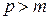, то для вычисления текущего значения 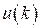следует знать ряд будущих значений входа, что физически невозможно. Итак, при 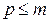передаточную функцию 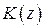будем называть физически реализуемой.

Рассмотрим несколько возможных алгоритмов управления и найдем для них передаточные функции.

1. Пропорциональный закон (по отклонению) .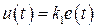

В дискретном случае 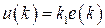, 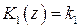. Это наиболее простой алгоритм. При этом ЦВУ выступает в роли элемента сравнения (сумматора), осуществляя операцию вычитания 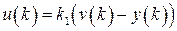в цифровой форме.

2. Дифференциальный закон (по производной от отклонения) 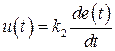. Найдем дискретный аналог этого закона

.

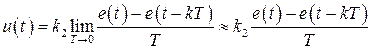Полагая 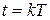, получим

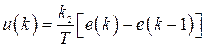. (1.99)

Применяя z-преобразование, найдем передаточную функцию

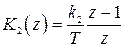. (1.100)

3. Интегральный закон (по интегралу от отклонения) 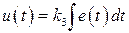. В зависимости от способа вычисления интеграла рассмотрим два варианта дискретных аналогов:

– по методу Эйлера

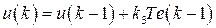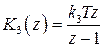, ; (1.101)

– по методу трапеций

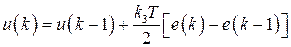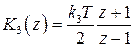, . (1.102)

Комбинируя рассмотренные законы 1, 2, 3, можно получить пропорционально-интегральный закон 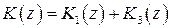, пропорционально-дифференциальный закон 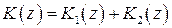и пропорционально-интегрально-дифференциальный .

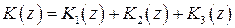Кроме реализации законов управления в дискретной форме ЦВУ используется также для реализации цифровой коррекции, т.е. синтеза передаточной функции 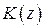, обеспечивающей цифровой системе заданные свойства.

Синтез цифровых САУ при их сведении к структуре рис. 1.11 может производиться тремя способами: при заданной 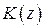введением непрерывной коррекции, т.е. изменением передаточной функции 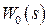; при заданной 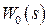отыскание дискретной коррекции 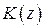; применением обоих подходов. О проблемах, связанных с этими путями коррекции, говорилось при рассмотрении линейных импульсных систем.

Пример 1.14. Пусть в цифровой САУ 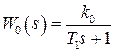. Требуется, чтобы в замкнутой системе ошибка по положению (статическая ошибка) была равна нулю, а скоростная при 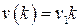была меньше заданной величины 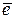. Передаточная функция 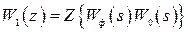для данного случая при 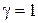получена в примерах 1.3 и 1.6 и имеет вид

, .

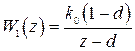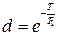Исходная система является статической и ошибка по положению не равна нулю. Для выполнения заданных требований реализуем на ЦВУ интегратор с передаточной функцией

,

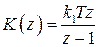тогда передаточная функция разомкнутой системы будет

.

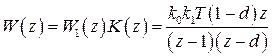Для такой системы в соответствии с результатом подраздела 1.8 статическая ошибка равна нулю, а скоростная будет

.

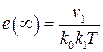Из условия 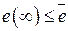, находим

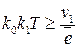. (1.103)

Если взять цифровой интеграл в виде 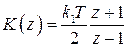, то получим тот же результат (1.103).

При выборе 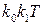следует также учесть условия устойчивости для данной системы. Характеристическое уравнение замкнутой системы будет 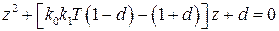. Применяя критерий (1.55), нетрудно получить условие устойчивости

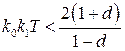, (1.104)

Таким образом, величина 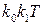выбирается исходя из заданной точности и обеспечения устойчивости из неравенства

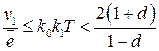. (1.105)

Соотношение (1.105) при известных 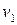, , 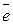, , 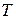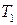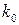позволяет выбрать 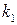. Пусть 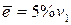, , 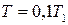, , 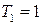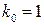тогда 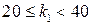. Так как проектируемая система должна обладать запасами устойчивости в пределах 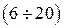дБ, что соответствует возможности увеличить коэффициент усиления в 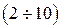раз без потерь устойчивости, то следует выбрать величину 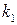для данного примера близкой к двадцати.