Решетчатые функции, разностные уравнения и дискретное преобразование Лапласа
Основой математической теории описания процессов в импульсных системах является аппарат решетчатых функций и разностных уравнений.
Решетчатой функцией 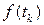 будем называть функцию, определенную для целочисленных значений аргумента
будем называть функцию, определенную для целочисленных значений аргумента 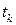 (
( 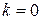 , 1, …). Впредь будем рассматривать
, 1, …). Впредь будем рассматривать 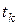 или
или 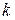 как дискретное время. Для ШИМ и АИМ
как дискретное время. Для ШИМ и АИМ 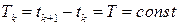 , поэтому функции будем обозначать
, поэтому функции будем обозначать 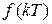 или
или 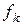 . Решетчатые функции
. Решетчатые функции 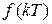 часто получаются из непрерывных
часто получаются из непрерывных 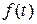 при замене
при замене 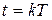 .
.
Аналогом производных непрерывных функций для решетчатых функций являются конечные разности. Конечная разность первого порядка (первая разность) для решетчатой функции 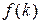 обозначается
обозначается 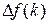 и определяется выражением
и определяется выражением
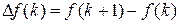 . (1.5)
. (1.5)
Вторая разность 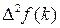 определяется как
определяется как
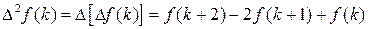 и т.д.
и т.д. 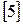 .
.
Аналогом операции интегрирования для решетчатой функции является операция суммирования
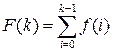 .
.
Очевидна связь 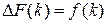 , а функция
, а функция 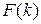 называется первообразной для решетчатой функции
называется первообразной для решетчатой функции 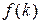 .
.
Аналогом дифференциальных уравнений непрерывных функций для решетчатых функций являются разностные уравнения, связывающие функцию 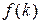 с ее разностями
с ее разностями 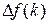 , …,
, …, 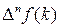 , или разностные уравнения, связывающие функцию
, или разностные уравнения, связывающие функцию 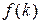 с ее значениями
с ее значениями 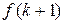 , …,
, …, 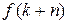 . В дальнейшем будем рассматривать второй вариант разностных уравнений.
. В дальнейшем будем рассматривать второй вариант разностных уравнений.
Линейные импульсные системы описываются линейными разностными уравнениями следующего вида:
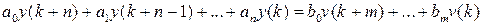 , (1.6)
, (1.6)
где 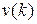 - заданная функция (вход),
- заданная функция (вход), 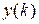 - искомая функция (решение разностного уравнения, выход),
- искомая функция (решение разностного уравнения, выход), 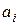 ,
, 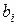 - постоянные коэффициенты, при этом чаще всего
- постоянные коэффициенты, при этом чаще всего 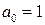 .
.
Величина 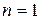 , 2, … определяет порядок разностного уравнения. Для полного задания при нахождении решения
, 2, … определяет порядок разностного уравнения. Для полного задания при нахождении решения 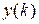 кроме вида функции
кроме вида функции 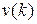 следует задать начальные условия искомого решения
следует задать начальные условия искомого решения 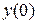 ,
, 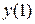 ,…,
,…, 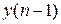 .
.
В случае непрерывных систем [1], описываемых линейными дифференциальными уравнениями, в теории автоматического управления широкое распространение находят методы исследования, базирующиеся на преобразованиях Лапласа и Фурье, где функция непрерывного аргумента 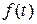 преобразуется в функцию комплексной переменной
преобразуется в функцию комплексной переменной 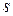 с помощью преобразования Лапласа
с помощью преобразования Лапласа
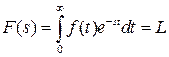 {
{ 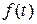 },
},
где 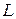 - символ прямого преобразования Лапласа,
- символ прямого преобразования Лапласа, 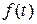 -оригинал,
-оригинал, 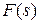 - изображение. Существует обратный переход от
- изображение. Существует обратный переход от 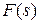 к
к 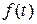 , т.е.
, т.е. 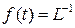 {
{ 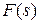 }, где
}, где 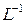 - символ обратного преобразования Лапласа.
- символ обратного преобразования Лапласа.
Аналогом преобразования Лапласа для решетчатых функций является дискретное преобразование Лапласа или 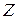 -преобразование, определяемое соотношениями
-преобразование, определяемое соотношениями
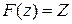 {
{ 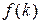 }=
}= 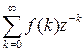 ,
,
(1.7)
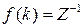 {
{ 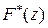 }=
}= 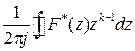 ,
,
где 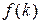 - решетчатая функция (оригинал),
- решетчатая функция (оригинал), 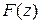 - изображение,
- изображение, 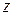 - комплексная переменная, а
- комплексная переменная, а 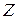 и
и 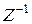 - соответственно символы прямого и обратного
- соответственно символы прямого и обратного 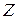 -преобразования.
-преобразования.
В литературе (например, [6]) приводятся таблицы соответствия между 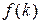 и
и 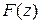 . Например, если
. Например, если 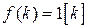 - единичная ступенчатая решетчатая функция, то
- единичная ступенчатая решетчатая функция, то 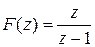 . Там же достаточно подробно рассматриваются свойства
. Там же достаточно подробно рассматриваются свойства 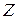 -преобразования. Например, если
-преобразования. Например, если 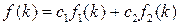 , где
, где 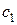 ,
, 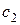 - постоянные, то
- постоянные, то 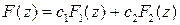 (свойство линейности).
(свойство линейности).
Другое свойство: пусть 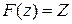 {
{ 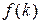 }, тогда
}, тогда 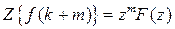 при условии, что
при условии, что 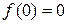 , …,
, …, 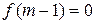 (теорема смещения).
(теорема смещения).
Если применить 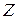 - преобразование к разностному уравнению (1.6), то с учетом вышеприведенных свойств нетрудно получить алгебраическиe уравнения относительно изображений:
- преобразование к разностному уравнению (1.6), то с учетом вышеприведенных свойств нетрудно получить алгебраическиe уравнения относительно изображений:
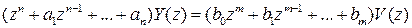 , (1.8)
, (1.8)
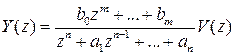 . (1.9)
. (1.9)
Функция комплексной переменной 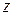
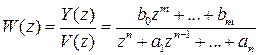 (1.10)
(1.10)
называется передаточной функцией и определяется как отношение изображений выхода 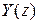 ко входу
ко входу 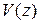 при нулевых начальных условиях переменных
при нулевых начальных условиях переменных 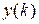 ,
, 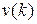 .
.
Наряду с решетчатыми функциями 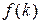 используются смещенные решетчатые функции, которые получаются из непрерывной функции
используются смещенные решетчатые функции, которые получаются из непрерывной функции 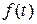 при замене
при замене 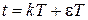 и обозначаются
и обозначаются 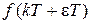 или в сокращенной записи
или в сокращенной записи 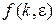 , где
, где 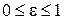 - параметр смещения. Уравнение (6) также можно записать относительно смещенных решетчатых функций, т.е. будем иметь разностное уравнение со смещенными аргументом.
- параметр смещения. Уравнение (6) также можно записать относительно смещенных решетчатых функций, т.е. будем иметь разностное уравнение со смещенными аргументом.
Для смещенных решетчатых функций 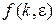 преобразование (1.7) будет иметь вид
преобразование (1.7) будет иметь вид
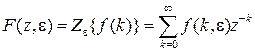 , (1.11)
, (1.11)
т.е. изображение будет зависеть от параметра 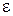 . При
. При 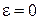 (1.7) и (1.11) совпадают.
(1.7) и (1.11) совпадают.
Итак, в рамках изложенного можно говорить о функциях: непрерывной 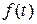 , решетчатой
, решетчатой 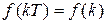 , смещенной решетчатой
, смещенной решетчатой 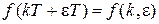 и соответственно об изображениях:
и соответственно об изображениях: 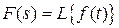 ,
, 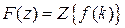 и
и 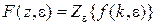 .
.
Существует однозначная связь между перечисленными функциями и изображениями [6]. Эти соотношения для наиболее употребительных функций приведены в табл.1.1. 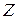 -преобразование получается из последнего столбца при
-преобразование получается из последнего столбца при 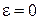 .
.
Таблица 1.1
| Непрерывная функция | Решетчатая функция | 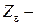 преобразование
для преобразование
для 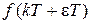
| |
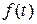
| 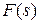
| ||
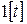
| 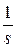
| 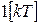
| 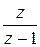
|
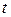
| 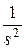
| 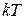
| 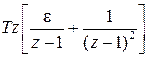
|
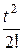
| 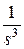
| 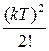
| 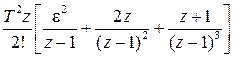
|
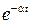
| 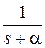
|
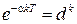
| 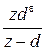 , , 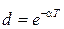
|
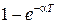
| 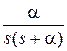
|
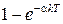
| 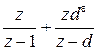
|
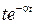
| 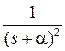
|
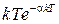
| 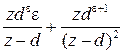
|
Отметим, что в литературе наряду с дискретным преобразованием Лапласа в форме 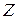 -преобразования используется так называемое
-преобразования используется так называемое 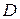 -преобразование, получаемое из (1.7), (1.11) заменой
-преобразование, получаемое из (1.7), (1.11) заменой 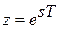 , т.е. изображения будут функциями комплексной переменной
, т.е. изображения будут функциями комплексной переменной 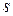 . Очевидно, свойства
. Очевидно, свойства 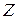 - и
- и 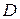 -преобразований во многом идентичны.
-преобразований во многом идентичны.
Решение разностного уравнения (1.8) при нулевых начальных условиях с использованием 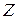 -преобразования имеет следующий алгоритм:
-преобразования имеет следующий алгоритм:
- по уравнению (1.8) находим передаточную функцию 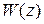 ;
;
- задавая вход 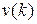 ,находим по таблицам изображение функции
,находим по таблицам изображение функции 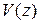 ;
;
- перемножая 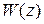 и
и 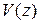 ,находим изображение
,находим изображение 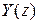 , которое обычно будет иметь вид
, которое обычно будет иметь вид 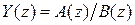 , где
, где 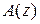 и
и 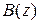 полиномы относительно
полиномы относительно 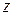 ;
;
- сложную дробно-рациональную функцию 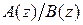 представляем в виде суммы простейших дробей первой степени
представляем в виде суммы простейших дробей первой степени
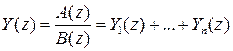 ;
;
- переходим от изображения 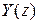 к оригиналу
к оригиналу 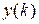
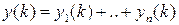 ,
,
где 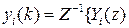
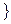 находим по таблицам.
находим по таблицам.
Пример 1.1. Найти решение разностного уравнения 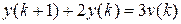 при нулевом начальном значении
при нулевом начальном значении 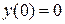 и воздействии вида единичной ступенчатой функции
и воздействии вида единичной ступенчатой функции 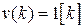 .
.
Находим 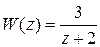 ,
, 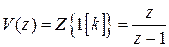 ,
, 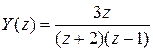 .
.
Представим 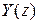 в виде следующей суммы
в виде следующей суммы 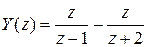 .
.
Из табл. 1.1 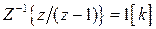 ,
, 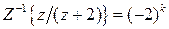 , тогда решение будет иметь вид
, тогда решение будет иметь вид
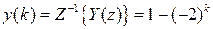 .
.
Дата добавления: 2022-02-05; просмотров: 175;










