Частотные характеристики импульсных систем

При описании и исследовании импульсных систем наряду с передаточными функциями и разностными уравнениями широкое распространение получили методы на базе частотных характеристик.

Если в формуле (1.7), определяющей прямое Z–преобразование, сделать замену переменной 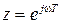, то получим соотношение

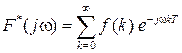, (1.23)

которое определяет прямое дискретное преобразование Фурье.

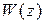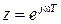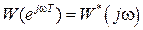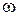Пусть известна передаточная функция разомкнутой системы , тогда после формальной замены получим , где – угловая частота.

Функция 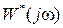называется амплитудно-фазовой частотной характеристикой (АФЧХ) импульсной системы. Далее знак 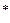будет относиться к частотным характеристикам импульсных систем. Характеристики без этого знака (например, 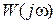) будут относиться к непрерывным системам.

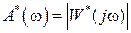называется амплитудной частотной характеристикой (АЧХ) системы, а 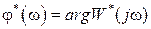– фазовой частотной характеристикой системы. Можно также ввести понятия вещественной и мнимой частотных характеристик.

Физический смысл частотных характеристик импульсной системы точно такой же, как и для непрерывной. Если на вход разомкнутой системы рис. 1.3 поступает гармонический сигнал 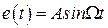, которому соответствует решетчатая функция 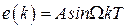, то на выходе в установившемся режиме будем иметь сигнал

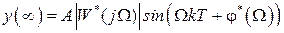, (1.24)

где 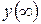здесь и далее будет обозначать установившееся значение сигнала или процесса при 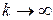или больших значений времени .

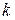Таким образом, АЧХ показывает, как изменяется амплитуда гармоники, а ФЧХ определяет величину фазового сдвига при прохождении гармоники через импульсную систему.

Так как 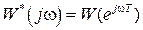, а 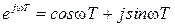, то в силу периодичности функци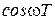й и 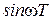частотные характеристики по отношению 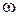являются периодическими функциями периода 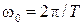, где здесь и далее 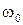– частота квантования (дискретизации) импульсного элемента.

Так же как для непрерывных систем и для импульсных САУ строятся график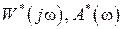и и 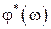на плоскости при изменении частоты 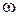. График 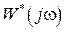является годографом на комплексной плоскости. Так как частотные характеристики периодические с периодом 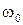, то их достаточно строить только на интервале частот от 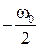до 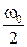. Более того 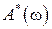– четная, а 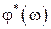нечетная функции своего аргумента, а годограф 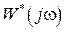симметричен относительно действительной оси. Поэтому характеристики обычно строятся на интервале частот от 0 до .

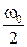Периодичность частотных характеристик отличает их от характеристик непрерывных систем, что является неудобным для получения логарифмических характеристик. Поэтому введем еще один класс частотных характеристик. В передаточной функции 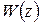сделаем замену комплексной переменной 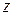на новую комплексную переменную 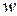по формулам:

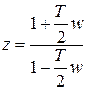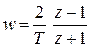, . (1.25)

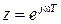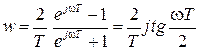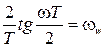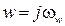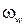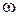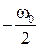Заменяя получим . Обозначим , тогда , где имеет размеренность угловой частоты и носит название псевдочастоты. При изменении от до 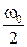псевдочастота изменяется от 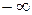до 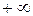. При малых 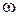частота 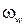близка к .

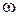Итак, заменяя 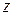на 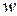, получим передаточную функцию 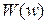, из которой, полагая 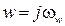получаем частотные характеристики 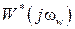, , 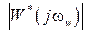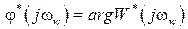– соответственно АФЧХ, АЧХ и ФЧХ относительно псевдочастоты.

Используя АЧХ и ФЧХ можно получить логарифмические характеристики 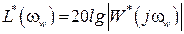– ЛАЧХ и 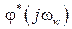– ЛФЧХ. Графики логарифмических характеристик строятся обычным образом, как и для непрерывных систем в логарифмическом масштабе.

В заключение рассмотрим одно из интересных свойств импульсных систем, связанное с периодичностью частотных характеристик. Пусть на вход разомкнутой системы поступает гармонический сигнал 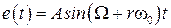, , 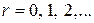которому соответствует решетчатая функция 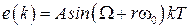. Тогда в соответствии с (1.24) в установившемся режиме на выходе будем иметь

.

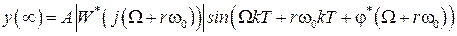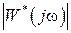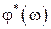В силу периодичности частотных характеристик и имеем 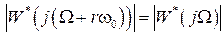, 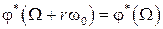. Кроме того с учетом 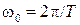можно записать 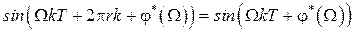. Окончательно получим 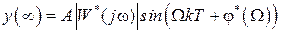, что совпадает с (1.24).

Итак, высокочастотная гармоника 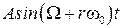и низкочастотная 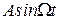на выходе разомкнутой импульсной системы дают один и тот же выходной сигнал. Это явление называется стробоскопическим эффектом, который заключается в переносе высокочастотных составляющих спектра входного сигнала в низкочастотную область.

Пример 1.3. Пусть 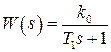, тогда передаточная функция разомкнутой системы в соответствии с (1.16) будет иметь вид

, , , .

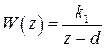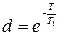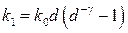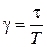Найдем основные частотные характеристики такой разомкнутой импульсной системы. Полагая 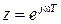с учетом 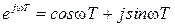будем иметь

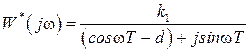, (1.26)

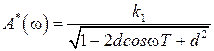, (1.27)

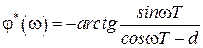. (1.28)

График АФЧХ (1.26) на комплексной плоскости представляет собой полуокружность при изменении частоты 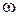от 0 до 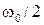(рис.1.6, а). При этом 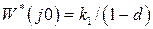, 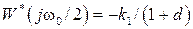. Радиус этой окружности равен 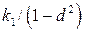, а центр лежит на оси в точке C с координатой .

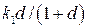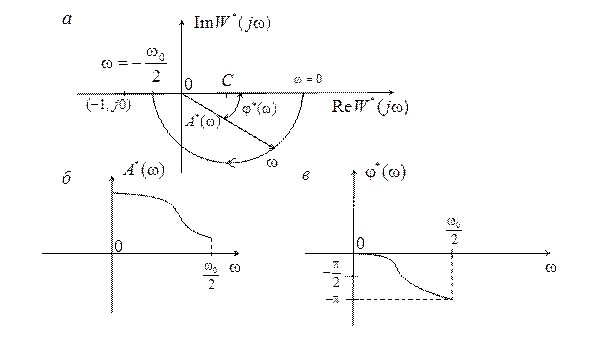
Рис. 1.6

Найдем логарифмические характеристики такой разомкнутой импульсной системы. В передаточной функции 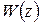сделаем замену 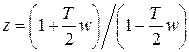, тогда после несложных преобразований получим

,

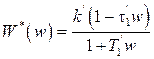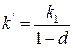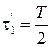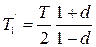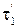где , , , а и 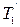можно рассматривать как постоянные времени. Заменяя 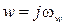, получим АФЧХ относительно псевдочастоты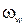

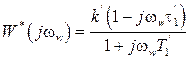, (1.29)

из которой находим АЧХ и ФЧХ

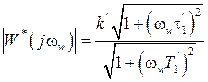, (1.30)

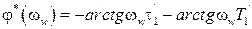. (1.31)

Логарифмическую амплитуду частотную характеристику получим из 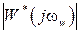, которая будет иметь вид

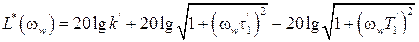. (1.32)

На рис. 1.7 приведены графики ЛАЧХ и ЛФЧХ построенные в соответствии с (1.32) и (1.31), в которых учтено, что всегда .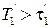

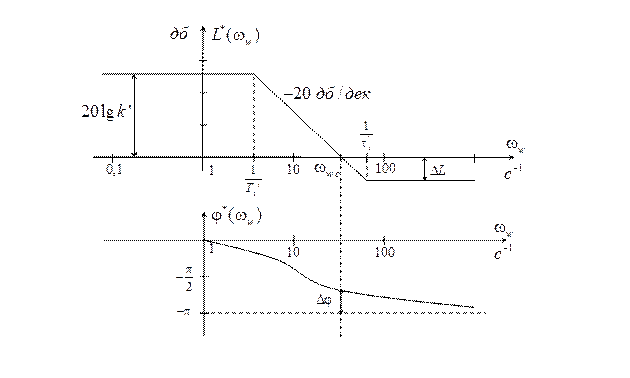
Рис. 1.7