Характеристики замкнутых импульсных систем
Рассмотрим базовую структуру импульсной САУ (рис. 1.3). Пусть найдена передаточная функция разомкнутой импульсной САУ 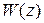 , связывающая
, связывающая 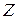 -изображения выхода
-изображения выхода 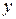 и сигнала ошибки
и сигнала ошибки 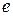 . Тогда
. Тогда 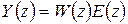 . Очевидно, что
. Очевидно, что 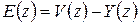 . Из этих уравнений нетрудно получить два соотношения:
. Из этих уравнений нетрудно получить два соотношения:
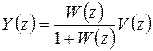 , (1.33)
, (1.33)
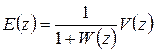 . (1.34)
. (1.34)
Введем следующие обозначения
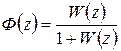 ,
, 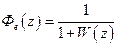 , (1.35)
, (1.35)
тогда (1.33), (1.34) запишутся как 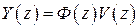 ,
, 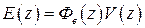 .
.
Функцию 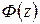 будем называть главной передаточной функций замкнутой импульсной системы, а
будем называть главной передаточной функций замкнутой импульсной системы, а 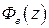 – передаточной функцией замкнутой импульсной системы по ошибке. Итак, зная
– передаточной функцией замкнутой импульсной системы по ошибке. Итак, зная 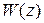 , нетрудно найти
, нетрудно найти 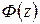 и
и 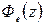 . Если
. Если 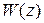 есть отношение двух полиномов некоторых степеней относительно
есть отношение двух полиномов некоторых степеней относительно 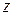 , то
, то 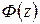 и
и 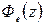 также будут отношением полиномов. Поэтому в конечном итоге
также будут отношением полиномов. Поэтому в конечном итоге 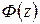 можно представить в виде
можно представить в виде
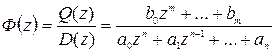 . (1.36)
. (1.36)
Используя (1.36) и связь 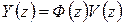 , нетрудно найти разностное уравнение замкнутой импульсной системы, связывающее вход и выход
, нетрудно найти разностное уравнение замкнутой импульсной системы, связывающее вход и выход
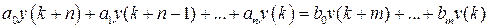 . (1.37)
. (1.37)
Кроме этого, введем еще одну важную характеристику системы – характеристическое уравнение замкнутой системы
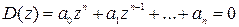 , (1.38)
, (1.38)
которое является алгебраическим уравнением n-ой степени. Полином 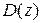 называется характеристическим полиномом замкнутой системы.
называется характеристическим полиномом замкнутой системы.
Введем также понятие частотных характеристик замкнутой системы. Делая в передаточной функции 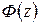 замену
замену 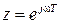 получим частотные характеристики, из которых наиболее часто используются
получим частотные характеристики, из которых наиболее часто используются 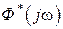 – АФЧХ замкнутой системы,
– АФЧХ замкнутой системы, 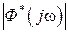 – АЧХ замкнутой системы и
– АЧХ замкнутой системы и 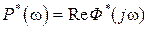 – вещественная частотная характеристика замкнутой системы. Физический смысл этих частотных характеристик такой же, как и для разомкнутых систем.
– вещественная частотная характеристика замкнутой системы. Физический смысл этих частотных характеристик такой же, как и для разомкнутых систем.
Следующим классом характеристик импульсной системы являются временные характеристики: весовая функция импульсной системы 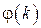 и переходная функция импульсной системы
и переходная функция импульсной системы 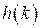 , определяемые следующими соотношениями:
, определяемые следующими соотношениями:
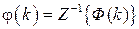 ,
, 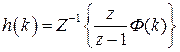 . (1.39)
. (1.39)
Физический смысл временных характеристик следующий. Если на вход замкнутой системы поступает сигнал в виде 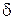 функции
функции 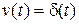 , изображение которой
, изображение которой 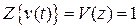 , то изображение выхода будет равно
, то изображение выхода будет равно 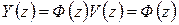 . Таким образом,
. Таким образом, 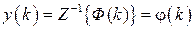 , т.е.
, т.е. 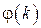 есть реакция системы на сигнал в виде
есть реакция системы на сигнал в виде 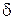 функции. Если же на вход системы поступает сигнал в виде единичного ступенчатого воздействия
функции. Если же на вход системы поступает сигнал в виде единичного ступенчатого воздействия 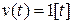 , изображение которого равно
, изображение которого равно 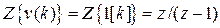 , то изображение выхода будет
, то изображение выхода будет 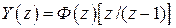 , а оригинал
, а оригинал 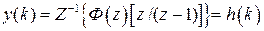 . Таким образом,
. Таким образом, 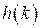 – это реакция системы на единичное ступенчатое воздействие. Функции
– это реакция системы на единичное ступенчатое воздействие. Функции 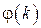 и
и 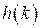 связаны следующим соотношением
связаны следующим соотношением 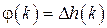 .
.
Если для системы известна весовая функция 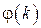 , то при заданном входе
, то при заданном входе 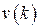 выход определяется следующим образом:
выход определяется следующим образом:
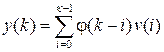 . (1.40)
. (1.40)
Выражение (1.40) представляет собой аналог интеграла свертки для импульсных систем.
Пример 1.4. Пусть 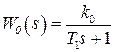 (см. пример 1.3), тогда
(см. пример 1.3), тогда 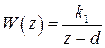 , где
, где 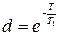 ,
, 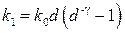 ,
, 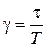 . Нетрудно найти основные характеристики замкнутой системы:
. Нетрудно найти основные характеристики замкнутой системы:
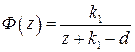 ,
, 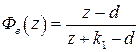 ,
,
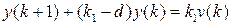 ,
,
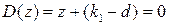 ,
,
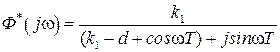 ,
,
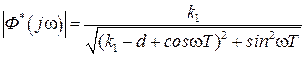 .
.
Дата добавления: 2022-02-05; просмотров: 200;











