Описание разомкнутых импульсных систем
Структура разомкнутой импульсной системы приведена на рис. 1.4.
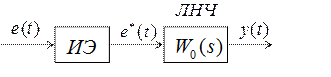
Рис. 1.4
Линейная непрерывная часть системы характеризуется передаточной функцией 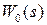 , а импульсный элемент законом модуляции
, а импульсный элемент законом модуляции 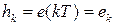 и постоянными значениями величин
и постоянными значениями величин 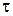 и
и 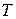 . Заметим, что сигналы
. Заметим, что сигналы 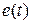 и
и 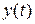 непрерывные, а
непрерывные, а 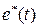 - последовательность прямоугольных импульсов, модулированных по амплитуде.
- последовательность прямоугольных импульсов, модулированных по амплитуде.
Рассмотрим получение разностного уравнения на простейшем примере. Пусть 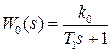 , тогда
, тогда 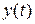 и
и 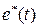 связаны дифференциальным уравнением
связаны дифференциальным уравнением 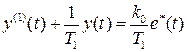 , которое легко решается.
, которое легко решается.
Обозначим значение координаты 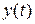 в произвольный момент времени квантования
в произвольный момент времени квантования 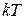 через
через 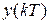 , тогда на интервале действия
, тогда на интервале действия 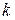 -ого импульса
-ого импульса 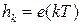 и закон изменения выхода будет
и закон изменения выхода будет
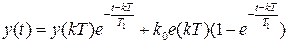 ,
, 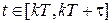 . (1.12)
. (1.12)
Найдем закон изменения 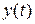 на интервале паузы в
на интервале паузы в 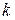 -ом периоде, когда
-ом периоде, когда 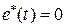 . Он будет иметь вид
. Он будет иметь вид
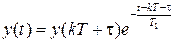 . (1.13)
. (1.13)
Полагая в (1.12) 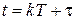 , найдем
, найдем 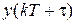 , подставим в (1.13) и после преобразований будем иметь
, подставим в (1.13) и после преобразований будем иметь
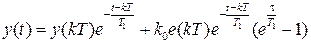 ,
, 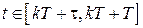 . (1.14)
. (1.14)
Положим в (1.14) 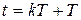 и, обозначая
и, обозначая 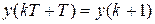 ,
, 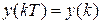 ,
, 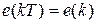 будем иметь
будем иметь
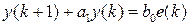 , (1.15)
, (1.15)
где 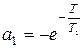 ,
, 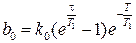 .
.
Итак, связь 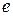 и
и 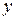 в дискретные моменты времени
в дискретные моменты времени 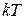 описывается линейным разностным уравнением первого порядка (частный случай (1.6)), коэффициенты которого
описывается линейным разностным уравнением первого порядка (частный случай (1.6)), коэффициенты которого 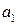 и
и 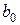 определены через параметры ИЭ и ЛНЧ.
определены через параметры ИЭ и ЛНЧ.
Аналогично, можно получить разностное уравнение при 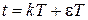 , т.е. для смещенных решетчатых функций
, т.е. для смещенных решетчатых функций 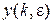 .
.
Применяя к (1.15) 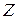 -преобразование, найдем для данного случая передаточную функцию
-преобразование, найдем для данного случая передаточную функцию
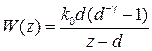
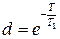 ,
, 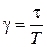 . (1.16)
. (1.16)
Для простейших случаев передаточных функций 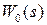 можно по этой методике получить дискретные передаточные функции разомкнутой системы. Ниже приведем таблицу для трех вариантов передаточной функции
можно по этой методике получить дискретные передаточные функции разомкнутой системы. Ниже приведем таблицу для трех вариантов передаточной функции 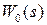 .
.
Таблица 1.2
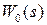
| 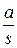
| 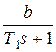
| 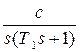
|
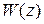
| 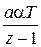
| 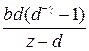
| 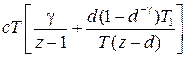
|
Если передаточная функция 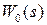 имеет более высокий порядок, но может быть представлена в виде суммы передаточных функций
имеет более высокий порядок, но может быть представлена в виде суммы передаточных функций 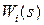 простейшего типа , то в этом случае находя по табл. 1.2
простейшего типа , то в этом случае находя по табл. 1.2 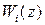 , можно получить общую передаточную функцию разомкнутой системы
, можно получить общую передаточную функцию разомкнутой системы
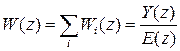 .
.
Рассмотрим другой способ получения передаточной функции разомкнутой системы, излагаемый практически в любом учебнике. Структура на рис. 1.4 может быть представлена в виде, изображенном на рис. 1.5, а.
 |
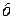

Рис.1.5
На рис. 1.5, а импульсный элемент представлен в виде идеального элемента (ИИЭ) или ключа и формирующего устройства (ФУ). Ключ периодически замыкается с периодом 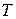 и формирует последовательность импульсов в виде
и формирует последовательность импульсов в виде 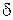 -функций, площадь которых равна
-функций, площадь которых равна 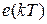 . ФУ формирует последовательность прямоугольных импульсов
. ФУ формирует последовательность прямоугольных импульсов 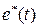 , амплитуда которых равна
, амплитуда которых равна 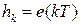 .
.
По определению 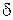 - функция описывается так:
- функция описывается так:
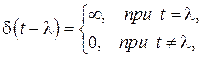
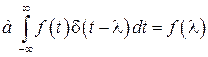 .
.
Разумеется, физически ИИЭ не существует, однако такое математическое представление ИЭ отражает физику процессов в исходной структуре рис.1.3. Объединяя передаточные функции 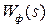 и
и 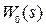 , приходим к структуре рис.1.5, б, где ЭЛНЧ – эквивалентная линейная непрерывная часть с передаточной функцией
, приходим к структуре рис.1.5, б, где ЭЛНЧ – эквивалентная линейная непрерывная часть с передаточной функцией 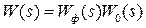 . В случае прямоугольных импульсов
. В случае прямоугольных импульсов 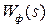 имеет вид
имеет вид
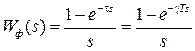 , (1.17)
, (1.17)
где 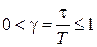 .
.
Если 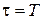 ,
, 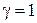 , то такое формирующее устройство называют фиксатором или экстраполятором нулевого порядка.
, то такое формирующее устройство называют фиксатором или экстраполятором нулевого порядка.
Если рассматривать 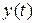 для
для 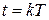 , т.е.
, т.е. 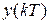 и ввести изображения решетчатых функций
и ввести изображения решетчатых функций 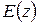 ,
, 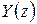 , то связь входа и выхода в области изображений будет
, то связь входа и выхода в области изображений будет 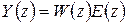 , где передаточную функцию дискретной разомкнутой системы можно определить по выражению [6]
, где передаточную функцию дискретной разомкнутой системы можно определить по выражению [6]
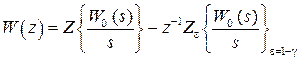 . (1.18)
. (1.18)
Отметим, что Z–преобразование применяется к решетчатым функциям. Однако каждой решетчатой функции 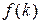 соответствует непрерывная
соответствует непрерывная 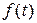 , а ей некоторое изображение
, а ей некоторое изображение 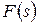 . Поэтому
. Поэтому 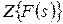 будем понимать как символичную запись
будем понимать как символичную запись 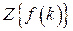 .
.
Алгоритм применения формулы (1.18) следующий. Если 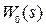 имеет высокий порядок, то
имеет высокий порядок, то 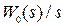 представляют в виде суммы простейших (табличных) слагаемых. Далее по таблицам
представляют в виде суммы простейших (табличных) слагаемых. Далее по таблицам 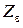 –преобразования находят изображения каждого слагаемого и суммируют их. В результате получают изображение
–преобразования находят изображения каждого слагаемого и суммируют их. В результате получают изображение 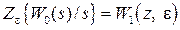 . Полагая в
. Полагая в 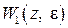
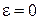 , получают первое слагаемое в (1.18) и, полагая
, получают первое слагаемое в (1.18) и, полагая 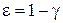 , – второе.
, – второе.
Наиболее часто используется случай фиксатора нулевого порядка ( 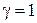 ). В этом случае формула (1.18) упрощается и имеет вид
). В этом случае формула (1.18) упрощается и имеет вид
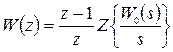 . (1.19)
. (1.19)
В наиболее общем случае передаточная функция 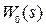 может быть записана в виде
может быть записана в виде 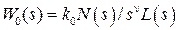 . При этом всегда степень полинома
. При этом всегда степень полинома 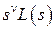 больше степени полинома
больше степени полинома 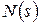 , а
, а 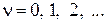 характеризует порядок астатизма. В этом случае передаточная функция импульсной системы будет иметь вид
характеризует порядок астатизма. В этом случае передаточная функция импульсной системы будет иметь вид
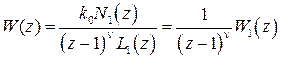 , (1.20)
, (1.20)
причем степени полиномов 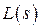 и
и 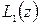 будут равны.
будут равны.
Для импульсной системы понятие порядка астатизма сохраняется, т.е. передаточная функция (1.20) соответствует импульсной системе с астатизмом 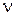 -го порядка.
-го порядка.
Пример 1.2. Найти передаточную функцию разомкнутой импульсной системы, если 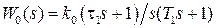 . Представим
. Представим 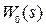 в виде суммы двух слагаемых
в виде суммы двух слагаемых
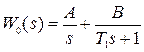 ,
,
где 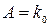 ,
, 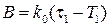 .
.
Воспользуемся табл. 1.2, тогда
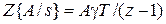 ,
, 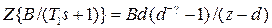 .
.
Таким образом,
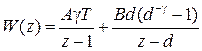 . (1.21)
. (1.21)
Теперь воспользуемся формулой (1.18) и найдем
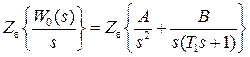 .
.
По таблицам Z–преобразования [6] (либо таблица 1.1) находим
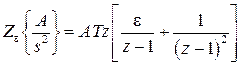 ,
,
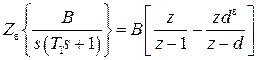 .
.
Таким образом, имеем
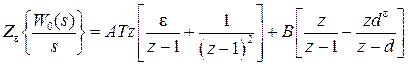 ,
,
откуда находим 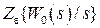 при
при 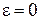 и
и 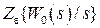 при
при 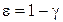 и подставляем их в (1.18). После преобразований приходим к выражению (1.19). Как и следовало ожидать, оба способа дали одинаковую передаточную функцию, которую можно записать и так
и подставляем их в (1.18). После преобразований приходим к выражению (1.19). Как и следовало ожидать, оба способа дали одинаковую передаточную функцию, которую можно записать и так
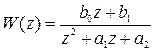 , (1.22)
, (1.22)
где 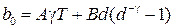 ,
, 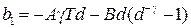 ,
, 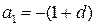 ,
, 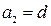 , а коэффициенты
, а коэффициенты 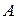 и
и 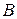 определены выше.
определены выше.
Если в приведенных выражениях положить 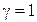 , то получим передаточную функцию для случая, когда ФУ является фиксатором нулевого порядка.
, то получим передаточную функцию для случая, когда ФУ является фиксатором нулевого порядка.
Дата добавления: 2022-02-05; просмотров: 212;











