Процессы в импульсных системах
Под процессом в импульсной САУ будем понимать изменение во времени некоторых координат, характеризующих систему. Чаще всего исследуется поведение системы по отношению к выходной координате 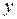 или по отношению к сигналу ошибки. Будем рассматривать все процессы для дискретных моментов времени
или по отношению к сигналу ошибки. Будем рассматривать все процессы для дискретных моментов времени 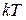 , т.е. в виде решетчатых функций
, т.е. в виде решетчатых функций 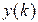 ,
, 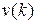 и т.д. Процессы в САУ возникают за счет приложения внешних воздействий (управляющих, возмущений и т.п.), либо за счет изменения значений внутренних координат системы (вариации начальных условий).
и т.д. Процессы в САУ возникают за счет приложения внешних воздействий (управляющих, возмущений и т.п.), либо за счет изменения значений внутренних координат системы (вариации начальных условий).
Исходными характеристиками при анализе процессов являются разностное уравнение замкнутой системы, главная передаточная функция системы 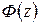 , либо АФЧХ замкнутой системы
, либо АФЧХ замкнутой системы 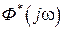 .
.
Методы вычисления процессов можно разделить на три категории: аналитические, графоаналитические и методы моделирования с использованием ЭВМ.
С математической точки зрения вычисление процессов – это нахождение решения разностного уравнения (1.37). В теории разностных уравнений доказано, что общее решение уравнения (1.37) всегда представимо в виде суммы двух слагаемых
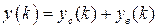 , (1.41)
, (1.41)
где 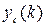 – свободная составляющая общего решения, а
– свободная составляющая общего решения, а 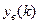 – вынужденная составляющая. Свободная составляющая обусловлена ненулевыми начальными условиями по переменной
– вынужденная составляющая. Свободная составляющая обусловлена ненулевыми начальными условиями по переменной 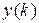 и, если они равны нулю, то
и, если они равны нулю, то 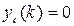 . Вынужденная обусловлена входным воздействием
. Вынужденная обусловлена входным воздействием 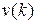 и, если
и, если 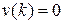 , то
, то 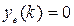 .
.
Для оценки динамических свойств системы обычно ищется 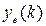 и наиболее часто для двух видов входного сигнала
и наиболее часто для двух видов входного сигнала 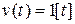 – единичной ступенчатой функции и
– единичной ступенчатой функции и 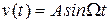 – гармонического воздействия, которым соответствуют решетчатые функции
– гармонического воздействия, которым соответствуют решетчатые функции 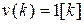 ,
, 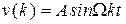 . Реакция системы на сигнал
. Реакция системы на сигнал 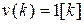 , как отмечено выше, это переходная функция замкнутой системы
, как отмечено выше, это переходная функция замкнутой системы 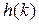 .
.
Типичный вид функции 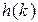 приведен на рис. 1.8, на котором представлен
приведен на рис. 1.8, на котором представлен
график решетчатой функции 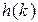 и непрерывная функция – огибающая.
и непрерывная функция – огибающая.

Рис. 1.8
Величина 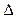 – задается, а
– задается, а 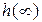 – установившиеся значение функции
– установившиеся значение функции 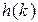 . Используя график, введем два важнейших показателя качества системы, характеризующие ее динамические свойства: перерегулирование
. Используя график, введем два важнейших показателя качества системы, характеризующие ее динамические свойства: перерегулирование
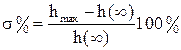 ,
,
которое измеряется в процентах, и время регулирования 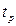 , определяемое как момент времени, когда переходная функция
, определяемое как момент времени, когда переходная функция 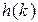 , “войдет” в область
, “войдет” в область 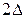 и будет оставаться там при
и будет оставаться там при 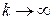 . На рис. 1.8
. На рис. 1.8 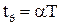 , где
, где 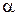 – целое число. Обычно
– целое число. Обычно 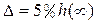 . Область
. Область 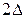 будем называть
будем называть 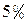 трубкой.
трубкой.
Рассмотрим аналитический способ вычисления переходной функции замкнутой системы 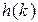 . Пусть задана передаточная функция замкнутой системы в виде
. Пусть задана передаточная функция замкнутой системы в виде 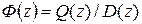 , где
, где 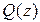 и
и 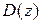 полиномы степеней
полиномы степеней 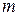 и
и 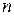 , причем
, причем 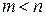 . Тогда при входном сигнале
. Тогда при входном сигнале 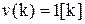 , изображение которого равно
, изображение которого равно 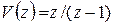 , изображение выходного сигнала будет
, изображение выходного сигнала будет
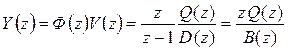 .
.
Рассмотрим идею получения 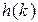 для простейшего случая. Пусть характеристическое уравнение
для простейшего случая. Пусть характеристическое уравнение 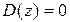 имеет простые корни
имеет простые корни 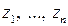 (полюса передаточной функции
(полюса передаточной функции 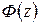 ), тогда дробно-рациональная функция
), тогда дробно-рациональная функция 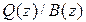 разлагается на сумму простейших первого порядка
разлагается на сумму простейших первого порядка
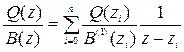 ,
, 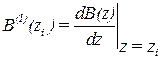 ,
,
где считаем 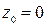 . С учетом того, что
. С учетом того, что 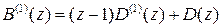 будем иметь
будем иметь
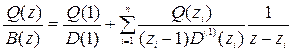 .
.
Таким образом, изображение 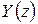 будет иметь вид
будет иметь вид
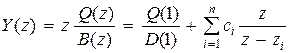 ,
,
где 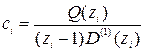 .
.
Каждое слагаемое под знаком суммы является табличным, т.е. для него легко найти оригинал. Окончательно, переходя к оригиналам 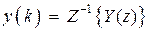 и обозначая
и обозначая 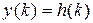 будем иметь
будем иметь
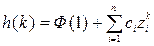 (1.42)
(1.42)
Первое слагаемое в (1.42) характеризует установившуюся (постоянную) составляющую, а второе – переходную.
В случае кратных корней характеристического уравнения 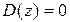 в литературе [6] приводят соответствующие выражения для вычисления
в литературе [6] приводят соответствующие выражения для вычисления 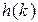 .
.
Недостатком такого подхода является необходимость вычисления корней алгебраических уравнений. Кроме того, после получения аналитического выражения, требуется строить график 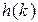 для оценки вида переходного процесса и параметров
для оценки вида переходного процесса и параметров 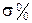 и
и 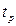 . Обычно такой подход применим для систем не выше третьего порядка.
. Обычно такой подход применим для систем не выше третьего порядка.
Существуют графо-аналитические способы построения переходного процесса 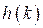 , базирующиеся на вещественной частотной характеристике замкнутой системы
, базирующиеся на вещественной частотной характеристике замкнутой системы 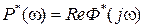 . Эти методы изложены, например, в [4], однако в настоящее время мало применяются.
. Эти методы изложены, например, в [4], однако в настоящее время мало применяются.
Наиболее распространенный в настоящее время путь вычисления и построения переходной функции 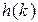 – это компьютерное моделирование.
– это компьютерное моделирование.
Второй тип процессов, исследуемых в импульсных системах, это процессы, вызванные гармоническими входными сигналами вида 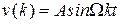 . Наиболее просто они определяются для случая установившегося режима (для больших значений дискретного времени
. Наиболее просто они определяются для случая установившегося режима (для больших значений дискретного времени 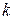 ). В этом случае исходной характеристикой является АФЧХ системы
). В этом случае исходной характеристикой является АФЧХ системы 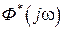 . После вычисления АЧХ как
. После вычисления АЧХ как 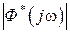 и ФЧХ как
и ФЧХ как 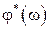 определяется выходной гармонический сигнал в установившемся режиме
определяется выходной гармонический сигнал в установившемся режиме
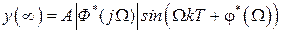 . (1.43)
. (1.43)
Итак, вычисляя 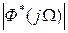 и
и 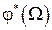 , найдем амплитуду гармонического сигнала на выходе
, найдем амплитуду гармонического сигнала на выходе 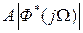 и сдвиг его по фазе
и сдвиг его по фазе 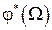 относительно входа.
относительно входа.
Одним из способов вычисления процессов в импульсной системе при любом законе изменения входной величины является рекуррентный пошаговый способ решения разностного уравнения (1.37). Рассмотрим разностное уравнение примера 1.1: 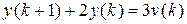 при
при 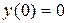 и
и 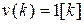 ,
, 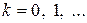 . Уравнение запишем в виде
. Уравнение запишем в виде
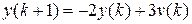 .
.
Будем последовательно задавать значения 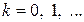 и т. д., тогда при
и т. д., тогда при 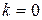 имеем
имеем 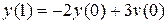 , но т.к. задано
, но т.к. задано 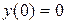 ,
, 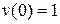 , то
, то 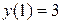 .
.
При 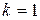 имеем
имеем 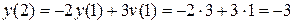 . При
. При 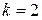 получим
получим 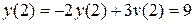 и т. д. Это совпадает с результатом аналитического решения
и т. д. Это совпадает с результатом аналитического решения 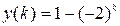 , полученного ранее в примере 1.1.
, полученного ранее в примере 1.1.
Рассмотрим общий случай уравнения (1.37), для чего представим его в следующем виде (принимаем 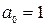 ):
):
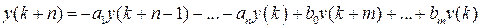 .
.
Полагаем следующие начальные условия 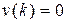 при
при 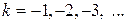 ,
, 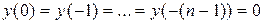 , вход
, вход 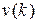 задан для
задан для 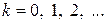 . Последовательно для
. Последовательно для 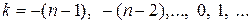 найдем
найдем 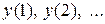 .
.
В импульсных системах, в отличие от непрерывных, при определенных параметрах системы возможно существование процессов “конечной длительности”, т.е. достигающих установившегося положения за конечный промежуток времени.
Если в импульсной системе путем подбора параметров ИЭ и ЛНЧ можно в передаточной функции замкнутой системы (1.36) сделать все 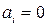 ,
, 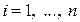 ,
, 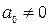 (далее полагаем
(далее полагаем 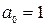 ), то передаточная функция (1.36) будет иметь вид
), то передаточная функция (1.36) будет иметь вид
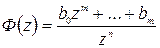 ,
,
а разностное уравнение (1.37) соответственно будет
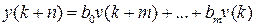 .
.
Задавая 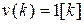 ,
, 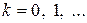 ,
, 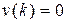 при
при 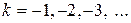 , а также
, а также 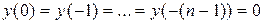 , можно вычислить переходную функцию
, можно вычислить переходную функцию 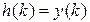 . При этом, начиная с n-го момента времени ее значения будут постоянными
. При этом, начиная с n-го момента времени ее значения будут постоянными 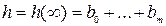 , т.е. переходной процесс заканчивается за
, т.е. переходной процесс заканчивается за 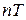 интервалов. Пусть, например, имеем
интервалов. Пусть, например, имеем 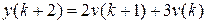 ,
, 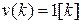 ,
, 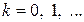 ,
, 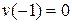 ,
, 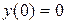 ,
, 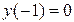 , тогда найдем
, тогда найдем 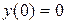 ,
, 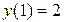 ,
, 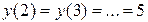 .
.
Итак, в системах с конечной длительностью процессов всегда время регулирования 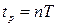 .
.
Пример 1.5. Пусть передаточная функция 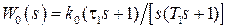 , тогда (см. пример 1.2) передаточная функция разомкнутой системы будет
, тогда (см. пример 1.2) передаточная функция разомкнутой системы будет
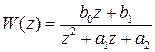 ,
,
где 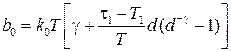 ,
, 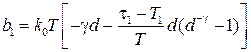 ,
, 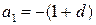 ,
, 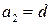 ,
, 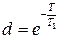 .
.
Пусть 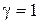 ,
, 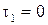 ,
, 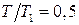 ,
, 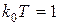 . Тогда с учетом
. Тогда с учетом 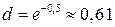 , нетрудно вычислить коэффициенты
, нетрудно вычислить коэффициенты 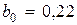 ,
, 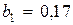 ,
, 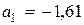 ,
, 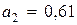 .
.
Передаточная функция разомкнутой системы в этом случае будет
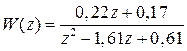 ,
,
а замкнутой системы
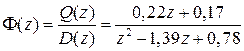 .
.
Округляя числа, получим окончательное выражение для расчетов
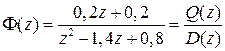 .
.
Корни характеристического уравнения 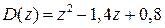 будут
будут 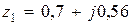 ,
, 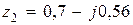 . Находим величины, входящие в (1.42). Так как
. Находим величины, входящие в (1.42). Так как 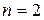 , получим
, получим 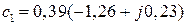 ,
, 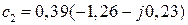 ,
, 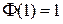 . Таким образом, будем иметь
. Таким образом, будем иметь
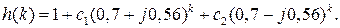
После преобразования комплексных чисел с использованием известных правил получаем окончательно
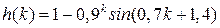 .
.
Пример 1.6. Пусть 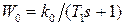 , тогда (см. пример 1.4)
, тогда (см. пример 1.4) 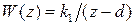 ,
, 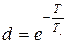 ,
, 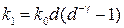 . Передаточная функция замкнутой системы имеет вид
. Передаточная функция замкнутой системы имеет вид 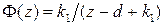 . Найдем
. Найдем 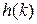 при
при 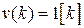 . Очевидно,
. Очевидно, 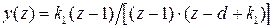 . По таблице 1 для данного изображения находим оригинал
. По таблице 1 для данного изображения находим оригинал
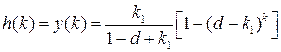 .
.
Установившийся процесс в такой системе, при 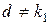 и
и 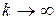 , будет
, будет 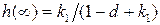 . Если
. Если 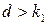 , процесс будет монотонным, а если
, процесс будет монотонным, а если 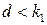 - колебательным. Пусть выполняется условие
- колебательным. Пусть выполняется условие 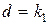 , т.е.
, т.е. 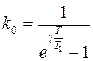 ,
, 
 что всегда выполнимо. В этом случае имеем систему с процессами конечной длительности, т.е.
что всегда выполнимо. В этом случае имеем систему с процессами конечной длительности, т.е. 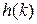 будет
будет 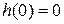 ,
, 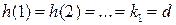 . Процесс в системе заканчивается через один период
. Процесс в системе заканчивается через один период 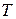 .
.
Дата добавления: 2022-02-05; просмотров: 288;











