Параллельные алгоритмы решения задач линейной алгебры

Пример №2.2. Пусть требуется вычислить скалярное произведение векторов а и b:
X₂₂ = а ^т b = S а_i b_i (i = 1…n; n = 4), (2.5)
где т – символ транспонирования вектора.

ПФ последовательного алгоритма решения этой задачи на однопроцессорном компьютере (p = 1) можно представить в виде табл. 2.2, где ярусы расположены горизонтально:

Табл. 2.2. Вычисление величины X22 на однопроцессорном компьютере (Пример №2.2)

Высота ПФ (табл.2.2)H₁= 7, ширина B₁= 1.

ПФ алгоритма решения этой же задачи на 4-процессорной ПВМ (p = 4) можно представить в виде табл. 2.3:

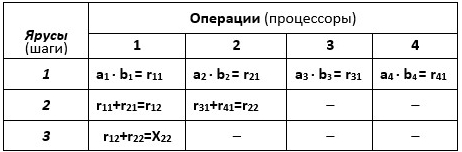
Табл. 2.3. Вычисление величины X22 на 4-процессорной ПВМ (Пример №2.2)

Высота ПФ (табл.2.3)H₄= 3, ширина – B₄= 4.

В соответствии с п.2.2. определим основные характеристики алгоритма, ПФ которого представлена в табл.2.3.
а) Ускорение S₄ = H₁ / H₄ = 7 / 3 =2.33.
б) ЭффективностьE₄ = S₄ / 4 = 2.33 / 4 = 0.58.
в) Высота H₄ = 3.
г) Загруженность процессоров : Z₄ = (7 / 12) 100% = 58.3%.

д) Устойчивость алгоритма. Сравнивая схемы вычислений табл.2.2 и табл.2.3, можно видеть, что они реализуют разные алгоритмы. При точных вычислениях они дадут одинаковые результаты, но в условиях влияния ошибок округлений результаты будут разными. Другими словами, эти алгоритмы обладают разной степенью устойчивости к ошибкам округления. Следует отметить, что устойчивость параллельных алгоритмов при большом числепроцессоров хуже устойчивости последовательных алгоритмов, реализуемых на однопроцессорных компьютерах.

Теперь построим ПФ алгоритма решения той же задачи на 2-процессорной ПВМ (табл.2.4).

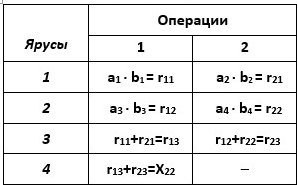
Табл. 2.4. Вычисление величины X22 на 2-процессорной ПВМ (Пример №2.2)

Определим характеристики алгоритма, ПФ которого представлена в табл.2.4:
а) ускорение S₂ = H₁ / H₂ = 7 / 4 = 1,75;
б) эффективностьE₂ = 1,75 / 2 = 0,875;
в) высота H₂ = 4;
г) загруженность процессоров : Z₂ = (7 / 8) 100% = 87,5%;
д) устойчивость алгоритмов табл.2.3 и табл.2.4 будут примерно одинаковыми, поскольку число промежуточных результатов (округлений) одно и то же.

Сравнивая алгоритмы вычислений табл.2.3 и табл.2.4, можно отметить, что для решения поставленной задачи следует использовать 2-процессорную ПВМ, поскольку она имеет лучшие характеристики (эффективность и загруженность) по сравнению с 4 - процессорной ПВМ. Однако улучшение указанных характеристик достигается здесь за счет увеличения числа шагов алгоритма (H₂=4), т.е. за счет увеличения времени работы ПВМ.

Пример №2.3. Требуется выполнить умножение квадратной матрицы А на вектор х:
y = A × x , т.е. y_i = S a_ij x_j , ( i = 1…n , j = 1…n )(2.6)
на ПВМ, имеющей n²процессоров.

Эта задача распадается (распараллеливается) на n независимых ветвей вычисления n скалярных произведений векторов а_iи x(см. Пример 2.2). Параллельный алгоритм решения данной задачи включает следующие этапы:
а) на первом шаге вычисляются все n² произведений вида a× x.
б) с использованием схемы сдваивания (см. табл.2.1 и табл.2.3) для операций сложения за H=log₂ n шагов вычисляются все n сумм, определяющих координаты вектора y. Процессоры используются неравномерно: на первом шаге используются все, а потом их загруженность уменьшается вдвое.

Пример №2.4. Вычислить произведение двух квадратных матриц порядка n на ПВМ, имеющей n³процессоров.

Параллельный алгоритм решения задачи сводится к n операциям умножения матрицы на вектор (см. Пример 2.3). ПВМ должна обеспечить одновременный доступ многих процессоров к одной и той же информации.Высота ПФ алгоритма h = log₂n+1, ширина ПФ равна n³.

Пример №2.5. Многие численные методы линейной алгебры, математической физики и анализа построены на основе использования рекуррентных соотношений:
x_i = S A_ij×x_i-j + b_i , ( i = 1…s; j = 1…r; A[n, n]; x[n]; b[n] ), (2.7)
где x_i – s искомых векторов размерности n; A_ij – s×r квадратных матриц; b_i – s векторов.

Используя n²r процессоров, правую часть соотношения (2.7) (для каждого i) можно вычислить за s× log₂n шагов. Соотношение (2.7) можно преобразовать к виду:
y_i = П Q_k × y₀ , ( i = 1…s; k = 1…i ), (2.8)
где каждый вектор yразмерности nr+1содержит соответствующие векторы xиb, а в состав каждой квадратной матрицы Qразмерности nr+1входят матрицы Aиз (2.5).

Согласно алгоритму сдваивания все произведения в соотношении (2.8) можно вычислить за число макрошагов, равное log₂ (s +1). При этом будет использовано s +1 макропроцессоров, выполняющих в качестве макрооперации умножение двух квадратных матриц порядка nr+1.Далее строится параллельный алгоритм вычисления векторов x_i с высотой log₂ s× log₂nr и шириной порядка (nr)²× s.Описанный алгоритм получил название алгоритма рекуррентного сдваивания.