Алгоритмы параллельных вычислений. Параллельные формы алгоритмов

Совместное исследование структур вычислительных алгоритмов и ПВМ показывает, что информационный поток, проходящий через ПРВС, можно расщепить на независимые ветви вычислений. Наличие в алгоритме большого числа независимых и однотипных вычислений позволяет существенно сократить время решения вычислительных задач.

Для реализации алгоритма вычислений на ПВМ необходимо представить его в виде последовательности групп операций. Они должны быть независимыми и обладать возможностью быть выполненными одновременно (параллельно) на функциональных устройствах ПВМ.

Представление алгоритма решения задачи в виде упорядоченных групп вычислительных операций, выполняемых в определенной последовательности, называется параллельной формой алгоритма (ПФ). Параллельность в алгоритме характеризуется числом операций в группе, которые могут выполняться одновременно.

Каждая группа операций называется ярусом ПФ, число групп – высотой H, максимальное число операций в ярусе – шириной B. Один и тот же алгоритм может иметь несколько ПФ, отличающихся как высотой, так и шириной. Высота H определяет число шагов алгоритма, а ширина B – число процессоров ПВМ, необходимых для решения задачи.

Если известна ПФ алгоритма, то его можно реализовать на ПВМпоследовательно ярус за ярусом (т.е. шаг за шагом). Если состав функциональных устройств ПВМ позволяет выполнить параллельно все операции любого яруса, то алгоритм может быть реализован за время, пропорциональное высоте ПФ.

Пример №2.1. Пусть требуется вычислить величину на 4-процессорной ПВМ:
X₂₁ = ( а₁ · а₂ + а₃ · а₄ ) · ( а₅ · а₆ + а₇ · а₈ ).

Вычисление величины X₂₁ можно осуществить несколькими способами. Различные порядки выполнения операций и различные разбиения операций на группы порождают различные ПФ. Одна из них представлена в табл. 2.1:

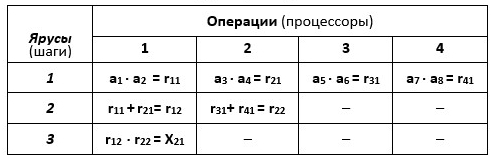
Табл. 2.1. Вычисление величины X21 на 4-процессорной ПВМ (Пример №2.1)

Здесь (и далее) r_ij -промежуточный результат i-й операции на j-м ярусе (шаге) алгоритма.

Высота ПФ (табл.2.1)H= 3, ширина B = 4. Алгоритмможет быть реализован на 4 процессорах ПВМ, способных выполнять операции сложения и умножения: сначала выполняются четыре операции умножения (ярус 1), затем две операции сложения (ярус 2) и операция умножения (ярус 3). Все четыре процессора задействованы только на первом шаге, а на других шагах часть из них простаивает. На каждом шаге алгоритма число выполняемых операций (т.е. число задействованных процессоров) уменьшается вдвое, т.е. имеет местотак называемое сдваивание операций.

Необходимо отметить, что промежуточная величина r_kl , полученная k-мпроцессором на l-м шаге, может быть использована любым процессором лишь на следующем (l +1)-м шаге алгоритма.

Основные характеристики параллельных алгоритмов. Основными характеристиками параллельных алгоритмов являются следующие.

1) Ускорение S_p показывает, во сколько раз быстрее ПВМ решает вычислительную задачу по сравнению с решением той же задачи на однопроцессорном компьютере:

S_p = T₁ / T_p , 1 ≤ S_p ≤ p, (2.1)
где: T₁ – время, необходимое для решения задачи на однопроцессорном компьютере;
T_p – то же – на ПВМ с p процессорами.

Отметим, что однопроцессорный компьютер выполняет на каждом шаге лишь одну операцию.Поскольку время решения задачи пропорционально высоте ПФ алгоритма, то для определения ускорения используется также следующая формула:
S_p = H₁ / H_p (2.2)
где: H₁ – высота ПФ, полученной при решении задачи на однопроцессорном компьютере; H_p – то же – на ПВМ с p процессорами.

2) Эффективность алгоритма определяется путем деления ускорения S_p на число процессоров р и представляет собой удельное ускорение алгоритма, достигнутое по отношению к одному процессору:
E_p = S_p / p, 1/p ≤ E_p ≤ 1. (2.3)

3) Высота алгоритма H отражает время решения задачи. Если исходная задача определяется n входными переменными, то высота алгоритма определяется соотношением:
H ³ log ₂ n. (2.4)

При решении системы линейных уравнений порядка n (т.е при числе входных переменных, равном n² )и использовании n процессоров высота алгоритма H колеблется от n² log₂ n до n² в зависимости от выбранного метода. При использовании n² процессоров h уменьшается до n log₂ n или n, а при n³ и n⁴процессоров существуют алгоритмы высотой h = log²₂n.

Задача с матрицей порядка n имеет n² входных данных, поэтому для ее решения не существует алгоритма с h меньше, чем log₂ n. Следовательно, алгоритмы с высотой порядка log²₂ n можно считать эффективными.

Общей тенденцией является уменьшение высоты параллельной формы с увеличением числа процессоров. При числе процессоров, не превосходящем n², высота обратно пропорциональны числу процессоров. При дальнейшем увеличении числа процессоров скорость снижения высоты уменьшается.

4) Загруженность процессоров Z характеризуется отношением числа выполненных алгоритмом операций к числу возможных операций, которые можно выполнить за то же время. Для параллельных алгоритмов решения задач линейной алгебры типичным является выполнение вычислений по схеме сдваивания (см. табл. 2.1), при которой быстро уменьшается число промежуточных операций. Это приводит к уменьшению загруженности процессоров, к их простаиванию и неэффективному использованию ПВМ с точки зрения быстродействия, ради которого ПВМ создается.

При числе процессоров, не превосходящем n², загруженность процессоров либо постоянна, либо является величиной порядка log₂^-1n в зависимости от используемого метода. При дальнейшем увеличении числа процессоров их загруженность падает.

5) Устойчивость U алгоритма к ошибкам округления. В процессе решения задачи на каждом шаге осуществляет округление промежуточных данных, связанное с ограниченностью разрядной сетки ПВМ. В задачах большой размерности (порядка тысяч ограничений и переменных) по мере увеличения высоты ПФ ошибки округления могут приводить к неустойчивости алгоритма и получению некорректного (неправильного) результата решения задачи. Во избежание этого явления применяются специальные методы повышения устойчивостиалгоритма к ошибкам округления, рассматриваеме, в частности, в курсе линейной алгебры.

Параллельные алгоритмы решения задач алгебры с высотами порядка log²₂n являются сильно неустойчивыми к влиянию ошибок округления и без радикального изменения они не могут быть использованы в больших ПВМ. В настоящее время не известно ни одного устойчивого метода решения алгебраических задач с полной матрицей высоты порядка log²₂n.

При числепроцессоров, не превосходящем n², устойчивость остается примерно постоянной, но при дальнейшем увеличении числапроцессоров устойчивость резко ухудшается. Устойчивость параллельных алгоритмов при большом числепроцессоров хуже устойчивости последовательных алгоритмов, реализуемых на однопроцессорных компьютерах.

6) Конфликтность алгоритмаопределяет состояние, когда два или несколько процессоров в процессе вычислений выбирают в памяти одну и ту же информацию, т.е. возникает конфликтная ситуация. Число конфликтов возрастает с увеличением числа процессоров.

Конфликтность алгоритма можно устранить путем увеличения его высоты, устанавливая для процессоров очередность доступа к информации. Технический способ устранения конфликтов состоит в использовании в ПВМ средств размножения информации.

Таким образом, основным достоинством параллельных алгоритмов(по сравнению с последовательными) является их более высокое быстродействие в связи с использованием большого числа процессоров. Но за это приходится платить ухудшением других свойств алгоритмов. Среди рассмотренных характеристик ускорение, эффективность, высота и загруженность улучшаются с увеличением числа процессоров, а остальные характеристики при этом ухудшаются.

Принципиально важно создание параллельных алгоритмов со свойствами, не уступающими свойствам последовательных алгоритмов по асимптотике итерационных процессов, числу арифметических операций, объему необходимой оперативной памяти, числу обменов с дисковой памятью и другим показателям.